043

43

2.3. Zmienne losowe typu ciągłego

skąd gęstość zmiennej losowej Y jest postaci

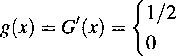
dla x e (1,3), dlax$ (1,3).

g) Mamy kolejno:

1.    Pr(X < 0) = 0, gdyż Pr(X € [0,ln3]) = 1,

2.    Pr(X< l) = (e-l)/2» 0.859141,

3.    Pr(0.5 < X < 0.7) « 0.182516,

4.    Pr(y<l)=0, gdyż Pr(y 6 [1,3]) = 1,

5.    Pr(y< 1.5) =0.25.

Zadania

Zadanie 2.3.1.

Dla jakich wartości parametrów a,b,c, funkcja

a dla x < — 1, f(x) = < b dla — 1 < x < 1, c dla x ^ 1

jest gęstością pewnej zmiennej losowej X? Zadanie 2.3.2.

Gęstość zmiennej losowej X wyraża się wzorem:

a yfx dla 0 < x < 1, 0 poza tym.

Obliczyć a, a następnie EX^k i D²X.

Zadanie 2.3.3.

Gęstość zmiennej losowej X wyraża się wzorem:

0 dla x ^ 1.

Obliczyć a, a następnie EX. Czy istnieje D²X? Zadanie 2.3.4.

Niech zmienna losowa X ma gęstość

.4cos* dla * e (—it/2,n/2), 0    dla * ^ (—zr/2, zr/2).

Obliczyć