25 (5)

Biblioteczka Opracowań Matematycznych

.fpiph,.,

³

t²-t +1 AB C

- = h + •

t(2t-\f i 2/ — 1    (2/ — 1 )²

A =

4A + 2B = 1 C-4A-B = -l A = 1

2

r = -2

_{I = 2}jj-3j^₊3j-^~ = 2ln\t\-h_n\2t-\\~ = 2\_n\x-^x²-x ₊ \

— — In|2a- — 2-s/jr¹ -x + I -1|-

2 I

159/

r sin' xdx

'l-f-cos²x

lgx -I o- = arctgt

dx=^dt

i+r

2(r-'\/x²~-x + l-l)

+c

_ r l + /^: dl f cdi r 2dl r dl

~^J, ₊ _L i+r ~ ^J{277j(i77j" J 771~ J7vT"

i+r

= ²J

di

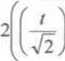
+ 1

- arctgt = 4larctg^ ~ j - arctg(tgx)+C

160/

JH* = F(x)

x, x> 0 O AT = O -x, x<0

Funkcja F(x) jest różniczkowalna w R, więc jest także różniczkowalna dla x = 0. Stąd:

F(x) =

y + C, X> O C x = 0 -- + C, x<0

lim F(x)= lim f(x)= F(o)

x-*0

lim	fx^2 1 —+ C,	= limf
x-*0*	v ^2 J	x-»0*l	2 J

= c

c,=c₅ = c

gdzie C jest dowolną stałą.

Biblioteczka Opracowań Matematycznych

Mi/ j|x-l|obr = /

x-l X >1

r(x)=(x-i|=

O x = l

-X+I X<I

F(x) =

--x + C. x>I

2 '

C x = l

Jf²

--+ x + C, jc<1

2 ¹

Ponieważ F(x) jest różniczkowalna w R. więc jest różniczkowalna w punkcie x = 1 a stąd ciągła dla x = 1. Stąd:

lim F(x)= lim f(x) = F(l)

x-*r    *-•!*

lim

x-*r

^x²

-x + C,

= lim

x-*r

f x‘

- — + x + C, 2

c,-^=c_ł+i=c

C₂=C,-1

gdzie C| jest dowolną stałą. 162/

= C

(■arcsinxi/v	[ arcsinxcfc	arcsiiur = f x = sin/	- f.
^l*-sJ	Wl-x^2(l-x^2)	dt- ,-- x -sin f l-x'-cosr/	J

tdt

M=f ć/w=</l . ^dt

dv=—— v=tgt co sr

=ttgt- J/g/t/#=ng/+lijcos| +C=arcsinr

sir/arcsior)

co/arcsiuj

+1

r|Vl-x²|

+C=

xarcsin x

•y/l-sin²(arcsinx)

+ ln

(.-X²)¹

_ xarcsinx 1. i, ₂\ ^ + C = —,,■■■    ■ + —In I -x m-C

2'

163/

'arctę

1+X*

jX* arctgxdx

arctgt t x=tgt

= jttgtdt=

u—t

du=dt

dv=tgtdt v= ^gtdt=    ^—ljdt=rgt-t

= ttgt -t² - Jtgtdt + jtdt = arctgx(tg{arctgx)) + ln|cos/| - \^(arctgxf =

= xarctgx + ln|cos(arctgx)| - ~ (arctgxf + C

-49-