2b (9)

Procedura testu istotności

Sposób weryfikacji hipotezy statystycznej składający się z następujących czynności:

> przyjęcie określonego poziomu istotności a

> sformułowanie hipotezy zerowej (H₀)

> sformułowanie hipotezy alternatywnej (//,) {w zależności od hipotezy zerowej (H₀) test może być jednostronny lub dwustronny}

> ustalenie sprawdzianu testu (statystyki) i jego wartości na podstawie dostępnych informacji o zbiorowości generalnej i próbie

> odczytanie wartości krytycznych sprawdzianu testu ( z tablic rozkładu normalnego, t-Stiidenta lub chi-kwadrat) przy danym poziomie istotności a i informacjach pochodzących z próby losowej

> ' ustalenie obszaru (krytycznego) odrzucenia (H₀) przy danym poziomie

istotności a (obszar ten może być jednostronny lub dwustronny)

> przyjęcie decyzji o odrzuceniu lub braku podstaw do odrzucenia hipotezy zerowej (//₀) {na podstawie statystyki testu z wartością krytyczną}

> porównanie wartości p z a

Test zgodności - procedura statystyczna pozwalająca na ustalenie czy można odrzucić lub nie hipotezę o hipotetycznym rozkładzie prawdopodobieństwa. Test zgodności jest oparty o rozkład chi-kwadrat.

Testy zgodności stosujemy do zmiennych losowych jak i ciągłych.

Test zgodności chi-kwadrat jest testem nieparametrycznym w rachunku strukturalnym.

Sprawdzian testu zgodności chi-kwadrat - jest to statystyka mająca rozkład chi-kwadrat o (k-p - 1) stopniach swobody.

gdzie;

>

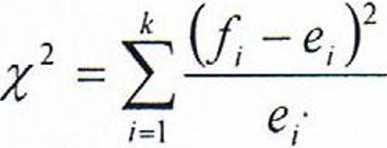
f] - obserwowana (empiryczna) częstość absolutna (liczebność) w przedziale klasowym i

e_i - spodziewana (teoretyczna) częstość absolutna (liczebność) w przedziale * i oparta na założeniu prawdziwości hipotezy zerowej (H₀)

k - liczba przedziałów klasowych (wymóg co najmniej 5 elementów w każdym przedziałów w przypadku częstości teoretycznej e_t)

(k - p - 1) - liczba stopni swobody, przy czym p liczba parametrów zbiorowości generalnej szacowana na podstawie próby (n > 30)

Hipotezę zerową testu zgodności (//₀), która brzmi, że próba pochodzi ze zbiorowości o

określonym rozkładzie teoretycznym odrzuca się, jeśli X² - xl (obszar krytyczny w rozkładzie chi-kwadrat jest zawsze prawostronny) dla danego o. i (k - p - 1) stopni swobody, bowiem p(x² >xl)=a.