CCF20090523021 tif

KARL R. POPPER

Pozwolę sobie zatem zająć się teraz samym światem 3.

Jak wspominałem w trakcie mojego pierwszego wykładu w zeszły czwartek, to, co nazywam światem 3, można scharakteryzować, najogól-i niej biorąc, jako świat wytworów ludzkiego umysłu. Do świata 3 należą stwory architektury, sztuki, literatury, muzyki, wiedzy oraz — co najistotniejsze —problemy, teorie i krytyczne dyskusje naukowe.

1 Oczywiście nazwa „świat 3” jest tylko pewną metaforą: możemy, jeśli tak się nam spodoba, wyróżnić więcej światów. Moglibyśmy, na przykład, wyróżnić świat wiedzy obiektywnej jako świat odrębny od świata sztuki; można byłoby również przeprowadzić inne rozróżnienia. Nie chciałbym wprowadzać jednak większego zamętu, niż to jest konieczne ze względu na nasze zasadnicze cele.

Otóż kiedy powiedziałem, że nazwa „świat 3” jest metaforą, nie powiedziałem o niej wszystkiego. Jest to bowiem wjakiejś mierze coś więcej niż metafora. Jest to także coś więcej niż świat wytworów umysłu. Wskazywałem pewne wątki, które się z tym wiążą w trakcie mojego pierwszego wykładu i dyskusji, ale teraz wyjaśnię to bardziej wyczerpująco.

Rozważmy to na przykładzie geometrii. Geometria jest, rzecz jasna, tworem człowieka; dysponujemy nawet pewnymi historycznymi przekazami dotyczącymi jej początków w Egipcie i w Babilonie: służyła najpierw jako narzędzie wykorzystywane do pomiaru gruntów, przypuszczalnie po to, by ułatwić szacowanie podatku gruntowego.

Idea posługiwania się wszędzie tam, gdzie to możliwe, tylko prostymi i okręgami jest również, rzecz jasna, tradycją stworzoną przez człowieka —podobnie jak idea kąta prostego. Nie jest natomiast faktem stworzonym przez człowieka, że dla każdego okręgu obowiązuje następujący sąd czy twierdzenie: wykreśl średnicę; wybierz dowolny punkt na obwodzie okręgu różny od końców tej średnicy i połącz go za pomocą linii prostych z dwoma jej końcami; te linie proste utworzą wówczas kąt prosty w owym wybranym punkcie.

Geometryczny sąd bądź twierdzenie, takie jak twierdzenie, które przed chwilą sformułowałem, nie jest na ogół przez nas wytworzone. Pojawia się j ako niezamierzona konsekwencja wynalezienia geometrii: cyrkla i okręgu,

liniału i prostej. Istnieją, naturalnie, setki takich twierdzeń, wśród których są również twierdzenia daleko głębsze. Ale wraz z każdym wyłaniają się także nowe problemy, takie jak problem, w jaki sposób dane twierdzenie udowodnić. (Dopiero gdy dowód zostanie podany, nazywamy je „twierdzeniem”— dopóki to nie nastąpi, nazywamy je „przypuszczeniem”.) To znaczy: w jaki sposób jest powiązane z innymi sądami geometrycznymi? Nasze konkretne twierdzenie wynika w istocie niemal bezpośrednio z dwóch sądów: sądu głoszącego, że suma kątów każdego trójkąta równa się dwóm kątom prostym (które tworząrazem linię prostą) — który wedle Arystotelesa ukazuje istotę trójkąta; oraz innego sądu, który głosi, że jeśli w trójkącie dwa boki są równe, to dwa kąty, które są zawarte między tymi bokami a trzecim bokiem, również są równe.

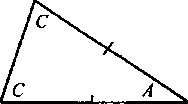
A zatem A + 2C = 2R

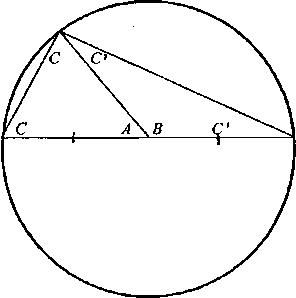
Z tego sądu oraz z sądu, że suma kątów trójkąta jest równa dwóm kątom prostym, a następnie z definicji okręgu, która głosi, że wszystkie promienie okręgu sąrówne, otrzymujemy dowód, który pewna wątpliwa interpretacja tradycji przypisuje twórcy greckiej filozofii Talesowi: A+B=2R A + 2C = 2R B = 2C /.*. C = BU

Podobnie,

A+B = 2R B + 2C'=2R l.\A=2C'

/.*. C' = A/2

/.*. C + C' = A/2 + B/2 = \R