FizykaII57201

568

568

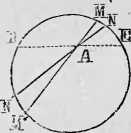
Fig. 310.

§ 83. Warunek elektrycznej równowagi i prawo elektrycznego działania. Elektryczność w stanie równowagi musi na powierzchni dobrego przewodnika mieć wszędzie takie napięcie, iżby całkowite jćj działanie na każdy wewnętrzny punkt tegoż przewodnika było = o, gdyż w przeciwnym razie nastąpiłaby tam zaraz zmiana naturalnego stanu ± E, a tern samem nowe rozwinięcie wolnej elektryczności, co się przyjętemu stanowi równowagi sprzeciwia. Z tego zaś wynika z koniecznością, że zelektryzowane cząstki ciała działają jedne na drugie nawzajem w odwrotnym stosunku kwadratów z odległości punktów przy-przyłożenia sił elektrycznych. Gdy albowiem ciałem naelektry-zowanem jest metalowa kula, otoczona złym przewodnikiem, elektryczność jej wystawia niejako warstwę jednostajnie gęstą działacza, rozpostartego na powierzchni, czyli rodzaj dętej kuli o bardzo cieniuchnych ścianach, będących siedzibą równeg > wszędzie elektrycznego napięcia, a działanie takiej kuli na każdy punkt, wewnątrz niej leżący, jest =: o. Atoli za pomocą rozumowania, w taki sam sposób, jak w § 118 T. I przeprowadzonego, nietrudno się przekonać, że to wtedy tylko jest możliwćm jeżeli wielkości działania każdej najmniejszej cząsteczki tej kulistej warstwy elektrycznej na rzeczony pnnkt wewnętrzny mają się do siebie odwrotnie, jak kwadraty z ich odległości od niego. Wszak gdy punkt A wewnątrz naelektryzowanej kuli, któ-rćj przecięcie środkowe Fig. 310 przedstawia, jest punktem w mowie będącym, a płaszczyzna przez BE przesunięta, stoi prostopadle na średnicy, przez A przechodzącej, wszystkie cząstki odcinka DME, bliższe punktu A, niż przeciwległe im względem A cząstki większego odcinka DM'E, działające nań z równą mocą w przeciwnych kierunkach, zatem znoszące się dla tego właśnie w tym punkcie nawzajem zupełnie, są też od nich mniejsze w stosunku kwadratów z odległości od tegoż punktu; gdyż wielkości każdych dwóch odpowiednich sobie cząstek elektrycznych po tej i po tamtej stronie rzeczonej płaszczyzny DAE, jak np. MN i M' N\ mają się widocznie do siebie, jak kwadraty z odległości MA i M'A, t, j. MN : M'N‘ — AM² : M'A^%-