0379

381

§ 2. Własności funkcyjne sumy szeregu

Przede wszystkim podstawiając x₀ = a, ze zbieżności jednostajnej szeregu y* ^M"⁽vZ“^,,(<ł) » a. więc i szeregu    ^ [u„(x)-u„(a)]

«—1    ir=l

oo

[patrz wniosek z 429] i ze zbieżności szeregu £ u„(a) wnioskujemy o zbieżności jedno-

N-I

CO

stajnej szeregu £ u„(x).

1

Jeżeli przez /(x) oznaczymy jego sumę, to sumą szeregu (26), gdzie x₀ jest znów dowolną wartością x z przedziału <a, ń>, jest oczywiście    . Ponieważ w zbież-

x—a

nym jednostajnie szeregu można przechodzić do granicy wyraz za wyrazem (z twierdzenia 4), więc gdy x dąży do x_Q, otrzymujemy

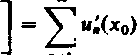
z-,,.). _Iiin    , y f,_im

X-X₀    CA _x^₀ x-x₀

K-l ^L

c.b.d.o.

Uwaga. Wszystkie twierdzenia o przejściu do granicy, całkowaniu i różniczkowaniu wyraz za wyrazem ustalają analogię między szeregami funkcyjnymi a sumami skończonej liczby funkcji. Analogia ta jest jednak ograniczoną znanymi warunkami, w których zbieżność jednostajna odgrywa zasadniczą rolę.

436. Przeniesienie wyników na ciągi. Ciekawe będzie przeniesienie otrzymanych wyników na przypadek ciągów funkcji. Pozwoli to nam na wyraźne ustalenie związku rozpatrywanych zagadnień z ogólnym zagadnieniem zmiany kolejności przejść granicznych, które odgrywa tak ważną rolę w całej analizie. Oprócz tego wytyczymy drogę w kierunku uogólnienia tych wyników.

Znów więc przyporządkowujemy wzajemnie ciąg funkcji (1) i szereg funkcyjny (3) związane zależnościami

/»(*) =    «*(*)    (« = 1,2, 3,...)

k-l

łub równoważnymi z nimi zależnościami

«i(x) = fi(x), u„(x) = /_B(x)-/„-,(x) (n = 1, 2, 3,...) .

Funkcja graniczna ciągu jest równa sumie odpowiedniego szeregu. Zbieżność jednostajna może zachodzić tylko jednocześnie dla ciągu i dla szeregu.

I. Rozpatrzmy najpierw zagadnienie znajdowania granicy tej funkcji granicznej. Niech zbiór = {x}, w którym wszystkie rozpatrywane funkcje są określone, ma punkt skupienia a. Twierdzenie 4 z ustępu 433 otrzyma teraz postać następującą:

Twierdzenie 4*. Jeżeli funkcje /„(x) mają granice (28)    lim/_B(x) = /(x) (x z 90