0387

389

§ 2. Własności funkcyjne sumy szeregu

A więc rozwinięcie funkcji f(x, y) (jeżeli jest tylko możliwe) musi mieć postać

l,*-0

d^tĄ*f(x₀,y₀)

dx^tdy^k

(x-x₀)^t(y-y₀yⁱ.

Ten szereg nazywamy również szeregiem Taylora. Jest on w sposób naturalny związany ze wzorem Taylora, o którym mówiliśmy w ustępie 195. Gdy takie rozwinięcie funkcji f{x,y) istnieje, to funkcję nazywamy analityczną w punkcie (x₀> To)-

§ 3. Zastosowania

439. Przykłady na ciągłość sumy szeregu I przejście do granicy wyraz za wyrazem. 1) Zbadać ciągłość sumy szeregu

*^(X) S n’+x²it^l

przy założeniu, że pq>0 i jeden z tych wskaźników jest > 1 (co gwarantuje zbieżność szeregu dla wszystkich wartości x). Oczywiście wystarczy, jeżeli ograniczymy się do x nieujemnych.

Jeżelip>\, to dla x<x₀ (*o jest dowolną liczbą dodatnią) mąjorantą szeregu będzie szereg zbieżny

00

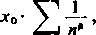
n-1

a więc z kryterium Weierstrassa wynika, że szereg jest zbieżny jednostajnie i jego suma w przedziale <0, *₀> jest ciągła. Z uwagi na dowolność x₀ suma jest ciągła w całym przedziale <0, + oo).

Jeżeli natomiast p< 1, lecz ?>1, to gdy dla jc>0 napiszemy szereg w postaci

<X>

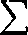
R> 1

1

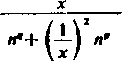
stwierdzamy jak poprzednio, że jego suma jest ciągła dla wszystkich x>0. Tak więc pozostaje do zbadania tylko punkt x — 0.

Stosując metody rachunku różniczkowego można wykazać, że n-ty wyraz szeregu osiąga największą wartość dla x =    i wartość ta wynosi

Jeżeli p + q>2, to mąjorantą naszego szeregu jest szereg zbieżny

CO

1VJL

2 Z_i n^l,+,)/1 ’

n— i

co gwarantuje ciągłość funkcji f{x) dla wszystkich x z punktem x = 0 włącznie.

Pozostaje otwarta kwestia ciągłości f{x) dla x = 0 w przypadku, gdy p<l,^>l, lecz p+q< 2. Zobaczymy dalej [491, 13)], że przy tych założeniach funkcja /(x) jest nieciągła w punkcie x = 0.

2) Rozpatrzmy szereg Dirichleta [385, 3)]

CO

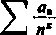
n— 1