0383

385

§ 2. Własności funkcyjne sumy szeregu

Twierdzenie to, ustalające jednoznaczność rozwinięcia funkcji w szereg potęgowy jest często stosowane. Korzystając z niego można na przykład udowodnić natychmiast, że rozwinięcie funkcji parzystej (nieparzystej) w szereg potęgowy postaci (31) może zawierać wyłącznie parzyste (nieparzyste) potęgi x.

Rozpatrzmy teraz bardziej subtelne zagadnienie zachowania się szeregu w pobliżu jednego z końców x — ±R przedziału zbieżności (przyjmując odtąd, że jest to przedział skończony). Możemy ograniczyć się do prawego końca x = R, gdyż wszystko co o nim powiemy odnosi się także do przypadku lewego końca x = — R.

Przede wszystkim oczywiste jest, że:

4° Jeżeli szereg potęgowy (31) jest rozbieżny na końcu x = R jego przedziału zbieżności, to zbieżność szeregu w przedziale <0, R) nie może być jednostajna.

Rzeczywiście, gdyby miała miejsce zbieżność jednostajna, to można by, korzystając z twierdzenia 3, przejść do granicy wyraz za wyrazem dla x -* R—0 i stwierdzić tym samym zbieżność szeregu granic 00

^ a„Rⁿ = a₀+ai R + a₂ R²+ ... +a_n Rⁿ+ ... ,

«*= 0

wbrew założeniu.

Zachodzi także następujące, w pewnym sensie odwrotne twierdzenie:

5° Jeżeli szereg potęgowy (31) jest zbieżny również dla x — R (niekoniecznie bezwzględnie), to zbieżność szeregu jest jednostajna w całym przedziale <0, Rj.

Rzeczywiście, jeżeli szereg (31) przedstawimy w postaci

00

a_n xⁿ

00

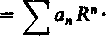
n=0

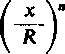
(0 < X < R) ,

CO

to żądany wniosek wynika bezpośrednio z kryterium Abela, ponieważ szereg £ a„Rⁿ

n~0

jest zbieżny, a czynniki- (x/R)" tworzą ciąg monotoniczny i jednostajnie ograniczony.

Udowodnione twierdzenie pozwala na zastosowanie twierdzenia 1 do całego przedziału <0, R>. Tak więc jako uzupełnienie twierdzenia 2° o ciągłości sumy szeregu potęgowego w przedziale otwartym (—R,R) otrzymaliśmy nowe twierdzenie (sformułowane przez Abela) (*):

6° Twierdzenie Abela. Jeżeli szereg potęgowy (31) jest zbieżny dla x — R, to jego suma jest ciągła (oczywiście lewostronnie) również dla tej wartości x, tzn.

CO

-s

a.R".

lim y¹ a_n xⁿ o

o

Twierdzenie Abela ma ważne zastosowania.

(') Inny dowód tego twierdzenia (przy założeniu R = 1) podaliśmy w ustępie 418 w związku z zagadnieniem regularności metody Poissona-Abela sumowania szeregów rozbieżnych.

25 Rflphun«>1r rA*n1r%lrnwv