0377

379

§ 2. Własności funkcyjne sumy szeregu

Twierdzenie 7. Niech funkcje u„(x) (n = 1, 2, 3, ...) będą określone iv przedziale SC = = <a, bj i mają w tym przedziale ciągle pochodne u'_n(x). Jeżeli nie tylko szereg (3) jest zbieżny, lecz także szereg utworzony z pochodnych

00

(24)    ^ufx) = uKx) + u£(x)+ ... +u,i(x)+ ...,

n=l

jest zbieżny jednostajnie w tym przedziale, to suma f\x) szeregu (3) ma w 9C pochodną i

(25)    /'« =    •

ir=l

Dowód. Oznaczymy przez /*(x) sumę szeregu (24). Z twierdzenia 1 wynika, że jest to funkcja ciągła zmiennej x. Korzystając teraz z twierdzenia 5 scałkujemy szereg (24) wyraz za wyrazem w przedziale od a do dowolnej wartości x z SC. Otrzymujemy

ff*(t)dt    =    £/ u Ht)dt,

a    »=1 a

x

lecz oczywiście fu_n (f) dt = u_n(x) — ufa), więc

a

ff*(t) dt = ^ [«»(*) —n„(a)]    =    ^ «.(*)-    ^ ufa) = f(x)-f(a).

o    ii= 1    ir=l    n=l

Przekształcenie to jest dopuszczalne, gdyż z góry wiadomo, że szeregi £ufx) i 2^M»(^fl) są zbieżne [patrz 364, 4°]. Ponieważ całka po lewej stronie, wobec ciągłości funkcji podcałkowej, ma pochodną równą/*(x) [305, 12°] przeto taką samą pochodną ma funkcja /(x), która różni się od tej całki tylko o stałą.

Równość (25) można napisać (korzystając z oznaczenia Cauchy’ego pochodnej) w postaci

00    CO

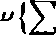
V Du„(x).

“«(*)} =

n=l    n=l

Tak więc, przy przyjętych założeniach, pochodna sumy szeregu jest równa sumie szeregu utworzonego z pochodnych jego wyrazów lub inaczej: dopuszczalne jest różniczkowanie szeregu wyraz za wyrazem.

Rozpatrzmy szeregi

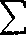
00 n= l

oraz

-^-ln(l + x²)+ ^ Ty^ln (1+n²x²) —    ¹ ln [l+(n-l)²x²]

n«2 L

Pierwszy z nich jest równy 0 dla x = 0 i jest równy 1 w pozostałych punktach, a suma drugiego jest wszędzie równa 0. Różniczkując je wyraz za wyrazem otrzymamy znane nam już szeregi (15) [431] zbieżne w całym przedziale <0, 1> do 0, lecz obydwa niejednostajnie. W pierwszym przypadku szereg pochodnych jest zbieżny także w punkcie x = 0,