0458

460

XII. Ciągi i szeregi funkcyjne

sumy częściowe szeregu rozbieżnego mogą być doskonałymi przybliżeniami liczby, która w tym czy innym sensie zrodziła ten szereg. Aby czytelnik mógł z góry wyczuć praktyczną możliwość stosowania szeregów w rachunkach przybliżonych, wystarczy wspomnieć, że z metod tych korzystają zwykle astronomowie przy obliczeniach położenia ciał niebieskich, a dokładność otrzymanych wyników jest całkowicie zadowalająca.

Postaramy się najpierw wyjaśnić potrzebne nam idee na prostych przykładach.

1) Rozpatrzmy szereg logarytmiczny

(1)    x— — +    — ... +(-«■-*    +(-1)'^- + •••

2    3    n    n+l

Dobrze wiadomo [405], że szereg ten jest zbieżny i przedstawia funkcję ln (l+x) tylko dla —l<r<l, Poza tym przedziałem (na przykład dla x> 1) szereg ten jest rozbieżny i nie ma sumy. Jednakże nawet dla wartości x>l funkcja ln (l+x) jest nadal związana z sumami częściowymi tego szeregu rozbieżnego. A mianowicie, na mocy wzoru Taylora jest

ln (l + x) = x- 4?- +■ — ~ ... +(-l)-¹ — +!•„(*),

2    3    n

gdzie resztę r„(x) możemy wziąć na przykład w postaci Lagrange’a [126]

r,(x)

1

(i+e₁x>"+¹

■(-i)"

n+l

X**¹

n+l

(0 < 0, 0i < 1).

Okazuje się, że reszta jest co do bezwzględnej wartości mniejsza niż pierwszy odrzucony wyraz szeregu i ma ten sam znak (tak samo jak w przypadku zbieżnego szeregu naprzemiennego). Tak więc, jeżeli wartość ln (l+x), dla x>l zastąpimy przez sumę częściową szeregu rozbieżnego (1), to otrzymamy wygodne oszacowanie błędu (znamy nawet jego znak). Wystarczy to już, by można było użyć tej sumy częściowej do obliczenia przybliżonej wartości ln(l+x).

Oczywiście, jeżeli 0<x<l, to dla n dążącego do nieskończoności błąd dąży do 0, a przy ustalonym n i x -* 0 mamy nawet

—*■ 0,    tzn. r„(x) = o (x"),

x“

czyli że błąd jest w porównaniu z x nieskończenie małą rzędu wyższego niż n. Dla dowolnego ustalonego x>l wyrażenie dające oszacowanie samo rośnie do nieskończoności wraz z n. A więc nie może tu być mowy o tym, żeby dla danego x uczynić błąd dowolnie małym przez odpowiedni wybór n. Jednakże, jak widać z samego oszacowania,

k.(x)l <

x"⁺¹

n+l

dla x dostatecznie bliskich 1 błąd może być dowolnie mały. Gdy x będzie ustalone, lecz bliskie 1, wówczas wyrazy szeregu (1), nawet dla x>l, będą najpierw malały co do wartości bezwzględnej, a mianowicie dopóki będzie

x"⁺¹ . x" n+l ’ n

n

n+l

x < 1

lub n <-,

x—1

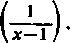
potem zaś dopiero zaczną rosnąć.

Nąjwygodniej obciąć szereg na wyrazie o wskaźniku n = E

Otrzymamy w ten sposób dla danego x najlepsze przybliżenie liczby ln (1 +x).

W przedstawionym przykładzie rozpatrywany szereg (1) był jednak zbieżny dla -1 <x< 1. Przykład drugi będzie bardziej pouczający z tego względu, że będziemy tu rozpatrywali szereg wszędzie rozbieżny.