new 49

100 6. Obliczenia gwintów

q(N) — .    — cosh mN = Qm ctgh mN.    (6.33)

sinhmN

Gdyby nakrętka była nieskończenie wysoka, zachodziłyby równania 'lim ctgh mN — 1 oraz lim q(N) = Qm dla N -> oo.

Przyjęcie nakrętki o skończonej wysokości prowadzi do zwiększenia obciążenia na dolnym zwoju. Obliczmy przykładowo jaką wysokość powinna mieć nakrętka aby wzrost obciążenia dolnego zwoju nie przekroczył 10% obciążenia, jakie istniałoby w przypadku nakrętki nieskończenie wysokiej. Dla ctgh mN = 1,1 z tablic funkcji hyperbolicznych odnajdziemy wartość argumentu mN — 1,52. Można zapisać to w postaci (patrz

N t? N

wzór 6.28) mN = md = p d — =1,52 lub

-f-T-r-

Liczbę zwojów gwintu nakrętki można określić ze wzoru

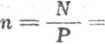
1,52 & ’

(6.35)

gdzie »'> określa się z wykresu przedstawionego na rys. 6.6.

N

Na rysunkach 6.8 i 6.9 przedstawiono wykresy — i n określonych

d

wzorami (6.34) i (6.35). Z wykresów tych wynika, że ze wzrostem — liczba zwojów n rośnie, natomiast stosunek wysokości nakrętki do śred-

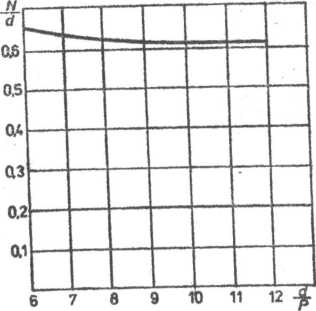
Rys. 6.8. Względna wysokość nakrętki — w zależności od-i ^K1 d    P

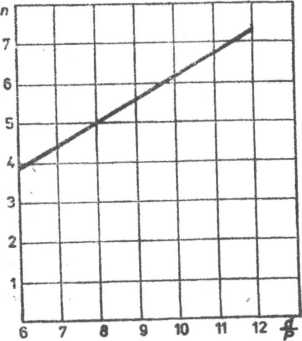
Rys. 6.9. Liczba zwojów nakrętki n w zależności od Ą-

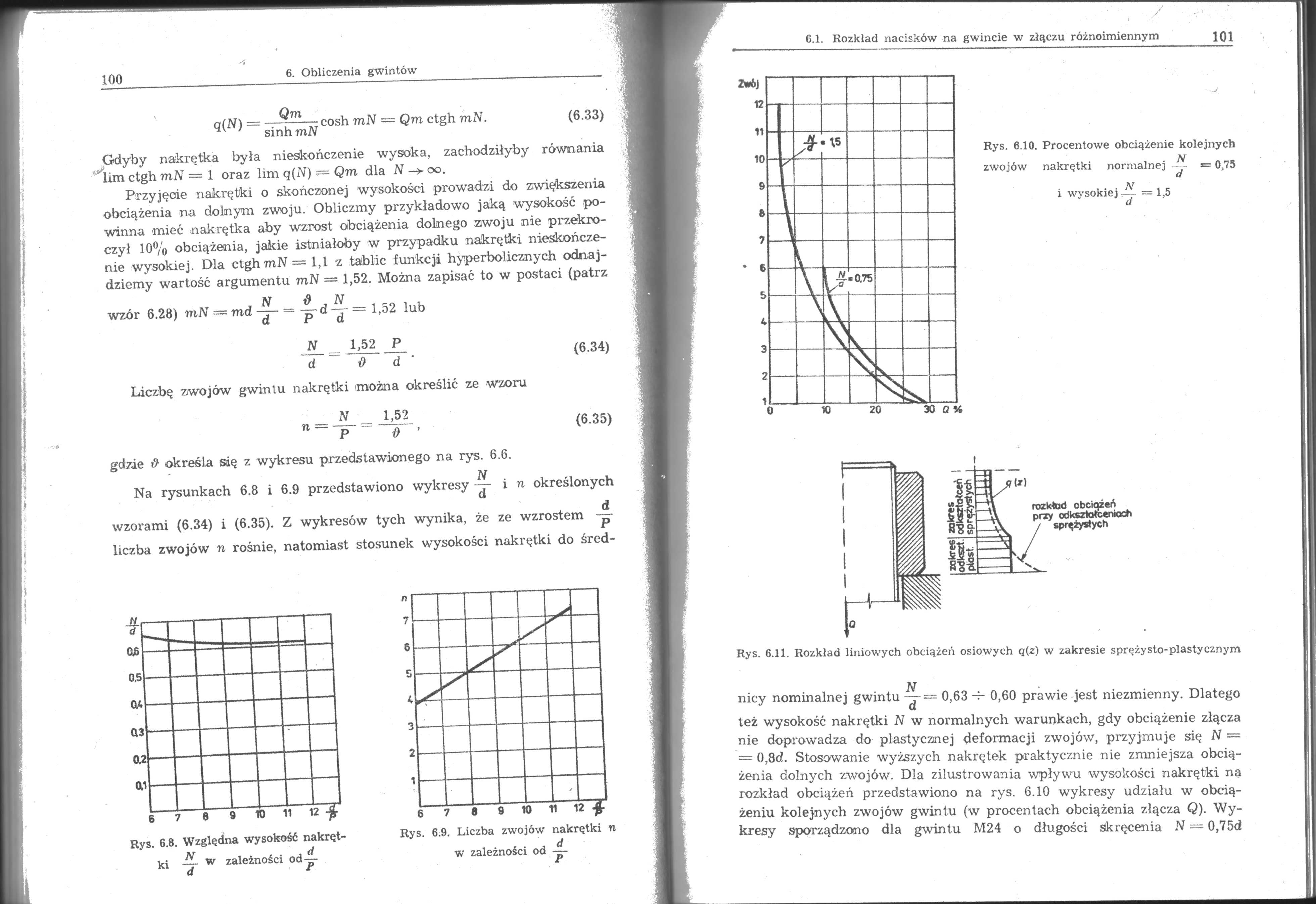
2"&j 12 11 10 9 6 7 ♦ $ 5 L 3 2 1									Rys. 6.10. Procentowe obciążenie kolejnych zwojów nakrętki normalnej = 0,75 d N i wysokie):— =1,5 d
			4-	t5
				l It 1yG	* 0.75
l	10 20 30 a H

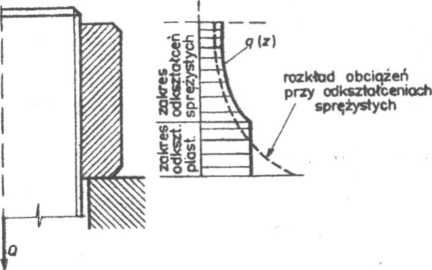
Rys. 6.11. Rozkład liniowych obciążeń osiowych q(z) w zakresie sprężysto-plastycznym

N

nicy nominalnej gwintu — = 0,63 -i- 0,60 prawie jest niezmienny. Dlatego

też wysokość nakrętki N w normalnych warunkach, gdy obciążenie złącza nie doprowadza do plastycznej deformacji zwojów, przyjmuje się N = — 0,8d. Stosowanie wyższych nakrętek praktycznie nie zmniejsza obciążenia dolnych zwojów. Dla zilustrowania wpływu wysokości nakrętki na rozkład obciążeń przedstawiono na rys. 6.10 wykresy udziału w obciążeniu kolejnych zwojów gwintu (w procentach obciążenia złącza Q). Wykresy sporządzono dla gwintu M24 o długości skręcenia N — 0,75d