068 069

68

tt/l

I

		M	«	11	u
	I	%	%	%
	1	%	y.	y«	y.
	U	M	n	n	i
1	0	\	i	i	i
1	1	i	i	i	i
l	1	i	$	i	•
3	t	i	j	i	i

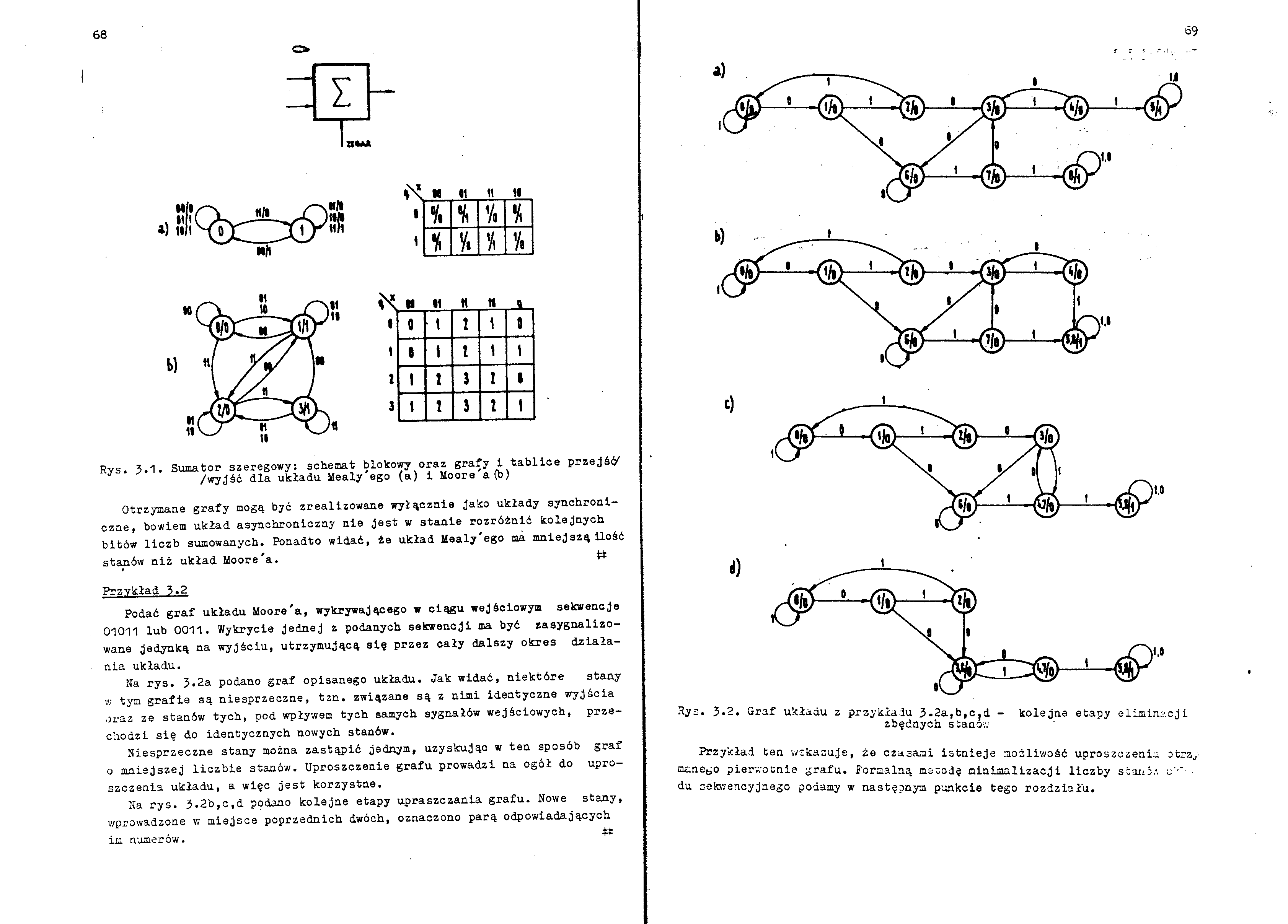
Rys. 3.1. Sumator szeregowy: schemat blokowy oraz grafy i tablice przejść /wyjść dla układu Mealy'ego (a) i Moore'a{b)

Otrzymane grafy mogą być zrealizowane wyłącznie jako układy synchroniczne, bowiem układ asynchroniczny nie jest w stanie rozróżnić kolejnych bitów liczb sumowanych. Ponadto widać, że układ Mealy'ego ma mniejszą ilość

stanów niż układ Moore'a.    #

«

Przykład 3.2

Podać graf układu Moore'a, wykrywającego w ciągu wejściowym sekwencje 01011 lub 0011. Wykrycie jednej z podanych sekwencji ma być zasygnalizowane jedynką na wyjściu, utrzymującą się przez cały dalszy okres działania układu.

Na rys. 3*2a podano graf opisanego układu. Jak widać, niektóre stany w tym grafie są niesprzeczne, tzn. związane są z nimi identyczne wyjścia oraz ze stanów tych, pod wpływem tych samych sygnałów wejściowych, przechodzi się do identycznych nowych stanów.

Niesprzeczne stany można zastąpić jednym, uzyskując w ten sposób graf o mniejszej liczbie stanów. Uproszczenie grafu prowadzi na ogół do uproszczenia układu, a więc jest korzystne.

Na rys. 3*2b,c,d podano kolejne etapy upraszczania grafu. Nowe stany, wprowadzone w miejsce poprzednich dwóch, oznaczono parą odpowiadających im numerów.    ł*

Hys. 3.2. Graf układu z przykładu 3.2a,b,c,d - kolejne etapy eliminacji

zbędnych s tanów

Przykład ten wskazuje, że czasami istnieje możliwość uproszczenia otrz, manebO pierwotnie srafu. Formalną metodę minimalizacji liczby stan 3a u'-' ' du sekwencyjnego podamy w następnym punkcie tego rozdziału.