296 (9)

11. CIĄGŁOŚĆ I POCHODNA FUNKCJI

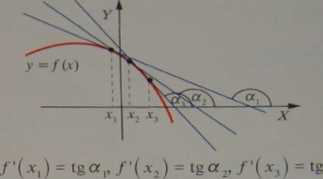
a,, a₂, a₃ - kąty rozwarte /'(jc.) < 0 dla /n; i - 1, 2,3

11. Ciqgłoi< I pochodna funkcji

11.3. POCHODNA A MONOTONICZNOŚĆ I EKSTREMUM

Rachunek pochodnych to część rachunku różniczkowego (dział matematyki) zajmującego się związkami międz> funkcjami (/) i ich pochodnymi (/')• Otóż własności pochodnej funkcji determinują j pewne własności funkcji (funkcji danej).

11.3.1. Uwagi wstępne

Wartość pochodnej funkcji w punkcie jest związana z nachyleniem stycznej do wykresu w tym punkcie do OX* (por. 11.2.1el):

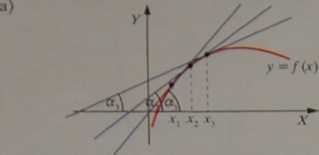
/'(*,) = tga,, /'(*₂) = tga₂, /'(*j) = tga₃ a,, a j, a₃- kąty ostre /•(*,)> Odia//;/= 1,2,3

Rysunki sugerują związek pochodnej /' z monotonicznością funkcji (por. 2.1.5d., 2.1.6d. i 2.5.2f.)

b)

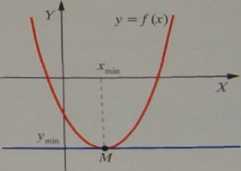
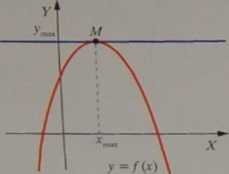
/'(O ^{= t}8°' ^{= 0}

(styczna w MII do OX) (styczna w MII do OX)

Rysunki sugerują związek pochodnej z ekstremum funkcji (por. 2.1.5e., 2.1.6c. i 2.5.2h.)

Euklides (365-300 p.n.e.) — podobnie jak inni wielcy geometrzy greccy, zajmował się astronomią, optyką i teorią muzyki, a swoje rozważania przedstawi! w dziełach: Zjawiska (elementarna astronomia sferyczna), Optyka (nauka o perspektywie) i Przekrój kanonu (teoria muzyki).

Jego głębokie zainteresowanie budziły sprawy logicznych podstaw matematyki. W książce Dane Euklides zajmował się problemem minimalnej liczby danych wielkości niezbędnej do tego, by dane zadanie było określone.

Elementy Euklidesa — ta księga powstała ponad dwa tysiące lat temu, ale nie straciła wciąż swego znaczenia. Przedstawiony w niej system geometrii euklidesowej obecnie jeszcze jest przedmiotem nauki we wszystkich szkołach świata i stanowi podstawę niemal całej praktycznej działalności ludzi.

Na geometrii Euklidesa opiera się mechanika klasyczna. Tfccść Elementów bynajmniej nie wyczerpuje geometrii elementarnej - przedstawia ona podstawy całej antycznej matematyki.