414 (6)

414 Podstawy nawigacji morskiej

stąd

(19.24)

h₀ = h_HH/?(sin 7_t)

Przykład:

Obliczyć wysokość pływu w odstępach co godzinę dla skoku 2.0 m, gdy: h_HW= 2,2 m. h_LW = 0,2 m Dane należy podstawić do wzoru:

h_a = h*w ~ ^R' s/n²/

Ze wzoru wynika, że dla

f, = 1^h (15°) h„ =2,2-2-0,066 = 2,2-0,13 = 2,07 fj = 2^h    (30°)    h_t2    = 2,2 -    2 • 0.25 = 2,2 - 0,5 = 1.7

h = 3^h    (45°)    h,₃    = 2.2 - 2 • 0,5 = 2,2 - 1,0 = 1,05

ł„ = 4^h    (60°)    h._Ą    = 2.2 - 2 • 0,75 = 2.2 - 1,5 = 0,7

t_s = 5^h    (75°)    h,_s    = 2,2 -    2 • 0,93 = 2,2- 1,86 = 0.34

t_e = 6^h    (90°):    h_t6    =    2.2    -    2    •    1 = 2.2 - 2.0 = 0,2

Wartości poprawek dla czasu I można określić zarówno przed momentem wody wysokiej, jak i po

19.9.3. Uproszczona metoda obliczania wysokości pływu półdobowego

Wysokość pływu półdobowego oblicza się metodą aproksymacji wysokości pływu na dowolny moment i_x.

Obliczanie wysokości pływu może być realizowane metodą analityczną, korzystając z zależności:

(I9.25)

Wzór ten może być stosowany przy założeniu, że pływ ma charakter cosinuso-idalny. Zatem dalszy proces obliczeń jest następujący:

Wartość C oblicza się wzorem:

(I9.26)

C - F(huw - hi u )

gdzie:

hui ~ wysokość wody niskiej,

////ii wysokość wody wysokiej, przy czym:

hf{w — /// n— skok — R

Współczynnik F przedstawia się następująco:

F = 1 - cos

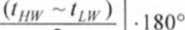
(19.27)