68 (223)

144 .:    : illtilfa:. .; ‘'.tli *•*,»•-.Jjj; • .... Punkty osobliwe i residua

) Zadanie 9.2

Znaleźć rozwinięcie funkcji /(z) w szereg Laurenta we wskazanym pierścieniu P:

a)    ^ ⁼ z(l'-"z) ’ ^P = {^z £ ^{C A} <\^z\< °°}i

^b)    f(^z) = -77“-\ > P={zGC:0<|z-l|<l>;

z(l - z)

^{C) /(g)=}(x-lKz+3)^ł    € C: 4 < lzr-t-31 < oo};

^d)    = (TT^T3)- P={*6C:2<W<3);

*

e)    /(z) = (z² + 2z)e' , P = {z € C: 0 < |z| < cx>};

l

f*) /(z) = ze"¹ , P = {z € C : 0 < |z - 1| < oo) .

Wskazówka do f*). Wykorzystać równość z — (z — 1) + 1.

Zadanie 9.3

Określić rodzaj punktów osobliwych odosobnionych podanych funkcji. W przypadku biegunów zbadać ich krotność:

sin z    ....    Z

a) /(z) =

z*+ r

d) /(z) = z tg z;

*>)/(*) = !& ^c)^) =

sin z

² 1 e)/(z) = --ri f) f(z) = zsm

g) /(*) =

1

1-1

z(cosz — 1)

—Ty h)/(z) = —i

i*) /(*) = I

e^z - 1

e‘ - 1

Odpowiedzi i wskazówki

1

z — 2

1

9.1 a) P= {z€ C. |*| >2), /(*) =

b) /> = {z e C: 1 < |«| < 2}, /(z) =    + 7+7’ ^c*) ^p - ^{z e C: 1 < ^M K 21

,, . Z² _ 1__1_

4 — 2z z z²(z — 1)

9.2 a) /(z) = - ^ ^{b) /(Z) =} “7^7 ⁺ £⁽“^ir(Z “ ^ir;

3 ■ 2"

o/M=-₇ij₊f;_f7^_;rld⁾/⁽.⁾=-|+g a«.

i    ” r | 4-2«(ⁿ + ²)1»".

e) /(z)==z² + (2 + ,)z + (-i + 2,) + ^^L-77T2)!7^:    '

Dziesiąty tydzień - przykłady

145

oo

n /(*) = (*-i) + ² + Et^

„ _ i '

n + 2

(n+ 1 )!(z — 1)"'

9.3 a) z — i, z — —i, bieguny jednokrotne; b) z = k, z = — x, punkty pozornie osobliwe; c) z — 0, punkt pozornie osobliwy, z = kx, gdzie Jt € Z \ {0}, bieguny jednokrotne;

z = 2kx, gdzie k € Z\ {0}, bieguny jednokrotne; f) z = 0, punkt istotnie osobliwy; g) z = 0, biegun trzykrotny, z = 2kx, gdzie k € Z \ {0}, bieguny dwukrotne; h) z = 1,

punkt istotnie osobliwy, z = 2kx, gdzie k 6 Z, bieguny jednokrotne; i*) z = ——:, gdzie

2kxt

k 6 Z\ {0}, bieguny jednokrotne.

Dziesiąty tydzień

Przykłady

Podać przykłady funkcji, dla których z₀ = 0 jest:

a)    punktem pozornie osobliwym;

b)    biegunem dwukrotnym;

c)    punktem istotnie osobliwym,

przy czym w każdym przypadku reso/(z) = 0. Czy można podać taki przykład, jeśli punkt ten jest biegunem jednokrotnym?

Rozwiązanie

a) Jeśli punkt z₀ = 0 jest pozornie osobliwy, to zawsze reso/(z) = 0 bo część osobliwa rozwinięcia funkcji w szereg Laurenta w otoczeniu pierścieniowym tego punktu redukuje

e^x — 1

się do zera. Na przykład dla funkcji f(z) = - punkt zo = 0 jest pozornie osobliwy,

gdyż

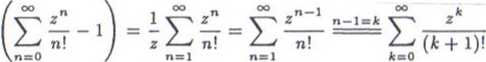
dla 0 < |z| < oo oraz reso/(z) = 0.

b) Najprostszym przykładem jest funkcja /(z) = -i-. Wyrażenie -Jj jest zarazem rozwi-

nięciem tej funkcji w szereg Laurenta dla 0 < |z| < oo. Współczynnik c_i tego rozwinięcia jest równy 0.

c) Na przykład dla funkcji /(z) = sin ~ mamy

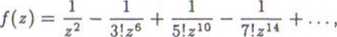
dla 0 < |z| < oo, więc C-i = 0.

Jeśli punkt zo = 0 jest biegunem jednokrotnym funkcji /(z), to z samej definicji współczynnik c_i rozwinięcia tej funkcji w szereg Laurenta w sąsiedztwie tego punktu jest różny od zera, a więc dla bieguna jednokrotnego residuum jest zawsze różne od zera.