IMAG0147 (8)

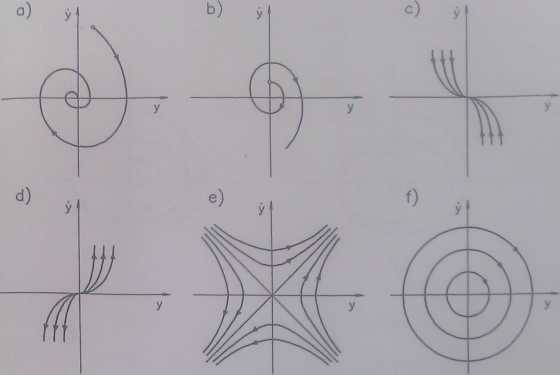
jR.ys.2- Punkty osobliwe y = 0, y = 0: a) ognisko stabilne, b) ognisko niestabilne, c) węzeł jstabilny, d) węzeł niestabilny, e) siodło (niestabilny), f) środek (stabilny)

Dla układów liniowych istnieje tylko jeden punkt równowagi o współrzędnych:

y = 0,    y = 0.

[Układy nieliniowe mogą mieć więcej punktów równowagi, a mianowicie tyle, ile jest pierwiastków [równania:

= o.

P(y,y)

Kolejną szczególną cechą układów nieliniowych jest możliwość występowania tzw. cykli ■granicznych. Występują one wtedy, gdy krzywa fazowa nie dochodzi do punktu równowagi, lecz przechodzi w krzywą zamkniętą otaczającą ten punkt. Fizycznie odpowiada to stanowi, w którym ■poszczególne fazy ruchu powtarzają się cyklicznie. Występuje zjawisko nie tłumionych drgań ■układu wokół punktu równowagi. Przykłady wykresów fazowych z cyklami granicznymi pokazano