Ch koordynacyjna II (1)

2009-01-12

Tak jak w przypadku sferycznego pola i tutaj wszystkie orbitale d podniosą swoją energię w odniesieniu do wolnego jonu ze względu na odpychanie związane z ładunkami ujemnymi.

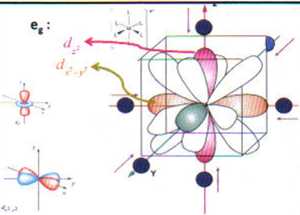
^ Należy jednak zaznaczyć jak to widać z rysunku, że nie wszystkie orbitale będą dotknięte tym oddziaływaniem w jednakowym stopniu.

¹ ❖ Orbitale leżące wzdłuż osi (d/1 d²-²) będą dużo silniej odpychane aniżeli orbitale z płatami skierowanymi pomiędzy osie (d^, d_Kl i d_yt ).

*> Stąd orbitale (/rozdzielają się na dwa zestawy tzn. orbitale o wyższej energii d*I d*-_y* niż pozostałe trzy.

♦> Podział na te dwie grupy wynika z właściwości symetrii orbitali d w obrębie oktaedrycznego otoczenia, co możemy potwierdzić z tabeli poprzez odniesienie do reprezentacji grup dla grupy punktowej O_h.

Zestaw orbitali d w oktaedrycznym polu wytworzonym przez sześć ligandów. Orbitale e_g są pokolorowane a orbitale t_2g są białe. Torus orbitalu d² został pominięty dla przejrzystości rysunku.

Zapis zwyczajowy tych dwóch nowych grup orbitali także symbolizuje te właściwości symetrii: o t_2f dla zestawu potrójnie zdegenerowanego i o e_gdla podwójnie zdegenerowanej pary a małe literki odnoszą się do symetrii orbitali.

3d

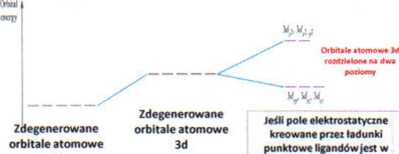
Jon Me"* i sześć ligandów L nieskończonej odległości od siebie

Jeśli pole elektrostatyczne kreowane prze punktowe ładunki ligandów jest ■ sferyczne, energie orbitali d ulegają podwyższeniu

oktaedrze, to energia elektronów orbitali 3d, które są skierowane dokładnie w .kierunku punktowego ładunku Uganda ulegają podwyższeniu w porównaniu do struktury sferycznej, podczas gdy energie orbitali nie skierowanych bezpośrednio w kierunku ładunków punktowych liganda ulegają obniżeniu.

Teoria pola krystalicznego jest modelem elektrostatycznym, który zakłada, źe orbitale d w kompleksie metalu są zdegenerowane. Sposób rozczepienia orbitali d zależy od pola kryształu a to jest uzależnione od rozłożenia i rodzaju liganda.

Ort»ul

«w*y

“7--«,    *0    * ^iilkl

-i----om.,- in,

xy xi fi

Oznaczenie O i q tq wielkościami pochodzącymi z matematycznego wzoru w elektrostatycznym modelu. Zależą one od ładunku fonu metalu, radialnej dystrybucji elektronów walencyjnych d i odległości metal-ligond. Współczynnik 10 w 10Dq pojawia się w układzie jednego elektronu w polu elektrostatycznymo oktaedtycznej symetrii.

OiMmI	—--rt -0.AA.rt ■		Zaleta teorii pola krystalicznego: > można wartość wyznaczyć z danych spektroskopowych.
	^J---•>. -0.<A - -4/>a Jv rf. *
>    Separacje energii pomiędzy nimi wynosi A^.,. lub 10Dq. >    Całkowita stabilizacja orbitali t7g jest = całkowitej destabilizacji zestawu eg. r Stąd zestaw orbitali et podnosi się o wartość 0,60^ w stosunku do środka „ciężkości" (-) podczas gdy zestaw orbitali t,g obniża się o wartość 0,40^,			kompleks d^1 [Ti(H20)6]^3* dla którego stan podstawowy może być przedstawiony za pomocą poniższego diagramu: 22Ti ls^2/2s^22p6/3s^23p^63d^2/4s^2
Na rysunku tym różnica ta pokazana jest również jako różnica energii w terminach 10Dq. Obie notacje tzn. i l0Dq są powszechnie stosowane aczkolwiek w niniejszych rozważaniach będziemy preferować zapis . Notacja Dq ma swój początek związany z teorią pola krystalicznego natomiast pochodzenie zapisu odnosi się do wartości eksperymentalnych. Stabilizacja i destabilizacja zastawów t2(i eE jest podawana w zapisie . Wielkość A,*, jest wyznaczona poprzez siłę pola krystalicznego a dwie skrajności nazywane są słabym i silnym polem			1—22Ti^3ł ls^2/2s^22p6/3s^23p^63d‘/4s° _ _ eg “1“ “ ~ ^tj‘
^ (słabe pole) < A0„ (silne pole)

2