Ch koordynacyjna II (3)

2009-01-12

itmąfia atatBMtsw# w potu toysjajteanym:

W^ftKMUD & ntete»    tttWrdgWkMOt^

Efekt różnej ilości elektronów okupujących orbitale cl w polu oktaedrycznym. dla układu ci'    stan podstawowy odpowiada konfiguracji f ,_f,

— — e,    —.

f --«« I -0,4^    -

o tj*

•£ — — •» *«-•«»

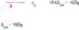
W odniesieniu do środka mamy tutaj energię stabilizacji równą -0,40^,, która jest nazywana energią stabilizacji pola krystalicznego (CFSE crystal field stabilisation •rgy)

Dla jonu —►	konfiguracją podstawową jes J^1 ==>
| energia stabilizacji CFSE =-0,8^. zgodnie z poniższy równaniem:
*»f ł -»	=-0.8A«,	CFSE= -(2x0,4)^ =-0,8^ /, «
^e8	> =-UA«,	CFSE=-(3x0,4)^,= -!.^ -
1 ł +

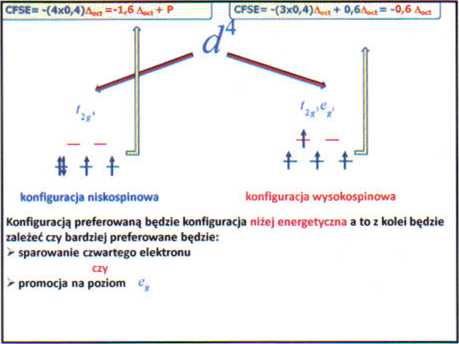
energii parowania P, - energia wymagana do transformacji dwóch e o spinach równoległych z dwóch różnych (zdegenerowanych) orbitali w spinowo sparowane e na tym samym orbitalu Dwa składniki mają swoją kontrybucję w odniesieniu do energii parowania P

r Obniżenie energii wymiany, który zachodzi podczas parowania się e Siły odpychania kulombowskiego pomiędzy spinowo sparowanymi e

Energia wymiany

o Wypełnione lub w połowie wypełnione powłoki ^ posiadają „specjalną stabilność", o Takie określenia bardzo często są zwodnicze.

o Bardziej powinniśmy rozważać energię wymiany pomiędzy danymi konfiguracjami, o To można wytłumaczyć na drodze zaawansowanej kwantowo-mechanicznej. o Idea problemu stosunkowo prosta :

Rozważmy dwa e na różnych orbitalach - odpychanie większe pomiędzy dwoma e jeśli posiadają spinu anty-równoległe aniżeli w sytuacji gdy ich spiny są równolegle jak np. w konfiguracji p' :    _p, -j.    4. 4

Różnica energii nazywa się energią wymiany K, tzn. jest dodatkową energią stabilizacji w odniesieniu do konfiguracji po lewej stronie. Całkowita energia wymiany wyrażona w terminach K (rzeczywista wartość K jest uzależniona od rodzaju atomu czy jonu):

Energia wymiany = spinami.

gdzie N jest ilością elektronów z równoległymi

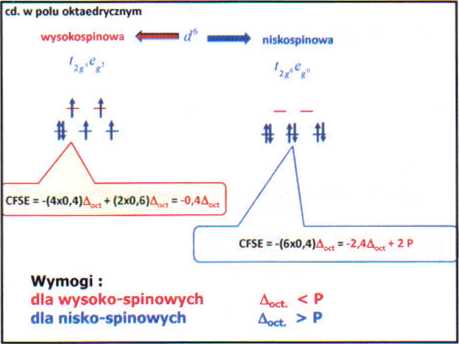
wartości CFSE dla wszystkich konfiguracji d^n w polu krystalicznym.
	Wysoko spihowe	- słabe pole	Nisko spinowe	silne pole
d^n	konfiguracja	CFSE	konfiguracja	CFSE
	elektronowa		elektronowa
d‘		•0.4A*,
(P	'..V	-o.sa*,
(P	':,V
d*	‘n<	■0.6A*.		-1,66* ♦ P
d^s		0	>u<	2.0 A*, + 2P
<r	'*V	■0.4^.		2,46,*, ♦ 2P
d^7		0.8A*.	‘u<	■w**p
<P	c«.’	-1.2A*.
<P	>u\'	■o,6A*.
dw		0

4