Ch koordynacyjna I (2)

2009-01-12

r rozważając różne teorie wiązań w kompleksach będziemy chcieli na ich podstawie tłumaczyć eksperymentalne fakty (właściwości magnetyczne, widma elektronowe) r skoncentrujemy się na kompleksach metali -d pierwszego szeregu r będziemy pamiętali, że wiązanie w kompleksach metali bloku -d nie jest fundamentalnie różne od tego w innych kompleksach A STĄD

^ będziemy chcieli wykazać możliwość zastosowania teorii VB, modelu elektrostatycznego jak i teorii MO do ich opisu.

różnica w podejściu do kompleksów metali bloku -d :

Punktem kluczowym jest to, że trzy z pięciu orbitali -d dla danej głównej liczby kwantowej ma swoje płaty skierowane pomiędzy osiami x, y i z podczas gdy pozostałe dwa orbitale są skierowane dokładnie wzdłuż tych osi jak jest to przedstawione na poniższym rysunku.

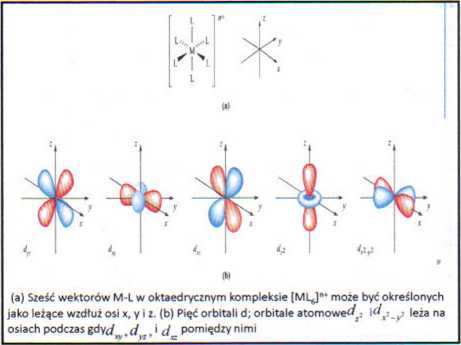
Konsekwencją tej różnicy jest to, że orbitale d w obecności liganda ulegają rozdzieleniu na grupy o różnej energii a typ rozdziału jak i wielkość różnicy energii zależy od rozmieszęzenią j natury Ugandą.

Zarówno właściwości magnetyczne jak i widma elektronowe uzależnione są od tego rozczepienia orbitali -d.

Stany wysoko i nisko spinowe

Jak już zdążyliśmy zauważyć, paramagnetyzm (patrz O^ ale i ponodtlenKi KOjp także ozon ki z paramagnetycznym jonemlOJ ) jest cechą charakterystyczną dla niektórych związków w układzie okresowym a więc i dla metali bloku -d.

Zgódźmy się, że dane magnetyczne pozwalają nam na określenie ilości niesparowanych elektronów. W wyizolowanym pierwszym bloku jonów metali -d 3d orbitale są zdegenerowane i elektrony zajmuje je zgodnie z reguła Hunda tak jak jest to przykładowo przedstawione na poniższym diagramie:

■I + + ++ ttł-ft--

Należy jednak pamiętać, że dla kompleksów oktaedrycznycłW badania magnetyczne wskazują, że powyższe kompleksy mogą zaliczać się do dwóch kategorii tzn.: paramagnetyków lub dlamagnetyków. Pierwszy z wymienionych nazywane są kompleksami wysoko-spinowymł i odnoszą się do tych w których pomimo że orbitale -d uległy rozczepieniu to w dalszym ciągu mamy cztery niesparowane elektrony. W diamagnetycznych kompleksachc/^nazywanych nisko-splnowymi odnosi się to do sytuacji gdzie elektrony zajmują parami trzy orbitale pozostawiając dwa orbitale puste.

Teoria Wiązań Walencyjnych

□    VB tworzenie się kompleksu obejmuje reakcję pomiędzy zasadą Lewis'a (Ugand) a kwasem lewis'a (metal lub jon metalu) z wytworzeniem koordynacyjnego wiązania kowalentnego (lub semipolarnego) między nimi.

□    Ten model wykorzystuje orbitale walencyjne metalu s, p I d dla tłumaczenia obserwowanych struktur i magnetycznych właściwości kompleksu.

□    Chociaż teoria VB w formie przedstawionej przez Paulinga w 1930 r. nie jest już stosowana w dyskusji kompleksów metali bloku d, to terminologia i wiele idei zostało zachowanych i pewna wiedza tej teorii w naszych dyskusjach wydaje się pozostawać niezbędna.

□    Poprzednio już opisywaliśmy zastosowanie hybrydyzacji ^SP ^SP ^ I ^SP‘^ w cząsteczkach o strukturze trygonalnej bi-piramidy, piramidy kwadratowej, oktaedru czy cząsteczki płasko kwadratowej.

□    Te same hybrydyzacje mogą być użyte w opisie wiązania w kompleksach metali bloku -d

Klasyczne użycie teorii wiązań walencyjnych w chemii koordynacyjnej zostab wprowadzone przez Paulinga w jego książce: The Naturę of the Chemical Bond’ J* ed. Come/I University; Ithaca, NY, 1960._

Ucz ba koordyn		Rozłożenie •tomów	Orbitale hybryduMce		Za pis	Przykład
2		Unio we	CLJ		W	[AgłNH.hr
3		Płaskie trójkątne	ffl		sp^2	[Hgł,t
4 4		Tetraedryczne Płaskie kwadratowe	H HS		sp^ł sp^2d	lFa8rJ> INHCN)«P
s s		Bipiramida t rygo na Ina Piramida kwadratowa	fi G9		sp^yd sp^y d	(CuCIJ*- (MICNM*
6 6		Oktaedr Graniastosłup trygonalny	ja		sp'd^2 sd’	(Co(NH,W prMeJ*-
7 7		Bipiramida pentagonalna Jedno wierzchołkowy trygonalny graniastosłup	52		sp'd' sp'd^2	(vłcN)Tr [NbF,J'
8 8 8		Kubki ny Owunastościan Kwadratowy antypryzmat	S-y	%	^sP^>d’f . ,, sp’d‘ ^SP^d	[PaF.P (Mo(CN),r [TaFJ>
9		Graniastosłup trygonalny t rój wie r zchołko wy			sp’d^i	P»eH,P

3