Blok d (6)

2009-01-12

Model Keperta tłumaczy kształt kompleksów metali bloku d [MLJ, czy [ML J"¹ poprzez rozważenie odpychania pomiędzy grupami L. Wolne pary elektronowe sq ignorowane. Dla liczby koordynacyjnej pomiędzy 2 a 6 następujgce rozłożenie atomów donorowych jest brane po uwagę:

2    liniowe

3    płaskie trygonalne

4    tetragonalne

5    trygonalne Bi-piramidatne lub piramida kwadratowa

6    oktaedryczne

Nie wszystkie przedstawione w tabeli rozłożenia dla danej liczby koordynacyjnej pomiędzy 2-9 są możliwe do przewidzenia na podstawi* modelu Keperta.

Przykładowo po rozważeniu odpychania pomiędzy ligandami cyjanowymi w [Cu(CN)j]² przewidywana sfera koordynacyjna powinna być płasko trygonalna tak jest w rzeczywistości.

Inną opcją z tej tabeli (rzadziej spotykaną) jest dla tego związku układ trygonalne piramidy ale on nie minimalizuje odpychania pomiędzy ligandami.

Jedną z bardziej klasycznych struktur dla której model Keptera nie daje poprawnej odpowiedzi są te dla kompleksów płasko kwadratowych gdzie elektronowy efekt jest zazwyczaj czynnikiem kontrolującym.

Innym czynnik, który może prowadzić do załamania się modelu Keptera może tkwić w ograniczeniach natury liganda. Przykładowo,

□ dla czterech atomów donorowych azotu w porfirynowym Ugandzie są ograniczone		Przed omówieniem geometrii w ciele stałym kompleksów bloku -d
do płasko kwadratowego układu;		pamiętajmy, że : wzór cząsteczki może być mylący w określeniu liczby
		koordynacyjnej. Przykładowo, w Cdl2
□ trójnożne Ugandy tzn. takie jak przedstawiono poniżej posiadają ograniczoną		■ Część dwóch warstw sieci Cdl2, jony Cd^7< pokazane są ^ w kolorze jasno szarym a jony na
fleksyjność co oznacza, że atom donora nie są w pełni swobodne do adopcji pozycji		Ar ,^vy ^w Każdy jon Cd jest usytuowany oktaedryczne a ■y > cząsteczkowe czy pseudo halogeny (np. [ ]-) ^ Q mogą zawierać mostki M- -M czy istnieć jako oligomery jak np. polimeryczny a-PdCI2:
wynikających z praw Keperta
ph£ Trójnożny Ugand to taki który zawiera trzy ramiona każde z donorowym atomem. Ramiona
te rozchodzą się promieniście od atomu centralnego lub grupy, ten centralny punkt może		O c-L n.
sam w sobie być donorowym atomem. □ Ugandy makrocykliczne są mniej fleksyjne niż te o otwartych łańcuchach

Dalsze dwuznaczności pojawiają się wtedy gdy wiązanie liganda może być opisane na więcej aniżeli jeden sposób. Spotykamy się z tym stosunkowo często w chemii organometalicznej jak np. w przypadku cyklopentadienylowego liganda:

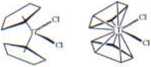
Jak widać z tego rysunku (brak zaznaczenia aromatyczności w pierścieniu) nie jesteśmy pewni czy ligand [r^-C^j zajmuje jedno czy pięć miejsc w sferze koordynacyjnej atomu metalu tak więc koordynacja centrum Ti(IV) w [(n^s-C5H_$)₂TiCIJ może być różna jak to przedstawiono na powyższych rysunkach.

1 UL    1

Przykłady kompleksów z liczbą koordynacyjną 2 należą do rzadkich i są w zasadzie ograniczone do: Cu(l), Ag(l), Au(l) i Hg(ll)

gdzie we wszystkich przypadkach konfiguracja jonu jest -d‘°.

Jako przykładowe możemy wymienić [CuCI₂]',    [Ag(NH_s)₂]*,

[Au(CN)₂], (RjP)AuCI, [AujRjP))' (gdzie R= alkil lub aryl) i Hg(CN)₂w których centrum metaliczne jest w liniowym otoczeniu.