DSCN1148 (2)

Ponieważ \BC\² || 0, więc 2|.dB|² < \AC\² + |BD|², MB|²^(MCf + |B0|²).

b) Jeśli podstawą dolną jest równoległobok ABCD, zaś gonią odpowiednio A_lB_lC,D,, to zpolecenia a) wynika, że \AB_t\² + |B_4,|² = 2(|/1/4,|² + \AB\\

MB,|² | |Bi4,|² | H\AA_t]² + \AD\²).

Dodając powyższe równości i uwzględniając warunek \AB\² + \AD\²    0,

mamy

4\AA_t|² < MB,|² + \BA_t\² + \ADi\² + |D/t,|², czyli

itóP^MBiP. + l^il² + \^>i\² + |ZM,|²).

5.56. Oznaczmy dodatkowo miary kątów dwuściennych o krawędziach AB, BCi AC odpowiednio S_t,S₂, S₃. Każdą ze ścian ABC, ACD i ABD rzutujemy na płaszczyznę ściany BCD (rys. 5.56).

A

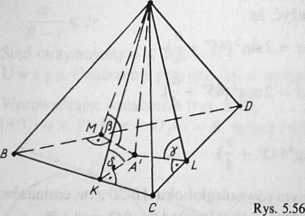
Wówczas mamy:

\A'l\ = |XI|cosy, \A'K\ = |AK|cosó₂, \A'M\ = \AM\ cos £ Stąd wynika, że

$tLA‘Bc ⁼ S₄ cosó_z, S^_A,_CD = S₂'COsy, S_Ł4BD = S₃cos/l.

W takim razie

S, = S₂cosy + S₃cos/ł + S₄cos<5₂.

W analogiczny sposób otrzymujemy następujące równości:

5₂    = S,cosy + S₃ cosa + S₄cos<5₃,

5₃    = S_t cosfi + S₂ cosa + S₄cos<5,,

5₄    = S, cos<5₂ + S₂cosó₃ + S₃cos<5,.

S,^2 = S,S2 cosy + SjSjCos/J + SjS4cosó2,	(1)
Sl = SjS2 cosy + S2S3 cosa + S2S4cosó3,	(2)
S3 = SlS3cosP + S2S3cosa + S3S4cosó,,	(3)
Sj = S,S4cosó2 + S2S4cos<53 + S3S4cosó,.	(4)

Równości (1), (2), (3) dodajemy stronami, zaś otrzymaną sumę odejmujemy stronami od równości (4), otrzymując tezę twierdzenia.

Obie strony każdej z otrzymanych równości mnożymy odpowiednio przez Sj. S₂, S₃, S₄ i otrzymujemy:

5.57. Stosując oznaczenia i metodę rozwiązania wykorzystane w zadaniu 5.56, mamy:

S, = S3 cos/3 + S4cosó2,	(1)
S2 = S3cosa + S4cosó3,	(2)
S3 = S, cos/? + S2cosa,	(3)
S4 = S, cos<52 + S2cosS3.	(4)

Każdą z obu stron otrzymanych równości mnożymy odpowiednio przez S,. S₂, S₃, S₄. Dodając stronami otrzymane w ten sposób równości: (1) i (2) oraz (3) i (4) otrzymamy tezę Sf + S\ = S| + SJ.

5.58. Załóżmy, że

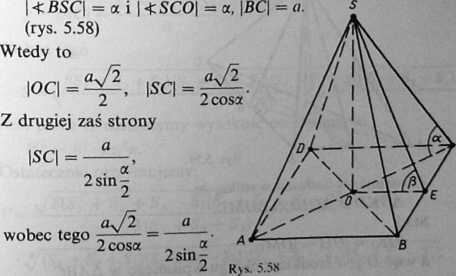
153