Hellwig i grafy (6)

M d CL OpfcK. j^du
‘ ’ u tu cocsvcK^y Y* 1flotloc£c) notiAAwęJlLSOtJC)
' t mo-K j' L, j-£ {J , -.. <m ^ m '
i. U
'Y
j,uX«_ ei^renkUjcA o>bj (*.SvucKjc)i*jX\
1, wiao<-'€vt ŁaV^jpoojq t ^o<J-o?c'gl' q AicŁot-ei^y £ (/asJx>Suc< m%, ,
>-* nc* X}£?W/jcjtAj S^.Sc'4
rej =0, cj^ l^jl^nr 5r,*j - nr.j , cjoty l/r.j I Y*
3 Ki«_ ęoddoMĆ hnaw-^^j (L ' k» CVUj w ij <^/0C^ •
pOlAlA-Jc/Cuj Łi<VU €w KMj vVU X., X, 'SWli'-^^ l^GU/f o^c' , <J ćLj /T,j
0O)/^^oUa^\ awu■£i^n/cjww> X., Vj /im? i'S^-Hi^|f (i/^cU/^oL1 , cjctcj - 'r,j „
Ó . [Ja c> cX Śt-CU/10 C^rod^A. c6& ot^ C^Ltj £? tfo j lW-dT< XV\A/t^HHg 1/t^bLc) cćo YlT^OtyC&ĆU-
e£cOi^9m elvij c> jaXto objVj'u*.coj q ce
Oo wjódjib^ i/tZwciedh<
jtrt^eo tniA^Mn a 2, UcŁrc^gfc? y O cXfrY c»~^<y •
" zwio^ynoa , /mC' /i (/) ^ Ctj Li^ouy^o^u m c/a^uj »h yacfQprcx^€
- vim e \'oo\aoa^'e i jctXoo hso^iące oJloiueMie jyoolcyyc^yj
- -t/K/Lenną , Ui-cLv^_ j*eLr 9>l^uXj diAW^Jboua^ <y •łjZ- oi-n^ćy/uj obj c*..rXt ć?tv?g , , Ł/^cx.c6tuA i jevł- ć> c^a/uj/w j?c'cXc^c\^' € lu Iba «.mx^nn^jcA c> Acojtsl jft kty ŁCc/Jsri € Ua'ct/c? j5cXu .
Ąójj^AgjŁ
?L3 7 -O>0* OKO
Ł =
'ł/ n
~0,M -0,2)6 X .
* 0,3^
j>0VUA£oUĄj Z-WU-^lOWAj/KA fOM^ędUsCj z^ms. £ viX/) -łw^ ?nmjvvu
X/f ^2 ' vf^ ć>J([ ^YOyJ^cli &0 t * ^2/f ,.
X/| X ^ fS-h'! v9>€ iss>bni'cje ( A>o ^a S “ ^
X Z X 'i w • e 1 'XkU£j e (^KCU>^>£<1 , ' ^32
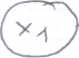

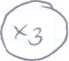
C^L* YAjodUtdl*' i- Lotrcjbeg O flootfcyrcK^yy j<Jyy>dU* j'eoimc<. ww f^wa. oLj ct j'nx cc^cj c« . ~ X a, j <xLoo \Vod*c<JOtsst c*^
- -ŁVVU. VI M Ct X >1 , potl^ce^ot 2 syoś^dd 'OY*y en^Uj,X<- o A (SI yźlr KJZ^ Lc^lLŚL-i ^
W^CŁ^Po^t -ŁVH . *■ H n Ct X 4 ,'e Jkf <łi' | n i -eł slua^&tooay,^ z£_ -Lw^e^ncj ob/ccs^o^*.
f^kl>Utl ■
ioicl. JO "ł"
b^a.3-// .- /(5
X4_
l^4/(
„ , ĆHH
X
Wyszukiwarka
Podobne podstrony:
Hellwig i grafy (0) frierocp HGjuiJiGia O- V i?nna, objaSouco^ne»-■ "L WU (X
Hellwig i grafy (10) ■ <r> łJ r> v tr -i « "X3T O CS ■i 1° *A. o " * -*1 * cjo
Hellwig i grafy (11) lad ALO n S ; C lriOM
Hellwig i grafy (13) ŁG (A ■ ^5 V 4 - Y a i - A - A Hm MŁX - 0,m A Ui* x* c *x :-A In Ł : 0,3 2 o,
Hellwig i grafy (14) Zad. 1 Przy budowie ekonometrycznego modelu popytu na pewne dobro (Y w tys. szt
Hellwig i grafy (15) Zad. 3 Budując model indywidualnej wydajności pracy robotników pewnej firmy (Y
Hellwig i grafy (16) 0,182 0,638 0,138 _ R 1 0 0,069 0
Hellwig i grafy (17) b) Podać ogólny wzór na liczbę kombinacji zmiennych objaśniających. Obliczenia
Hellwig i grafy (18) 9 3 0 2 10 2 2 1 10 4 0 1 Ob iczono wspó czynniki korelacji liniowej Pearso
Hellwig i grafy (19) t£$I* Zad. 9 Stosując metodę Hellwiga wybrać zmienne objaśniające do modelu eko
Hellwig i grafy (1) (-o - ‘ o,Ui l - -o,m 0, }60 - /i -O^Gi O, IW1 ■oM5 A o,n^
Hellwig i grafy (20) 1 -0,6 -0,8 0,3 -0,6 1 0,5 -0,2 -0,8 0,5 1 -0,7 0,3 -0,2 -0,7 1 Ro
Hellwig i grafy (21) Zad. 16 Podać przykład macierzy R, na podstawie której można zbudować następują
Hellwig i grafy (22) H, = 0,09; H2 = 0,49; H3 = 0,125; H4 = 0,36; K5 = {X1? X2}, K6 = {Xu X3}, K9 =
Hellwig i grafy (23) Metodą analizy grafów wybrać optymalną kombinację zmiennych objaśniających do m
Hellwig i grafy (24) Zad. 23 Mając dane zebrane w poniższej tabeli: Rok Wartość sprzedaży Cena (w
Hellwig i grafy (25) Cs
Hellwig i grafy (2) w J o: * V l V/j! K/i ; CU- -0U4- IoJlIiii _ ... . i-....._ 0,U£ i* = X; Vi a o
Hellwig i grafy (3) m * -ssiN :TTT7 7 ?n- OOTj vyi yov. yyy o 7rt> vso q ę. 0 hSO V 75%^ -
więcej podobnych podstron