z3

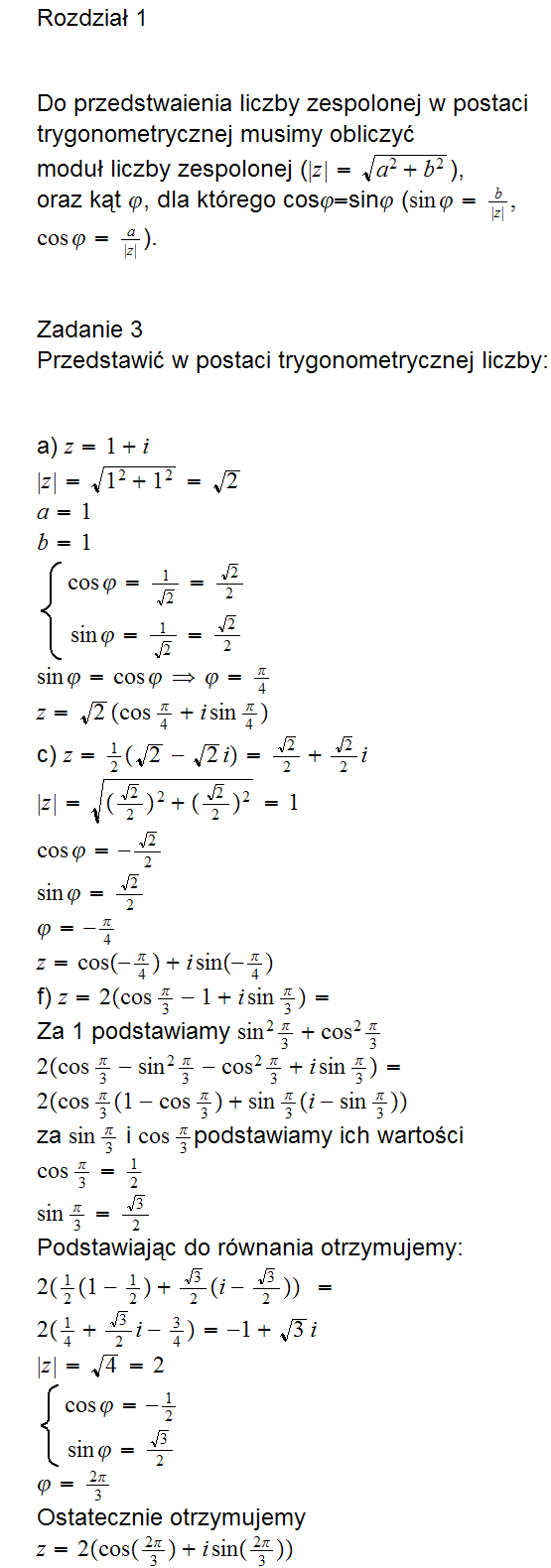
Rozdział 1

Do przedstwaienia liczby zespolonej w postaci trygonometrycznej musimy obliczyć moduł liczby zespolonej (|z| = Ja² + b²), oraz kąt ę, dla którego cos<p=sin<p (sin<p =

cos ę = ^).

Zadanie 3

Przedstawić w postaci trygonometrycznej liczby:

a) z = 1 + i |z| =    = ^2

a = 1 6 = 1

1 J2

COS (p = -^T = -V

Slll(p =

J2

1

A

2

J2

sin<p = cos ę =^> ę = y z = J2 (cos j + /sin j)

c)z= j(V2-V20-

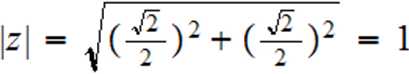
A

2

COS (p =

skup =

<P = “f

z = cos(-y) + ?sin(-y) f) z = 2(cos y - 1 + rsin y) =

Za 1 podstawiamy sin²-^ + cos²-|

2(cos y - sin²y - cos² y + rsin y) =

2(cos y (1 - cos y) + sin y (i - sin y)) za siny i cos f podstawiamy ich wartości

COSy = y

smf = ~

Podstawiając do równania otrzymujemy:

2(ł(!-ł)+#(>-#)) -

2(|f

|z| = V4 = 2

{COS(p = -y

sin<p =

(p = ²f-

Ostatecznie otrzymujemy

z = 2(cos(y^L) + rsin(^))