3582428841

1. CAŁKI NIEWŁAŚCIWE 1.1 CAŁKI NIEWŁAŚCIWE PIERWSZEGO RODZAJU

Def. 1.1.1 (całka niewłaściwa na półprostej)

Miech funkcja f    —>R bęcfcie całkowalna na przedziałach [a7] dla każdego T>a Całkę niewłaściwą pierwszego

rodzaju funkcji/ na pize dziale [a,®®) definiujemy wzorem:

J/(*)<*- =hm J/(y)dc .

oo

]/<»* jestzbiezna

ii

Jeżeli garnca po prawej stronie znaku równości jest skończona, to mówimy, ze całka niewłaściwa

Jeżeli garnca ta jest równa ®® lub -oo, to mówimy, ze całka jest i oz bieżna odpowiednio do oo lub -oo W pozostałych przypadkach mowuny, ze całka jest rozbieżna

Analogczme definiuje się całkę niewłaściwą pierwszego rodzaju na przedziale (-oo,6)

= lun J/(x)dc .

Def. 1.1.2 (całka niewłaściwa na prostej)

Miech funkcja / R —>R będzie całkowalna na przedziałach [ST] dla dowolnych Si T takich, ze -oo < S< T< oo Całkę niewłaściwą pierwszego rocfeąju funkcji f na przecbiale (-00,00) definiujemy wzorem

J/(v)rfc = //(x)dr +//(x)dc ,

gdzie a oznacza dowolną hczbę rzeczywistą Jeżeli obie całki po prawej stronie znaku równości są z bieżne, to mówimy, ze całka J* f(x)dx jest zbieżna. Jeżeli jedna z tych całek jest rozbieżna do -00 lub 00, a druga jest zbieżna albo rozbieżna

odpowiednio do -00 lub 00, to mówimy, ze całka jest rozbieżna do -00 lub 00. W pozostałych pizypadkach mówimy, ze całka ta jest rozbieżna

U*aga Jeżeli całki

Jf(x)dx, ff (x)dc

-00    <i

są zbiezne cfla pewnego ae R, to są zbiezne dla każdego ae R1 ich suma me

zalezy oda

Fakt 1.1J (zbieżność całek postaci

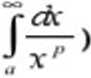
I-

Miecha>0 \Medy —

r J

r 1

Unaga Analogiczny fakt jest prawdziwy także dla całek I-, gdzie b<0. o ile funkcja podcałkowa jest poprawnie

określona

1.2 KRYTERIA ZBIEŻNOŚCI CAŁEK NIEWŁAŚCIWYCH PIERWSZEGO RODZAJU

Tw. 1.2.1 (kryterium porównawcze)

Jeżeli

10 ś J(x) < g(.\) dla każdego x e [a,oo),

2 funkcje/i g są całkowalne na pizedziałach [a 7] dla T>a,

oo

3. całka J"g(x)ćic jestzbiezna