1636661214

Jarosław Wróblewski

Analiza Matematyczna 1A, zima 2012/13

x-y

v^+ ^y+ ¥?

Zadania

Wyjaśnić, dlaczego poniżej są same BZDURY:

140.    Jim^^ = Jim^£ • ^lirn^ -/n — 0 • Jim^y/n — 0

141.    lim (\/n + l — y/n) = lim \/n+l— lim y/n = oo — oo = 0 1 dla n nieparzystych

dla n parzystych 143. lim k = k- lim I = fc-0 = 0

Zbadać zbieżność ciągu (a_n) określonego podanym wzorem; obliczyć granice ciągów zbieżnych, rozstrzygnąć czy ciągi rozbieżne mają granicę niewłaściwą

1

144. /~7    ¹⁴⁵' ²" n

149. ^⁺”²-⁶    ISo!⁵"⁵^²'⁶

3n⁴ + 7 1 + 2 + 4 + .. . + 2ⁿ

146. ^{4n2 + 3n} !47.i^±

72 + 1    n+2

1 — 2+3 —4 + 5 —6 + 151. -.    -

148.

5n³ + n² — 6

3n⁴ + 7 — 2 n

156.

1 + 3 + 9 + ... + 3” 1 + 2 + 3 + ... + n

3n⁴ + 7 153.

157.

154. n-(-l)ⁿ    155.

1 + \/n 3° + 3¹ +3² + 3³ + ...+3ⁿ

158.

(y/n+l + y/ń)⁷

7i³(l + 7vAT+2) v/3ⁿ + 2"

3ⁿ    y/& + l

160. yfń? 161. ^71 + 17    162. \/n² + 3n-n 163. n(Vn² + 7-n)

1

159. Vn

161. 7n + (^^)⁵V9^+I    _165> (-1)-

>/&

V3" + 2" + l

172.    ₁₇₃.

11t2³ + 7ti + 3 f (—l)ⁿ • 7z! dla n < 100

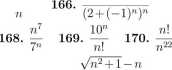
(\/72²+72+l — 72)² 1 1

V7T+7 —\/n

Ti² + 1 Tl² + 2 Tl² + 3    72² + 72    1

174. ——r -\—H—5—— + •■■ H—5- 175.

72³ + 1    72³ + 2    72³ + 3    72³ + 72

176. Obliczyć wartość granicy

+ o . «+••

n² 72² + 1    72² + 2

(72 + 1)²

₃n

lub uzasadnić, że granica nie istnieje. 177. Obliczyć granicę

°V9ⁿ+72²⁰¹⁰

„‘HSoS

72³ + k

'j“j 72⁴ + ( — 1)^ • k² '

Lista 3

- 20 -

Strony 18-41