4734120202
XIII Olimpiada Matematyczna Ouniorów ZAOAHIE 2 zawody drugiego atopiie ((3stycznia 2Ol0r.)
Dany jest trójkąt ostrokątny AfiC,» którym AC ^BC Punkt K jest spodkiem mpskoici tego trójkąta poprowadzone! z wuerzcbotkaC. Punkt O jest irodkiem okręgu opisanego na trójkącie A6C. Udowodnicie pola czworokątów AK0C. oraz BKOC &ą *own«. 1
~ założenie: A C< 6C
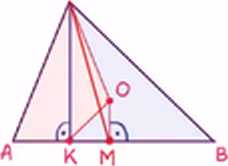
CKHOM =*. [CKO] =[CKM]
AKOC jest wypukły ^
[AK0Cj= [AKC] ł- [CKO] •
- fAKC] + [CKM] = [ACM] = ±(ABC]
[6K0C] » [ABC] - [AKOC] - ± [ABC] =»
=» [AKOC] - [BKOC]
Co byto do udowodnieni«*.
Wyszukiwarka
Podobne podstrony:
XIII Olimpiada Matematyczna 3uniorów Zadanie 3 zawody drugiego stopnia (Gstycznia ZOłBr.) Wyiracz ve
Zaomie i XIII Olimpiada Matematyczna Ouniorów zawody drugiego &topnia (G stycznia 2.0(8r.) istni
XIII Olimpiada Matematyczna Ouniorów ZADANIE Ą za*jody druc^eyo stopnie (fastycznia 2.018*.) Dany je
XIII Olimpiada Matematyczna Ounlorów ZKDhHlE 5 zawady drugiego stopnie (G stycznia 10 <6 r.) Kaid
Xfl OUmplaeLa Matematyczna J*/uotów ZADANIE Ą Zawody drugiego stopnia ( M stycznia 2017 r.) Czu «.ii
44 (190) Matematyka. Zbiór zadań do liceów i techników. Klasa IIIPołę trójkąta *6.63. Dany jest trój
X(l Olimpiada Matematyczna ^jn/dorów ZADANIE 5 Zarody drugiego otopnia ( Ą 3U)t2ftia 201? r.) Cfu is
Matematyczna GimnazjalistówVI Olimpiada Matematyczna Gimnazjalistów Zawody stopnia pierwszego 1
Matematyczna o www.omg.edu.plVII Olimpiada Matematyczna Gimnazjalistów Zawody stopnia pierwszego -
Obóz Naukowy Olimpiady Matematycznej Zwardoń, 29 maja - 12 czerwca 2008 (wydanie pierwsze)
Obóz Naukowy Olimpiady Matematycznej Zwardoń, 29 maja - 12 czerwca 2008 Dom wczasowy „Zgoda”, Zwardo
Wstęp Obóz Naukowy Olimpiady Matematycznej odbył się w dniach 29 maja -12 czerwca 2008 r. w Zwardoni
TnFundacja.pl Olimpiada ^ Matematyczna Juniorów . j
Top 73 bmp znane są tylko wyniki udziału w międzynarodowej olimpiadzie matematycznej uczniów szkół ś
XII Olimpiada Matematyczna Juniorów a-ET ♦ bFINAŁ Zadanie 1 b-f? *C Ctone ca dodatnie liczby całkowi
FINAŁ XII Olimpiada Matematyczna Juniorów Zadanie 2 Punkt D leżu na boku AB trójkąta ABC. Pdnkt E le
Finał Xll Olimpiada Matematyczna Juniorów Zadanie 3 Dane&atakie dodatnie liczby catkowite
Matematyczna 6€ www.omj.edu.plKwadratGazetka Olimpiady Matematycznej JuniorówNr 23wrzesień
więcej podobnych podstron