5987093068

DSFRiU matematyka finansowa, do użytku wewnętrznego Wydział Zarządzania UW    11

Stopa zmienna w oprocentowaniu składanym

Załóżmy, że dla kolejnych lat j = 1,2,n dane są efektywne (albo roczne) stopy procentowe: i⁽¹\ i®, ..., *("). Zatem w roku j-tym roczny czynnik oprocentowujący ma postać (1 + i^), a wartość kapitału w kolejnych latach wynosi

Si =    +

S, = A„(l + i^m)(l+i^ra),

Si = K₀(l + i^<1))(l + *¹¹⁾)(l + *^(a)),

Sn = A'o»+*^(1,)(l + i^m)(l+*^(s,)-..,(l + i^<"^>)-

Stąd łatwo wyprowadzić model oprocentowania rocznego przy stopie zmiennej w czasie:

Sn = A'o(l + i⁽¹>)(l + i^,2>)(l + •<*>).... (1 + i<">) = A'„ n < 1 + <°>), In = K„ ^ n (1 + »«>) - 1

Stopa przeciętna daje takie same odsetki w tym samym czasie, zatem spełnia równość

A„(i+ir=A„n(i+i«>)

3=1

czyli    _

1+?= jjnu+i®)

a więc czynnik oprocentowujący jest średnią geometryczną czynników oprocentowujących w poszczególnych latach, a wzór na stopę przeciętną ma postać:

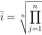
+ iW>) - 1.

Zadanie 28. Czy wartość kapitału 8,5 tys. zł kapitalizowana na koniec każdego roku gdy dzisiejsze oprocentowanie 2,5% będzie rosło w skali 0,25 punktu procentowego rocznie, ale nie więcej niż do 3,5% przekroczy po pięciu latach 10 tys.?

(nie, oprocentowanie w kolejnych latach 2,75%, 3%, 3,25%, 3,5%, 3,5% i warttość kapitału « 9949,67]    □

Zadanie 29. O ile musi wzrosnąć w trzecim roku oprocentowanie czteroletniej lokaty aby osiągnąć co najmniej 5900 zł jeżeli przez pierwsze dwa lata kapitał 5000 wygenerował 366,48 zł odsetek?

[pierwsze dwa lata 3,6%, a więc kolejne dwa lata trzeba 4,9% (co daje 5905,28) czyli wzrost o 1,3 punktu procentowego, albo przez stopę równoważną]    □

Zadanie 30. Bank BAA proponuje lokaty trzyletnie progresywną: w pierwszym roku oprocentowanie 5% i co rok wzrasta o 1 punkt procentowy, i stabilną: stale 6%. Którą wybrać?

[stopa równoważna progresywnej: 5,997%, a więc są równoważne - różnica przy kapitale 10 tys. 1 zl i 6 groszy]    □

Zadanie 31. Są trzy banki BAA, BAB, BAC, które przyjmują pieniądze tylko na 1 rok i oferują oprocentowanie, odpowiednio 3,5%, 4%, 3% rocznie. W jakiej kolejności lokować pieniądze w tych bankach by uzyskać jak najwięcej?

[nie ma znaczenia - stopa przeciętna zależy od iloczynu czynników oprocentowujących, a mnożenie jest przemienne] D