5987093085

DSFRiU matematyka finansowa, do użytku wewnętrznego Wydział Zarządzania UW    9

3. Oprocentowanie składane

Zasada oprocentowania składanego

Odsetki kapitalizuje się na koniec każdego okresu kapitalizacji.

Stąd wynika model oprocentowania składanego. W obliczaniu oprocentowania mamy 4 wielkości: K₀ - kapitał początkowy, i - stopa procentowa (i od ang. interest; zwykle podawana w procentach i ■ 100% ale wykorzystywana jako ułamek), n - liczba okresów kapitalizacji i S_n - kapitał po n okresach kapitalizacji przy procencie składanym. W tym przypadku n musi być liczba całkowitą dodatnią. Model oprocentowania składanego ma postać:

S_n = *o(l + *)"» In — Ko ((1 + *)" ^— 1) •

Z tych wzorów można obliczyć wszystkie wielkości:

Ko

S_n

(1+0*

ln

Si_l

Ko

ln(l + i) ’

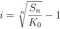
Zadanie 21. Kwotę 8 tys. zdeponowano w banku na 9% rocznie z rocznym okresem kapitalizacji. Jaka jest wartość depozytu po 6 latach, ile odsetek ten kapitał wygenerował? A gdy kwota 20 tys, 8%, 10 lat, a kwota 25 tys., 6,6% 15 lat.    □

Zadanie 22. Po ilu latach oprocentowania przy rocznej stopie 4,5% wartość kapitału 8000 przekroczy 10 tys. zł? [6 lat]    □

Zadanie 23. Jeżeli 500000 ma zamienić się w 700000 w ciągu 5 lat na jaki procent trzeba ulokować te kwotę zakładając kapitalizację kwartalną? (podać stopę nominalną)    □

Zadanie 24. Jaką kwotę trzeba ulokować w banku na 8% aby za 12 lat mieć 200 000?[79422,75]    □

Przykład. Po jakim czasie kapitał podwaja swoją wartość w oprocentowaniu składanym? Podstawiamy do wzoru

ln^

_n =_^K»

ln(l + i)

ln2

ln(l + i)

Na podstawie tego wzoru można ułożyć tabelę zależności czasu podwojenia kapitału od stopy oprocentowania:

stopa i	liczba lat do podwojenia	70/*	stopa i	liczba lat do podwojenia	70/i
1	69,66	70.00	50	1,71	1,40
10	7,27	7,00	60	1,47	1,17
20	3,80	3.50	70	1.31	1,00
30	2,64	2,33	80	1,18	0,88
40	2,06	1,75	90	1,08	0,78

Reguła 70

W oprocentowaniu składanym ze stopą i kapitał podwaja się po około — latach. _i_

□