123181

Twierdzenie 3

Z: (X, K,+, •) - przestrzeń wektorowa f: X->X - endomorfizm dimX=n

B=(^,ej,...,e_n)- baza A=M_f(B,B)

T: XeK jest wartością własną endomorfizmu <=> det(A - XI)=0 Def. 3

Z: An._n=[ajj] - macierz

X - nazywamy wartością własną macierzy A det(A - XI)=0.

Jeśli X jest wartością własną macierzy A to każdy wektor x: (A-2I)-x = Ó nazywamy wektorem własnym macierzy A dopowiadającym wartości własnej X macierzy A.

Wniosek:

1.    A=M_f (B, B) Np. f: Kⁿ->Kⁿ

X - jest wartością własną macierzy A jest wartością własną endomorfizmu f.

2.    x - jest wektorem własnym odpowiadającym wartości własnej X macierzy A <=> jest wektorem własnym odpowiadającym wartości własnej X endomorfizmu.

Uwaga

Ze względu na ścisły związek między X endomorfizmu, a X macierzy wszystkie twierdzenia udowodnione dla endomorfizmu są prawdziwe dla macierzy.

Def. 4	a..	a,„'		"1 0 0 1	0" 0		a1,-X a„
det(A-XI)=det(	_a„.	a,.,.	-X	0 0	1 0 ^0l.	) = det	21 . ^3 nl

- ±k⁺P_B.iV^v,+Pn.₂Xⁿ'^l+...+p,X+Po = A(A)

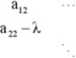
A(A) - nazywamy wielomianem charakterystycznym macierzy A (endomorfizmu).

Wartości własne macierzy (endomorfizmu) są pierwiastkami jego wielomianu charakterystycznego.

Uwaga

Wartości własne endomorfizmu nie zależą od wyboru bazy przestrzeni (są niezmiennikami endomorfizmu).

Wykład dr Magdaleny Sękowskiej strona 2 z 6 Część 12 -Wartości i wektory własne