TESTY NIEPARAMETRYCZNE

Test normalności Shapiro-Wilka

, gdzie
jest dystrybuantą rozkładu normalnego

próba prosta n-elementowa, pobrana z populacji o ciągłej dystrybuancie

poziom istotności

Postać statystyki testowej

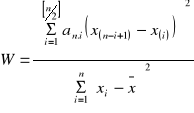
tablicowane współczynniki

uporządkowana próba według wartości rosnących

odczytujemy z tablic wartości krytycznych dla testu Shapiro-Wilka

Obszar odrzucenia
- zatem hipotezę H₀ odrzucamy gdy
-lewostronny obszar odrzucenia.

Test zgodności

, gdzie
jest zbiorem rozkładów o określonym typie postaci funkcyjnej dystrybuanty

n- elementowa próba (n>100, dane przedstawione są w postaci szeregu rozdzielczego o r przedziałach klasowych o liczebnościach
(i=1,…,r)

poziom istotności

Postać statystyki testowej

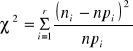
Statystyka ta przy założeniu prawdziwości
ma rozkład
o
stopniach swobody.

k - liczba szacowanych parametrów, które należy wstępnie wyznaczyć na podstawie próby

r - liczba przedziałów klasowych

- prawdopodobieństwo, że zmienna X przyjmuje wartość należącą do i-tego przedziału klasowego, gdy rozkład jest zgodny z

- liczba jednostek, które powinny się znaleźć w i-tym przedziale, przy założeniu, że zmienna ma rozkład zgodny z hipotetycznym

Obszar odrzucenia
(prawostronny), Wartość
odczytujemy z tablic dla (r-k-1) stopni swobody i danego

Test serii losowości próby (test medianowy)

próba jest losowa

próba n-elementowa

poziom istotności

Wyznaczamy Me z próby (w tym celu porządkujemy próbę niemalejąco).

Każdemu wynikowi z próby (według kolejności losowania elementów) przypisujemy symbol:

a gdy
,

b gdy
,

odrzucamy.

Zliczamy:

k - liczba serii

n₁- liczba symboli a

n₂ - liczba symboli b

Obszar odrzucenia dwustronny odczytujemy z tablic rozkładu liczby serii

,

Tablice
;

Test serii dla sprawdzenia hipotezy, że dwie próby pochodzą z jednej populacji

dane:

dwie próby o liczebnościach:

poziom istotności

Wyniki obu prób ustawiamy w jeden niemalejący ciąg. Elementy I próby oznaczamy symbolem a, próby II symbolem b. Zliczamy liczbę serii k

Obszar odrzucenia
odczytujemy z tablic

rozkładu liczby serii dla danych
tak, aby
(lewostronny obszar odrzucenia hipotezy zerowej).

Test niezależności chi-kwadrat

W teście niezależności chi-kwadrat hipotezy zerowa i alternatywana mają postać

H₀: cechy X i Y są niezależne (
)

H₁: cechy X i Y są zależne

sPostać statystyki testowej testu niezależności chi-kwadrat

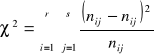
gdzie
są prawdopodobieństwami teoretycznymi.

Statystyka ta ma przy założeniu prawdziwości hipotezy H₀ asymptotyczny rozkład
z (r-1)(s-1) stopniami swobody.

Test ma prawostronny obszar odrzucenia, tzn. że na poziomie istotności α hipotezę H₀ odrzucamy na korzyść hipotezy alternatywnej, gdy
. W przeciwnym przypadku: na poziomie istotności α brak jest podstaw do odrzucenia H₀.

1

---