61896

Jak powstają równania Reynoldsa..

Stopień złożoności zmiennych stanu (min. Prędkości u) w ruchu burzliwym jest zbyt duży. by można było opisać go matematycznie, dlatego wykorzystuje się lokalnie uśrednione zmienne stanu, definiowane następująca relacją:

t+T

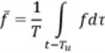
Obliczoną w ten sposób wartość średnią należy przyporządkować obliczeniowemu punktowi czasu t i otrzymujemy ciągły przebieg lokalnie uśrednionej fiinkcji:

Inny sposób znaleziema średnich wartości: wyznaczenie ich z uśrednionych równań ruchu. Aby otrzymać te równania trzeba przedstawić poszczególne zmienne w postaci sumy w-artości średnich oraz części fluktuacyjnej (oznaczonej symbolem ..prim"). np.: u — u + u' p = p + p'

Następnie sumy podstawiamy w odpowiedrue miejsca równań ruchu płynu i wykonujemy działania matematyczne. Otrzymujemy:

•    równanie ciągłości: dwu = 0

•    równanie dynamiczne: p^ = pf - gradp + pAii + div(-pu 0 u^f)

Wnioski:

•    równanie ciągłości dla prędkości lokalme uśrednionej u jest takie same jak równanie dla prędkości rzeczywistej

•    równanie dynamiczne dla zmieiuiych lokalme uśrednionych u i p jest prawie identyczne z równaniem dla znuermych rzeczywistych różni się członem:

(-pu'0uO

który zawiera uśredniony iloczyn diadyczny, utworzony z wektora prędkości fluktuacyjnej. Jest to tensor Reynoldsa (lub tensor naprężeń turbulentnych) oznaczany symbolem: fj