6830718837

4 Szeregi liczbowe

Niech {•%}^₌₁ biedzie dowolnym ciągiem liczbowym. Określamy ciąg {5,* }$£-•, na-s lęp u j ący m wzo re m

Sn — ;C | -f #2 + • • • + X_n — Xi

i=1

Definicja 4.1 (Szereg) Parę ciągów    _: {5«},T=i) nazgumnyszeregiem.

ciąg {S'„}*L_i ciągiem jego sum częściowych, a ciąg {x„}^_=iciągiem wyrazów tego szeregu.

Definicja 4.2 (Zbieżność i rozbieżność szeregu) Jeśli ciąg .sum częściowych szeregu jest zbieżny, to mówimy, że szereg jest zbieżny, albo mmowalny, a granicę ciągu sum częściowych nazywamy sumą szeregu.

Jeżeli ciąg ,mm częściowych nie. jest zbieżny, to ,szereg nazywamy rozbieżnym.

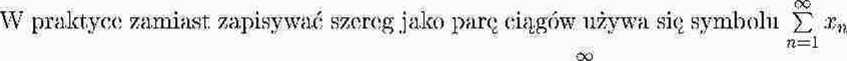
lub nawet Y.x_n . Tak samo oznacza sie sumę szeregu Y x_n zamiast lim S_n lub

«=i    " ^>:XJ

n

pełnego lim Y ^xi ■ Tern zapis nie jest konsekwentny. Istnieją, na przykład, szeregi

Oo

Y ^xn rozbieżne, a więc dla których nie istnieje suma Y x_n ■ Ze względu na tradycję

n=l    «=1

i wygodę używa się jednak tej formy.

Przykład 4.1 (Szereg geometryczny)

a £ 71, q € Tl, x_n =

n- a 5 = 1

S_n — o. 4- tz<j[i T o.cf' T ... T agⁿ

Dla q ^ l szereg geometryczny można więc zapisać tak

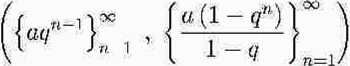
Jest. on zbieżny dla |ę| < 1 i wtedy S = lim S_n =    .

Przykład 4.2 Y =

n—1

Wyrazy x._n = tego szeregu możemy przekształcić następująco

1 111

ri^ź + n n(n + 1) n n + 1

Wtedy sumy częściowe

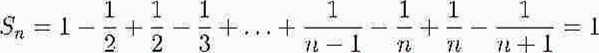
n +1

1

lim S_n = 1. a więc Y 7^7, = 1 •

n > 00    71=1 ⁷ u

11