4292417161

Całka krzywoliniowa skierowana

Całka krzywoliniowa zorientowana to wyrażenie:

J_l y)dx + Q(x, y)dy

L to krzywa po której całkujemy, a W(x, y) = (P(x, y), Q(x.y)) to wektor zaczepiony w punkcie (x,y), którego interpretacja fizyczna to siła. Natomiast interpretacja fizyczna samej całki to praca jaką wykonamy działając tą siłą wzdłuż krzywej L.

Podstawowy sposób liczenia całek krzywoliniowych zorientowanych jest podobny do niezorientowanych - wystarczy podstawić do wzoru. Wzór ten przy tradycyjnej parametryzacji to:

P(x,y)ix + Q(x,y)dy = £ [/’(*(«),»(t)) • x'(t) + Q(x(t).!/(*))■!/'(*)]<#

natomiast jeśli krzywa dana jest zależnością y = g(x), to mamy:

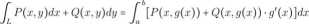
Przykład:

Policzmy całkę f_L ydx + x²dy dla krzywej danej parametrycznie x = 2t, y = t² - 1 gdzie t e [0,2], Mamy

x'{t) = 2 i y'{t) = 21, tak więc:

f_L ydx + x²dy = /„²[(t² - 1) • 2 + 4t² • 2t]dt = ... = pp

W niektórych szczególnych wypadkach możemy poradzić sobie inaczej (jeśli powyższa metoda prowadzi do skomplikowanych rachunków).

Jeśli istnieje funkcja F(x, y) taka, że F_x = P,F_y = Q. to tę funkcję nazywamy potencjałem, a P(x, y)dx+ Q(x, y)dy to jak wiadomo różniczka zupełna funkcji F. Jeśli obszar D w jakim się znajdujemy jest "porządny” (ściśle: jednospójny), a P,Q, P_y, Q'_x są ciągłe, to P(x, y)dx + Q(x, y)dy jest różniczką zupełną wtedy i tylko wtedy gdy P'_y = Q'_x. Co więcej, wówczas całka J_L P(x, y)dx + Q(x, y)dy nie zależy od drogi całkowania, a jedynie od punktu początkowego A i końcowego B, i mamy wtedy:

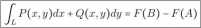
Przykład:

Policzmy całkę f_L(x + y)dx + (x - y)dy wzdłuż krzywej x = 3cost,y = 5sin£ i 0 < t < |. Mamy P(x,y) = x + y i Q(x,y) = x-y, a zatem P_y = 1 = Q'_x. Wiadomo zatem, że istnieje potencjał F. Skoro F_x = P(x,y), to:

F = f P(x, y)dx = f (x + y)dx = ^x² + yx + C(y)

Jeśli zróżniczkujemy tę równość po y, to pamiętając, że F_y = Q(x,y), dostajemy: x-y = x + C'{y)

skąd C'(y) = -y, czyli C(y) = -\y². Ostatecznie więc F(x,y) = ^x . Punkt początkowy (dla t = 0) to (3,0), a punkt końcowy (dla t = |) to (0,5). Końcowy wynik to zatem: f_L(x + y)dx + (x - y)dy = F(0,5) - F(3,0) = -17

13