7543473374

I

*

*

^A 197 t

* •

Quand on ajuste le modele (2) aux donnćes de la figurę A24, On

obtient les estimations

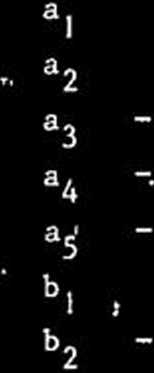
suivantes des coefficients

7,432

0,3915

1,755

3,427

6,833

0,9192    ¹³

0,01157

* .

<    JC

aoec un coefficient de corrćlation multiple de 0,99 et un F-observ4 de 70,88 a 6 et 9 degr4s de libertd, largement significatif au seuil de 0,0001%. On obtient ainsi un faisceau de courbes paralldles dont 1'allure est d4termin4e par bj et b2 J la figurę A24 montre oette allure (en trait gras) pour une valeur de la constante ćgale d la valeur moyenne des 5 constantes. On peut voir ąue l¹ on obtient ainsi une bien meilleure image de l'4volution moyenne des placettes qu'en ajustant une rśgression d l*ensemble des donndes sans distinction.

La mdme teahniąue peut 4viderment 4tre utilisde pour avoir des constantes et des pentes diffśrentes sur chaąue placette, ou encore une constante uniąue et des pentes diffćrentes. Cette demidre possibilitd peut s^Tav4rer trds utile avec les moddles ąui donnent des courbes asymptotiąues, corrne l ’ 4ąuation de SCHUMACHER.

Ainsi, avec une varżable expliqu4e Y et une seule variable expli-ccctive X, observ4es par exemple sur 3 placettes d plusieurs reprises, on peut.ajuster les moddles suiuants :

Pen te_u.ni^ue)__i_conste s_d if fer ente s :

Y    » a_} + a₂?₂ + a₃P₃ + bjX Pentes__e C__coristantes__derentes :

Y    = aj + a₂P₂ + a₃P₃ + bjX + b₂P₂X + b₃P₃X

tante_unięiue_^^ :

Y    * aj + bjX + ^b2^P2^{X + b}3^P3^X

Ou les et b^ sont les coefficients de regression a estimer, X et Y des

variables ąuelconąues et les Pj des variables ąui valent 1 pour la placette j et 0 pour les autres placettes.

r

-=--L ^ t    'J¹ W " -.^aT“J.^mmL'

t¹)    en anglais = common slope

(²)    en anglais = common intercept    *

%

• • ^