Lista zadań nr 4

Zad.1. Czas pracy pewnego rodzaju baterii ma rozkład normalny z odchyleniem standardowym równym 35
godzin. Dla 16 losowo wybranych baterii tego rodzaju otrzymano średni czas pracy 520 godzin. Czy na
poziomie istotności równym 0,05 można uznać, że przeciętny czas pracy tego rodzaju baterii jest większy
od 500 godzin?

Zad.2. Zeszłoroczne przychody ze sprzedaży w małych firmach pewnej branży w Polsce można uznać za
cechę o rozkładzie normalnym. Dla 25 losowo wybranych małych firm tej branży w Polsce otrzymano
średnie zeszłoroczne przychody ze sprzedaży równe 6,4 mln zł i odchylenie standardowe tych przychodów
wynoszące 1,3 mln zł. Przyjmując poziom istotności równy 0.05, należy sprawdzić, czy można uznać, że
przeciętne przychody ze sprzedaży wśród małych firm danej branży w Polsce w ubiegłym roku były
mniejsze od 7 mln zł.

Zad.3. Długość wśród śrub pochodzących z pewnej masowej produkcji ma rozkład normalny. Wyniki
pomiarów długości (w cm) pięciu losowo wybranych śrub z danej produkcji masowej są następujące: 8.31,
8.40, 8.35, 8.36, 8.28. Czy poziomie istotności 0,05 można uznać, że:

a) przeciętna długość śrub pochodzących z danej produkcji masowej różni się od 8,3 cm?
b) odchylenie standardowe długości śrub pochodzących z danej produkcji masowej jest większe od

0,01 cm?

Zad.4. Wiadomo, że rozkład wagi elementów wytwarzanych w pewnym zakładzie produkcyjnym jest
normalny z średnią wagą równą 90 g. Wyniki pomiarów wagi (w gramach) 9 losowo wybranych elementów
wytworzonych w tym zakładzie przedstawiały się następująco: 91.3, 88, 89.8, 91, 92, 90.5, 89.2, 87.6, 93.
Czy na poziomie istotności wynoszącym 0.02 można uznać, że odchylenie standardowe elementów
produkowanych w danym zakładzie jest większe od 1.5 g?

Zad.5. Badano miesięczne wydatki na prasę wśród czteroosobowych gospodarstw domowych w pewnym
dużym mieście. Dla 121 wylosowanych czteroosobowych gospodarstw domowych z danego miasta
otrzymano średnie miesięczne wydatki na prasę wynoszące 40zł i odchylenie standardowe tych wydatków
równe 11zł. Czy na poziomie istotności 0,01 można przyjąć, że przeciętne miesięczne wydatki na prasę
wśród rodzin czteroosobowych w danym mieście różnią się istotnie od 38 zł?

Zad.6. Czy na poziomie istotności równym 0.05 można przyjąć, że mniej niż 20% firm w pewnym powiecie
wykazało w ostatnim roku kalendarzowym stratę, jeżeli w wylosowanej próbie 110 firm stratę wykazało 14
firm?

Zad.7. Poniżej podany jest rozkład wartości nagród wśród losowo wybranych pracowników z pewnego
wielkiego zakład pracy:

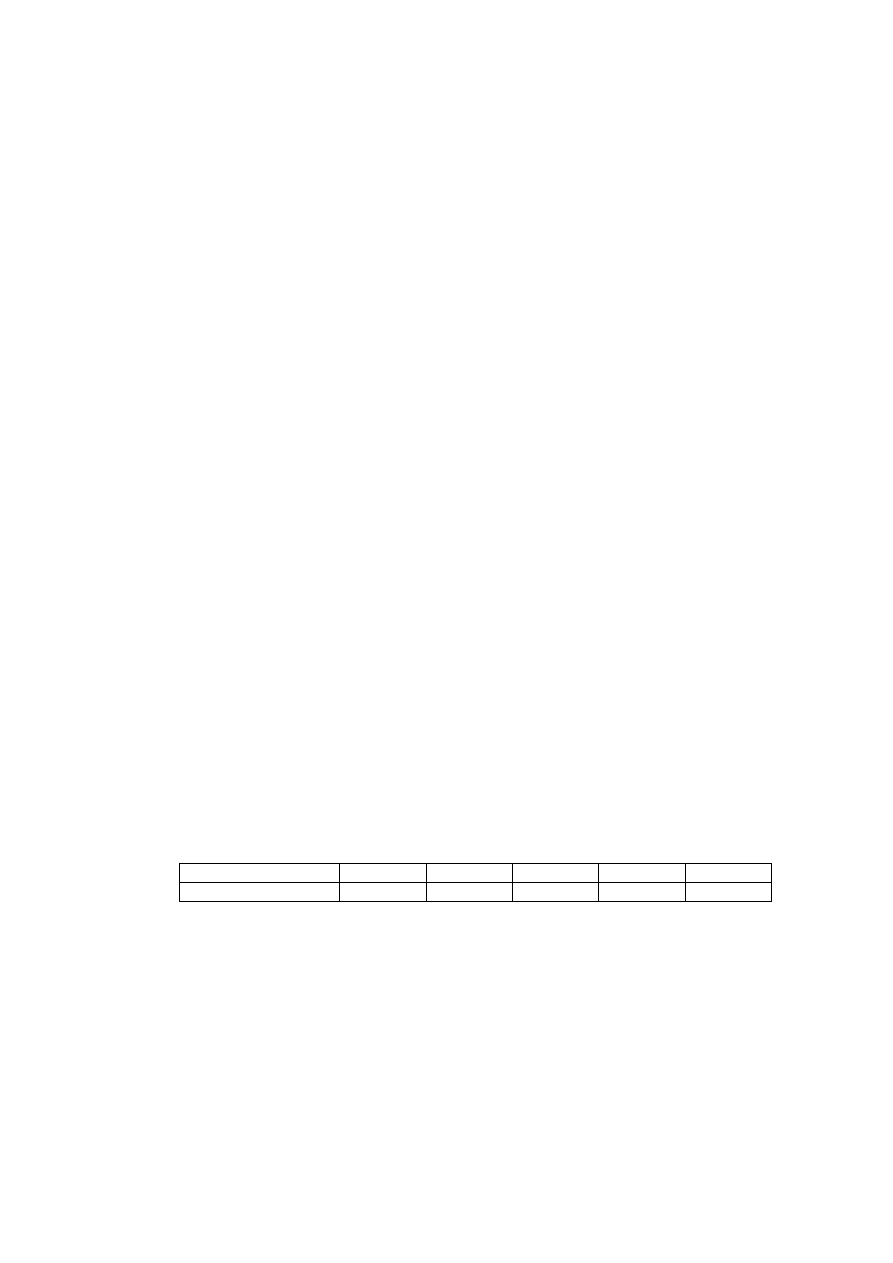
Wartość nagrody w zł

[200 – 240) [240 – 280) [280 – 320) [320 – 360) [360 – 400)

Liczba pracowników

20

30

25

15

10

a) Czy na poziomie istotności  = 0.05 można przyjąć, że przeciętna wartość nagrody pracownika z

danego zakładu przemysłowego jest mniejsza niż 300 zł?

b) Na poziomie istotności  = 0.1 zweryfikować sąd, że w 70% przypadków wartość nagrody

pracownika z danego zakładu pracy jest mniejsza od 320 zł.

Zad.8. Poddano badaniu 60-elementową próbę pobraną z populacji studentów ze względu na dwie cechy:
wzrost i przyrost obwodu klatki piersiowej przy wdechu. Współczynnik korelacji między badanymi
cechami wyniósł r=0,2819. Wiadomo, że badane cechy mają dwuwymiarowy rozkład normalny wśród
populacji studentów. Na poziomie istotności 0,01 zweryfikować hipotezę, że badane cechy są liniowo
niezależne.

Zad.9. Przyjęto, że stopy zwrotu z inwestycji A i B są niezależnymi zmiennymi losowymi o rozkładzie
normalnym z tą samą wariancją. Poprzednie stopy zwrotu były równe (w %):
A: 10, 15, 0, 1, 12, 7, 7, 8, 11, 12, 11, 14, 11, 8, 3, -2, 2,
B: 20, -10, 5, 9, -3, -12, -5, 1, 1, 6, 5, 16.
Czy na poziomie istotności równym 0.05 można przyjąć, że średnia stopa zwrotu inwestycji B jest większa
od średniej stopy zwrotu z inwestycji A?

Zad.10. Rozważano wiek pracowników w dwóch wielkich zakładach przemysłowych. Wyniki
eksperymentu na podstawie losowo wybranych grup pracowników z obu zakładów zestawiono w tabeli w
postaci szeregów rozdzielczych:

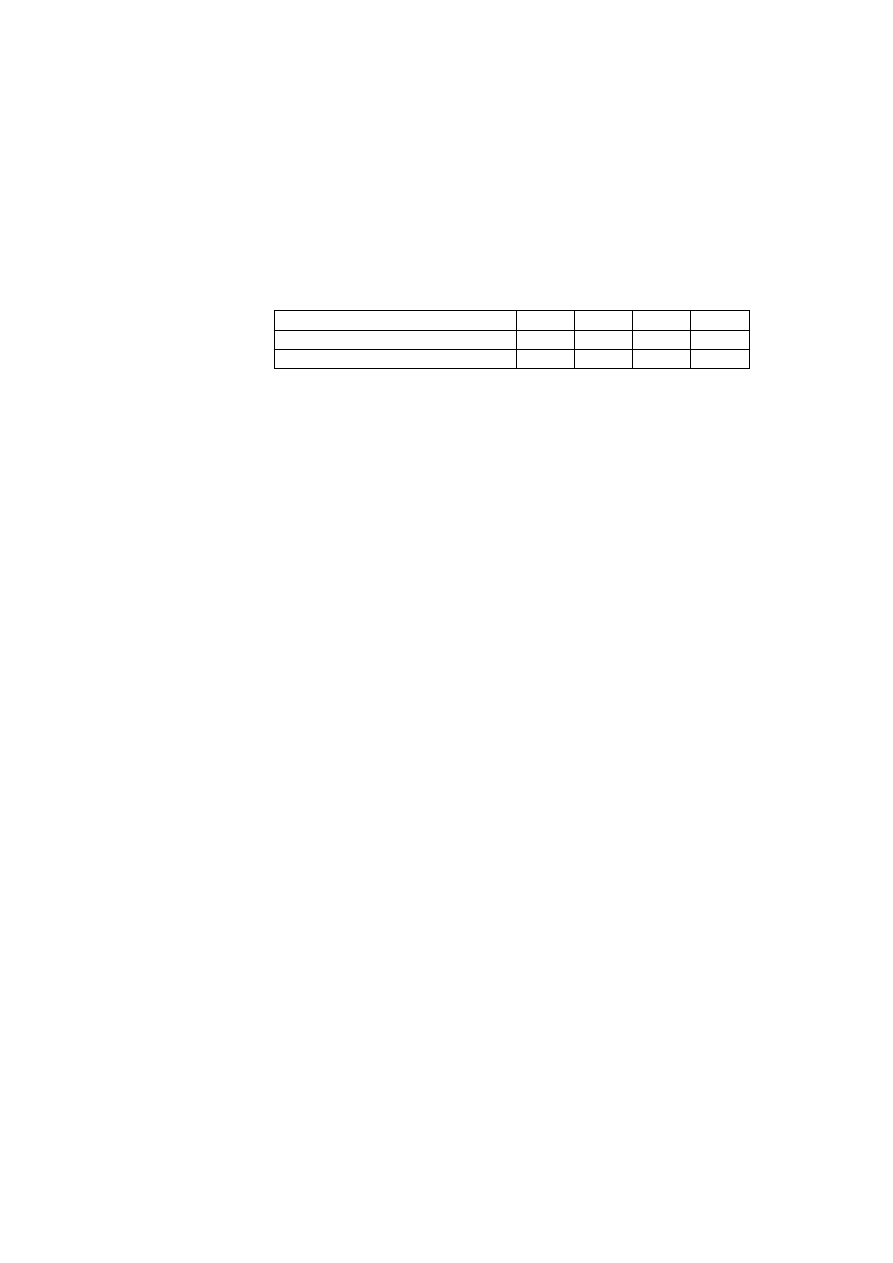
Wiek pracownika (w latach)

[20-30) [30-40) [40-50) [50-60)

Liczba pracowników w zakładzie A

15

25

30

30

Liczba pracowników w zakładzie B

10

30

45

15

a) Czy istnieją podstawy do odrzucenia hipotezy, że odsetek pracowników w zakładach A i B w wieku do

30 lat nie różni się istotnie? Przyjąć

0,05.

 

b) Czy można uważać, że średni wiek pracowników w zakładzie A jest większy niż w zakładzie B? Przyjąć

0,05.

 