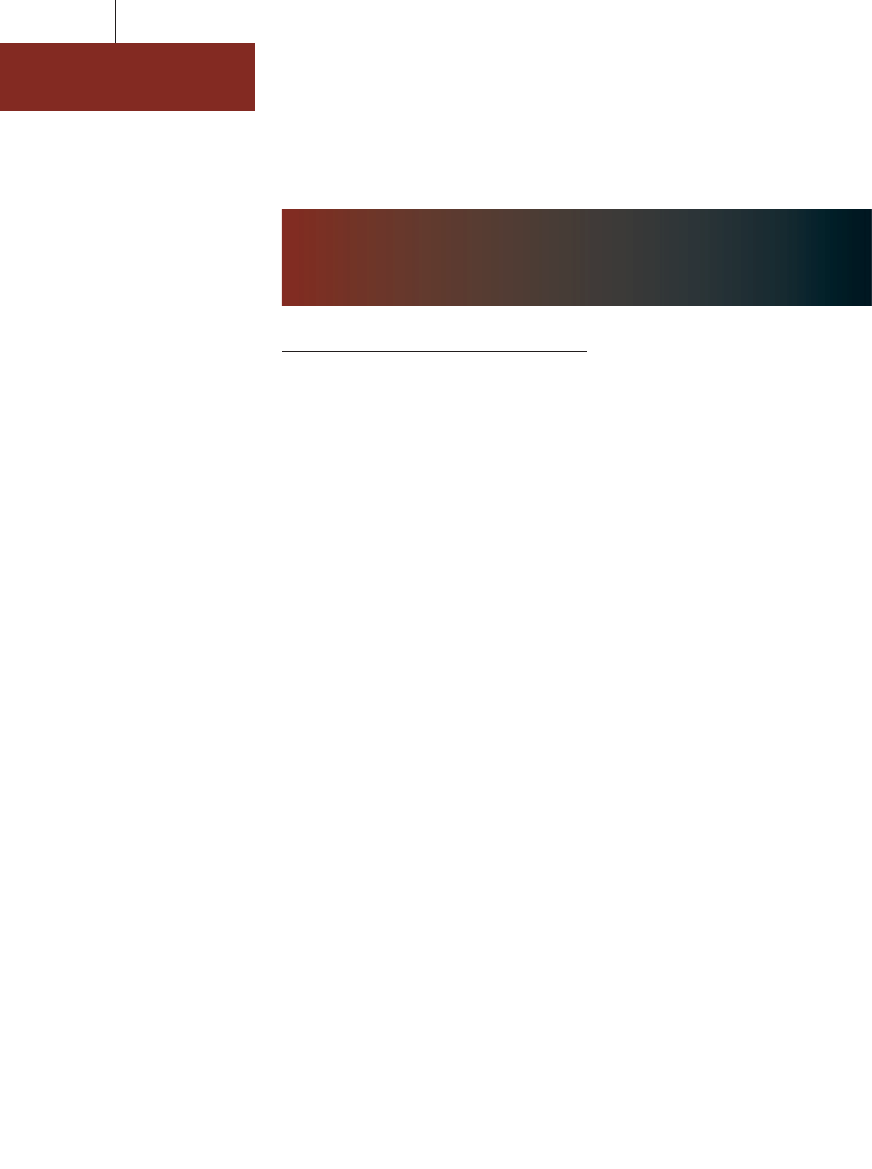
ZDJ¢CIE

DA

VID EMMITE

K

osmolodzy i fizycy czàstek elementarnych majà nie la-
da k∏opot. Choç najnowsze obserwacje potwierdzi∏y
standardowy model kosmologiczny, to jednak jest w nim

wcià˝ powa˝na luka – nie wiadomo, dlaczego WszechÊwiat
rozszerza si´ coraz szybciej. Gdy wyrzucimy w gór´ kamieƒ,
grawitacja ziemska sprawia, ˝e nie ucieka on z naszej plane-
ty, lecz stopniowo wytraca pr´dkoÊç i spada z powrotem. Po-
dobnie odleg∏e galaktyki rozbiegajàce si´ po Wielkim Wybu-
chu powinny zwalniaç w wyniku wzajemnego przyciàgania
grawitacyjnego. Tymczasem ich ucieczka ulega przyÊpiesze-
niu. Naukowcy najcz´Êciej przypisujà to przyÊpieszenie dzia-
∏aniu tajemniczego czynnika zwanego ciemnà energià, lecz
ich pi´kne wywody w niewielkim stopniu oparte sà na fizycz-
nych konkretach. Nie ulega jedynie wàtpliwoÊci, ˝e w naj-
wi´kszej obserwowanej skali grawitacja zachowuje si´ doÊç
nieoczekiwanie, dzia∏ajàc odpychajàco, a nie przyciàgajàco.

Z praw fizyki wynika, ˝e êród∏em grawitacji jest materia

i energia, a zatem za dziwnà grawitacj´ powinna odpowiadaç
jakaÊ dziwna odmiana materii lub energii. W ten sposób do-
chodzi si´ do poj´cia ciemnej energii. Ale mo˝e nale˝a∏oby
zmieniç same prawa. Taki precedens w fizyce ju˝ by∏ – prawo
powszechnego cià˝enia sformu∏owane przez Newtona
w XVII wieku zosta∏o w 1915 roku zastàpione przez ogólnà
teori´ wzgl´dnoÊci Einsteina, poniewa˝ okaza∏o si´ nie doÊç
uniwersalne. Zakres stosowania ogólnej teorii wzgl´dnoÊci
równie˝ jest ograniczony; w szczególnoÊci napotyka ona trud-
noÊci na skrajnie ma∏ych odleg∏oÊciach – w skali opisywanej
przez mechanik´ kwantowà. I podobnie jak ogólna teoria
wzgl´dnoÊci zastàpi∏a fizyk´ newtonowskà, ona sama pr´dzej
czy póêniej ustàpi miejsca kwantowej teorii grawitacji.

Przez te lata fizycy zaproponowali kilka koncepcji grawita-

cji kwantowej, z których najbardziej znana jest teoria strun.
Gdy grawitacja dzia∏a w mikroskali – na przyk∏ad w centrum
czarnej dziury, gdzie olbrzymia masa zajmuje obszar o sub-

atomowych rozmiarach – zaczynajà odgrywaç rol´ egzotycz-
ne kwantowe w∏asnoÊci materii. Teoria strun opisuje w∏aÊnie,
jak wyglàda wówczas prawo grawitacji.

Badacze zajmujàcy si´ teorià strun powszechnie przyjmu-

jà, ˝e na du˝ych odleg∏oÊciach efekty kwantowe nie odgry-
wajà ˝adnej roli. Jednak odkrycia dokonane w kosmologii
w ciàgu ostatnich kilku lat sk∏aniajà ich do zrewidowania te-
go poglàdu. Cztery lata temu wraz z moimi wspó∏pracowni-
kami zada∏em pytanie, czy teoria strun nie zmienia praw gra-
witacji nie tylko na najmniejszych, ale i na najwi´kszych
odleg∏oÊciach. Aspektem teorii strun, który móg∏by byç za to
odpowiedzialny, sà dodatkowe wymiary – dodatkowe kierun-
ki, w których mogà poruszaç si´ czàstki. Teoria strun prze-
widuje, ˝e przestrzeƒ, oprócz trzech zwyk∏ych, ma jeszcze
szeÊç lub siedem wymiarów.

Kwintesencja z nicoÊci

W PRZESZ

¸OÂCI

zwolennicy teorii strun argumentowali, ˝e owe

dodatkowe wymiary sà zbyt ma∏e, abyÊmy mogli je zaobser-
wowaç lub si´ w nich poruszaç. Jednak najnowsze badania wy-
kaza∏y, ˝e niektóre z tych nowych wymiarów, a nawet wszyst-
kie, mogà mieç w istocie wielkoÊç nieskoƒczonà. Nie widaç
ich nie dlatego, ˝e sà zbyt ma∏e, lecz dlatego, ˝e czàstki two-
rzàce nasze cia∏a sà faktycznie uwi´zione w trzech wymia-
rach. Jedynà czàstkà niepodlegajàcà tym ograniczeniom jest
grawiton, przenoszàcy oddzia∏ywania grawitacyjne, co w kon-
sekwencji powoduje zmian´ prawa grawitacji.

Gdy astronomowie zaobserwowali przyÊpieszenie kosmicz-

nej ekspansji, w pierwszym odruchu przypisali je dzia∏aniu
tzw. sta∏ej kosmologicznej. Ta s∏ynna sta∏a, wprowadzona
w swoim czasie przez Einsteina, który wycofa∏ si´ zresztà
póêniej z tego pomys∏u, reprezentuje energi´ samej przestrze-
ni. Ca∏kowicie pusta przestrzeƒ, pozbawiona wszelkiej ma-
terii, wcià˝ zawiera∏aby energi´ o g´stoÊci mniej wi´cej

48

ÂWIAT NAUKI MARZEC 2004

RAPORT SPECJALNY

Georgi Dvali

PrzyÊpieszenie kosmicznej ekspansji byç mo˝espowodowane jest
nieub∏aganà ucieczkà grawitacji z naszego Êwiata, a nie ciemnà energià

OCE

CIEMNOÂCI

M

GRAWITONY, wydostawszy si´ z naszego WszechÊwiata,
penetrujà wy˝sze wymiary przestrzeni. Ucieczka ta
uwidacznia si´ dopiero w bardzo du˝ej skali.

10

–26

kg/m

3

. Pomimo ˝e sta∏a kosmologiczna nie jest sprzecz-

na z ˝adnymi dotychczasowymi danymi obserwacyjnymi, wie-
lu fizykom trudno si´ do niej przekonaç. Problem tkwi w wy-
jaÊnieniu, dlaczego mia∏aby ona mieç tak niskà wartoÊç, ˝e nie
odgrywa∏a we WszechÊwiecie ˝adnej roli w ciàgu niemal ca-
∏ej jego historii, w tym równie˝ we wczesnych epokach, kie-
dy si´ kszta∏towa∏. Co gorsza, jest ona znacznie mniejsza ni˝
skala energetyczna procesów fizycznych, w wyniku których
mia∏a powstaç [patrz: Adam G. Riess i Michael S. Turner
„Od supernowych do antygrawitacji”, strona 42].

Aby ominàç ten problem, wielu fizyków zaproponowa∏o,

by uznaç, ˝e êród∏em przyÊpieszenia nie jest sama przestrzeƒ,
lecz pole energetyczne wype∏niajàce jà na podobieƒstwo roz-
rzedzonej mg∏y. Energia potencjalna pewnych przestrzennie
jednorodnych pól mo˝e powodowaç efekty przypominajàce
w znacznym stopniu efekty sta∏ej kosmologicznej. Powszech-
nie uwa˝a si´, ˝e jedno z tego rodzaju pól, znane jako pole
inflacyjne, odpowiada∏o za okres przyÊpieszonej ekspansji,
czyli inflacji, we wczesnym WszechÊwiecie. Niewykluczone,
˝e pojawi∏o si´ teraz inne takie pole, które sprawia, ˝e Wszech-
Êwiat wchodzi w kolejny okres inflacji. Pole to nazwano kwin-
tesencjà. Podobnie jak sta∏a kosmologiczna musi ono mieç
zadziwiajàco ma∏à wartoÊç, lecz jego zwolennicy utrzymujà,
˝e ∏atwiej zaakceptowaç wielkoÊç dynamicznà, która ustabi-
lizowa∏a si´ na niskim poziomie, ni˝ sta∏à przyrody majàcà
od razu znikomo ma∏à wartoÊç [patrz: Jeremiah P. Ostriker
i Paul J. Steinhardt „WszechÊwiat kwintesencyjny; Âwiat Na-
uki, marzec 2001].

Zarówno sta∏a kosmologiczna, jak i kwintesencja sà konkret-

nymi przypadkami tego samego ogólniejszego poj´cia ciem-
nej energii. Na razie brak przekonujàcych dowodów przema-
wiajàcych za któràkolwiek z nich, dlatego w∏aÊnie fizycy
powa˝nie rozwa˝ajà teorie z wieloma wymiarami. Zaletà do-
datkowych wymiarów jest to, ˝e samoistnie zmieni∏yby pra-
wa rzàdzàce grawitacjà. Zarówno w teorii Newtona, jak
i w ogólnej teorii wzgl´dnoÊci si∏a przyciàgania grawitacyj-
nego dwóch cia∏ maleje proporcjonalnie do kwadratu odle-
g∏oÊci mi´dzy nimi. Przyczyna tego le˝y w geometrii – zgod-
nie z zasadà sformu∏owanà przez XIX-wiecznego fizyka
Carla Friedricha Gaussa, si∏a oddzia∏ywania grawitacyjnego
jest wyznaczona przez g´stoÊç linii si∏ pola grawitacyjnego,
a w miar´ zwi´kszania odleg∏oÊci linie te rozk∏adajà si´ na co-
raz wi´kszym obszarze brzegowym. W trójwymiarowej prze-

strzeni obszar brzegowy jest dwuwymiarowà powierzchnià,
której pole wzrasta proporcjonalnie do kwadratu odleg∏oÊci.

W przypadku przestrzeni czterowymiarowej obszar brzego-

wy by∏by trójwymiarowà obj´toÊcià, czyli jego wielkoÊç wzra-
sta∏aby proporcjonalnie do szeÊcianu odleg∏oÊci, tym samym
g´stoÊç linii si∏ mala∏aby równie˝ proporcjonalnie do szeÊcia-
nu odleg∏oÊci. A zatem oddzia∏ywania grawitacyjne by∏yby
s∏absze ni˝ w Êwiecie trójwymiarowym. Ze wzgl´dów, które
omówi´ póêniej, w skali kosmologicznej to os∏abienie grawi-
tacji spowodowa∏oby przyÊpieszanie kosmicznej ekspansji.

Skoro grawitacja mo˝e przedostaç si´ do dodatkowych wymia-

rów przestrzennych, to dlaczego nie zauwa˝yliÊmy tego do tej po-
ry? Dlaczego standardowe prawo odwrotnych kwadratów w
trzech wymiarach tak doskonale opisuje ruch pi∏ek golfowych,
pocisków rakietowych i planet? Teoria strun zwykle odpowiada
na to, ˝e owe dodatkowe wymiary sà zwarte – zwini´te w ma-
leƒkie p´tle skoƒczonych rozmiarów. Przez d∏ugi czas przyjmo-
wano, ˝e wielkoÊç tych p´tli jest rz´du tzw. d∏ugoÊci Plancka,
czyli oko∏o 10

–35

m, lecz najnowsze badania teoretyczne i do-

Êwiadczalne wykazujà, ˝e mo˝e ona dochodziç nawet do 0.2 mm
[patrz: Nima Arkani-Hamed, Savas Dimopoulos i Georgi Dva-
li „Niewidoczne wymiary WszechÊwiata”; Âwiat Nauki, paê-
dziernik 2000]. Gdy wymiary sà zwarte, ich wp∏yw na grawita-
cj´ ogranicza si´ do niewielkich odleg∏oÊci – porównywalnych
z promieniem ich zwini´cia lub mniejszych. Na du˝ych odle-
g∏oÊciach obowiàzujà standardowe prawa grawitacji.

Wi´êniowie brany

KONCEPCJA ZWARTYCH WYMIARÓW

napotyka jednak trudnoÊci.

Mo˝na na przyk∏ad zapytaç, dlaczego cz´Êç wymiarów jest
ciasno zwini´ta (te dodatkowe), podczas gdy pozosta∏e (te,
które znamy) rozciàgajà si´ w nieskoƒczonoÊç. Ujmujàc
t´ kwesti´ inaczej – pod wp∏ywem materii i energii we Wszech-
Êwiecie zwarte wymiary, jeÊli coÊ ich nie stabilizuje, powinny
si´ rozwinàç. Jednà z interesujàcych mo˝liwoÊci jest fakt, ˝e
to pola podobne do magnetycznych, przewidywane przez teo-
ri´ strun, zapobiegajà zarówno kurczeniu si´, jak i ekspansji
wymiarów. Inne mo˝liwe rozwiàzanie pojawi∏o si´ w 1999
roku. Byç mo˝e wszystkie wymiary, tak˝e te dodatkowe, roz-
ciàgajà si´ w nieskoƒczonoÊç, natomiast WszechÊwiat jest
trójwymiarowà powierzchnià, czyli membranà (w skrócie
„branà”) w wielowymiarowym Êwiecie. Zwyk∏a materia uwi´-
ziona jest w obr´bie brany, lecz niektóre oddzia∏ywania, jak
grawitacja, potrafià si´ z niej uwolniç.

Grawitacja ma wi´c takie zdolnoÊci jak Houdini – i tym za-

sadniczo ró˝ni si´ od innych oddzia∏ywaƒ. Zgodnie z kwanto-
wà teorià pola oddzia∏ywania grawitacyjne sà przenoszone
przez czàstki zwane grawitonami. Przyciàganie grawitacyjne
to wynik przep∏ywu grawitonów mi´dzy dwoma cia∏ami, po-
dobnie jak oddzia∏ywania elektromagnetyczne wynikajà z prze-
p∏ywu fotonów pomi´dzy dwiema czàstkami na∏adowanymi.
W przypadku statycznego pola grawitacyjnego grawitony ma-
jà charakter „wirtualny” – mo˝na zmierzyç wywo∏ane przez
nie efekty, lecz nie da si´ ich zaobserwowaç jako samoistnych
czàstek. S∏oƒce utrzymuje Ziemi´ na orbicie, emitujàc wirtu-
alne grawitony, poch∏aniane przez naszà planet´. „Rzeczywi-
ste”, czyli mo˝liwe do bezpoÊredniego zaobserwowania, gra-
witony odpowiadajà falom grawitacyjnym, które sà emitowane
w pewnych warunkach [patrz: W. Wayt Gibbs „Zmarszczki w
czasoprzestrzeni”; Âwiat Nauki, czerwiec 2002].

50

ÂWIAT NAUKI MARZEC 2004

n

Astronomowie zazwyczaj przypisujà przyÊpieszanie ekspansji

WszechÊwiata tajemniczej ciemnej energii. Mo˝e ono jednak
tak˝e oznaczaç, ˝e konwencjonalne prawa fizyczne
w bardzo du˝ej skali przestajà obowiàzywaç.

n

Nowego prawa grawitacji dostarczyç mo˝e teoria strun, jedna

z najpowa˝niejszych prób stworzenia zunifikowanej teorii
ostatecznej. Teori´ strun na ogó∏ uwa˝a si´ za teori´ skal bardzo
ma∏ych; ma ona jednak tak˝e konsekwencje makroskopowe.

n

W szczególnoÊci teoria ta przewiduje, ˝e WszechÊwiat ma

dodatkowe wymiary, do których grawitacja, w przeciwieƒstwie
do zwyk∏ej materii, mo˝e si´ przedostaç. Ta ucieczka powoduje
trwa∏e zakrzywienie kontinuum czasoprzestrzennego
i przyÊpieszenie kosmologicznej ekspansji. Mo˝e mieç te˝
niewielki, lecz dajàcy si´ zaobserwowaç wp∏yw na ruch planet.

Przeglàd / Ucieczka grawitonów

Zgodnie z teorià strun grawitony, jak wszystkie inne czàst-

ki, faktycznie sà oscylacjami maleƒkich strun. Jednak w prze-
ciwieƒstwie do elektronów, protonów i fotonów, które stano-
wià oscylacje strun otwartych, analogicznych do strun
skrzypcowych, grawitony sà oscylacjami strun zamkni´tych
w p´tl´, podobnych do gumowej opaski. Joseph Polchinski
z Kavli Institute for Theoretical Physics w Santa Barbara po-
kaza∏, ˝e koƒce strun otwartych nie mogà „trzepotaç” w prze-
strzeni, lecz muszà „trzymaç si´” brany. GdybyÊmy spróbo-
wali oderwaç takà otwartà strun´ od brany, rozciàgnie si´
ona jak elastyczny sznurek, lecz jej koniec pozostanie w bra-
nie. W odró˝nieniu od strun otwartych struny zamkni´te nie
ulegajà zwiàzaniu z jakimkolwiek miejscem i mogà si´ swo-
bodnie przemieszczaç po ca∏ej 10-wymiarowej przestrzeni.

Tak naprawd´ grawitony nie majà jednak pe∏nej swobody.

Gdyby jà mia∏y, klasyczne prawo grawitacji przepad∏oby z kre-
tesem. Twórcy hipotezy nieskoƒczonych wymiarów, Lisa Ran-
dall z Harvard University i Raman Sundrum z Johns Hop-
kins University, zaproponowali, by przyjàç, ˝e swoboda
grawitonów jest ograniczona, poniewa˝ dodatkowe wymiary
w przeciwieƒstwie do tych dotàd znanych charakteryzujà si´
bardzo du˝à krzywiznà, tworzàc jak gdyby wàwóz o stromych
Êcianach, z którego trudno si´ wydostaç.

Sedno sprawy tkwi w tym, ˝e w konsekwencji silnego za-

krzywienia dodatkowe wymiary majà skoƒczonà obj´toÊç,
pomimo ˝e rozciàgajà si´ w nieskoƒczonoÊç. A w jaki sposób
nieskoƒczona przestrzeƒ mo˝e mieç skoƒczonà obj´toÊç?
Wyobraêmy sobie, ˝e wlewamy d˝in do znajdujàcego si´ w kie-

MARZEC 2004 ÂWIAT NAUKI

51

GRAFIKA BRY

AN CHRISTIE; èRÓD¸

O JEFFREY WEEKS (

czter

owymiar

owa kostka

)

OD FLATLANDII DO CZTERECH WYMIARÓW

HAS¸O ZE S¸YNNEGO PLAKATU Gerry’ego Mooneya brzmi: „Grawitacja
to nie tylko ciekawa idea, lecz prawo”. Jednak w rzeczywistoÊci prawo
to daje si´ w znacznym stopniu naginaç. Na przyk∏ad zale˝y ono
od liczby wymiarów przestrzennych. Niepodwa˝alnym faktem jest to,
˝e grawitacja s∏abnie wraz z odleg∏oÊcià, poniewa˝ w miar´ wzrostu
odleg∏oÊci rozk∏ada si´ na coraz wi´kszy obszar brzegowy (zaznaczony
na czerwono na rysunkach poni˝ej).

DWA WYMIARY. Brzeg jest jednowymiarowy
(linia) i jego wielkoÊç wzrasta proporcjonalnie
do odleg∏oÊci. A zatem si∏a oddzia∏ywania
grawitacyjnego maleje odwrotnie
proporcjonalnie do odleg∏oÊci.

Cz∏owiek o masie 100 kg
wa˝y∏by na powierzchni
Ziemi 10

45

N

Waga 10

3

N

y

x

x

y

z

z

x

w

y

Odleg∏oÊç

Si∏a grawitacji

Przestrzeƒ 2-wym.

Przestrzeƒ 3-wym.
Przestrzeƒ 4-wym.

Waga 10

–39

N

TRZY WYMIARY. Brzeg jest dwuwymiarowy,
tak wi´c si∏a oddzia∏ywania grawitacyjnego
maleje odwrotnie proporcjonalnie do kwadratu
odleg∏oÊci. Przedmioty w danej odleg∏oÊci
sà l˝ejsze, ni˝ by∏yby w dwóch wymiarach.

CZTERY WYMIARY. Przypadek
ten jest trudny do wizualizacji,
lecz zasadnicza idea jest taka
sama. Brzeg jest trójwymiarowà
obj´toÊcià, a zatem grawitacja
stosuje si´ do prawa odwrotnych
szeÊcianów. Przedmioty sà
jeszcze l˝ejsze ni˝
w przestrzeni trójwymiarowej.

liszku bez dna martini. Promieƒ tego kieliszka maleje od-
wrotnie proporcjonalnie do g∏´bokoÊci, do nape∏nienia go
wystarczy wi´c w takim przypadku skoƒczona iloÊç d˝inu.
Ze wzgl´du na krzywizn´ kieliszka wi´kszoÊç jego obj´toÊci
znajduje si´ u góry. Jest to sytuacja bardzo podobna do tej,
z jakà mamy do czynienia w modelu Randall–Sundruma. Ob-
j´toÊç dodatkowych wymiarów przestrzennych skupia si´ wo-
kó∏ brany, na której si´ znajdujemy, co sprawia, ˝e grawitony
przez wi´kszoÊç czasu muszà przebywaç w pobli˝u brany.
Prawdopodobieƒstwo wykrycia grawitonu szybko maleje
w miar´ oddalania si´ od brany. W ˝argonie fizyków kwanto-
wych oznacza to, ˝e funkcja falowa grawitonu ma maksimum
na branie – efekt ten nosi nazw´ lokalizacji grawitacji.

Pomimo ˝e model Randall–Sundruma to pod wzgl´dem

koncepcyjnym coÊ zupe∏nie innego ni˝ idea zwartych wymia-
rów, prowadzà one do bardzo podobnych wniosków. Obydwa
modyfikujà prawo grawitacji jedynie na krótkich odleg∏oÊciach,
a nie w du˝ej skali, ˝aden z nich nie nadaje si´ zatem do roz-
wiàzania problemu przyÊpieszania kosmicznej ekspansji.

Fizyka na branie

TRZECIA KONCEPCJA

jednak˝e przewiduje za∏amanie si´ stan-

dardowego prawa grawitacji w skali kosmologicznej i t∏uma-
czy kosmologiczne przyÊpieszenie bez odwo∏ywania si´
do ciemnej energii. W 2000 roku wraz z Gregorym Gabada-
dzem i Massimem Porratim, pracujàcymi obecnie w New

York University, postawiliÊmy tez´, ˝e dodatkowe wymiary
majà dok∏adnie taki sam charakter, jak trzy wymiary prze-
strzenne, z którymi mamy do czynienia na co dzieƒ – nie sà
ani zwarte, ani silnie zakrzywione.

Nawet w takim przypadku grawitony nie mogà si´ ca∏kiem

swobodnie poruszaç tam, gdzie chcà. Emitowane przez gwiaz-
dy i inne cia∏a znajdujàce si´ na branie, potrafià przedrzeç
si´ do dodatkowych wymiarów, ale dopiero po przebyciu pew-
nej krytycznej odleg∏oÊci. Grawitony zachowujà si´ mniej
wi´cej tak, jak dêwi´k w metalowej blasze. Gdy uderzymy
w blach´ m∏otkiem, powstaje fala dêwi´kowa, która prze-
mieszcza si´ po jej powierzchni. Jednak rozchodzenie si´
dêwi´ku nie jest w tym przypadku zjawiskiem ÊciÊle dwuwy-
miarowym – cz´Êç energii rozprasza si´ w otaczajàcym powie-
trzu. W pobli˝u miejsca uderzenia straty energii sà zaniedby-
walnie ma∏e, lecz w miar´ oddalania stajà si´ coraz wi´ksze.

Ubytki energetyczne tego rodzaju majà istotne znaczenie

dla oddzia∏ywania grawitacyjnego, jeÊli odleg∏oÊç pomi´dzy
cia∏ami jest wi´ksza od wartoÊci krytycznej. Wirtualne grawi-
tony wykorzystujà wszelkie dost´pne drogi pomi´dzy cia∏ami
i mo˝liwoÊç obejÊcia przez inne wymiary stwarza olbrzymià
liczb´ dodatkowych trajektorii, co istotnie zmienia efekty gra-
witacyjne. Rzeczywiste grawitony po wydostaniu si´ do inne-
go wymiaru ginà raz na zawsze i dla nas, wi´êniów brany, wy-
glàda to tak, jak gdyby rozp∏yn´∏y si´ w sinej dali. ObecnoÊç
dodatkowych wymiarów ujawnia si´ tak˝e w bardzo ma∏ych

52

ÂWIAT NAUKI MARZEC 2004

GRAFIKA BRY

AN CHRISTIE

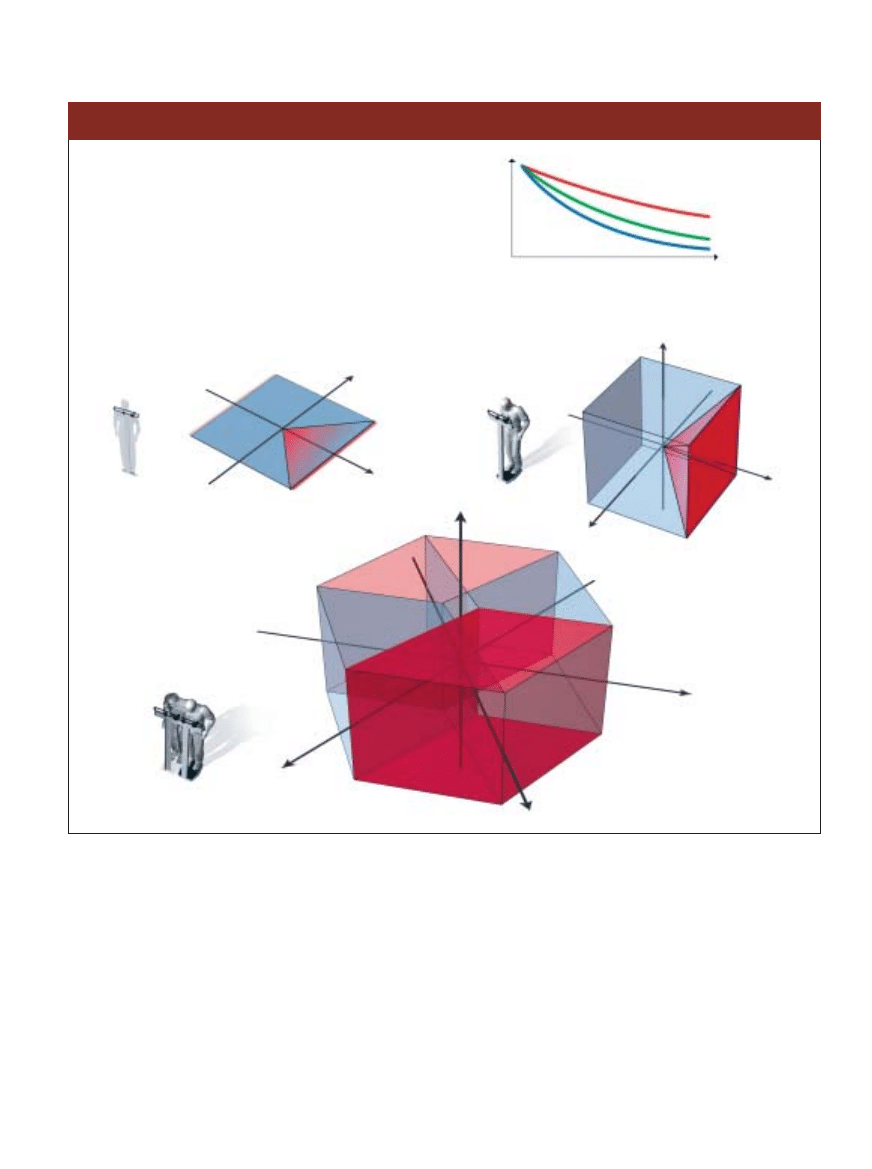
TRZY SPOSOBY WPROWADZENIA DODATKOWEGO WYMIARU

ALBERT EINSTEIN i inni uczeni jego czasów, zw∏aszcza Theodor Kaluza i Oskar Klein, byli wr´cz zakochani w idei ukrytych
wymiarów przestrzeni. Hipoteza ta od˝y∏a w teorii strun. Dla jasnoÊci przedstawmy sobie nasz trójwymiarowy WszechÊwiat
jako siatk´ na p∏aszczyênie. Przez ka˝dy z w´z∏ów tej siatki przechodzi linia, która reprezentuje jeden z dodatkowych wymiarów.

KONWENCJONALNA TEORIA STRUN. Zwolennicy
teorii strun d∏ugo przyjmowali, ˝e dodatkowe
wymiary majà skoƒczonà wielkoÊç – ma∏e p´tle
subatomowych rozmiarów. Poruszajàce si´
w takim wymiarze ˝yjàtko powróci∏oby
po jakimÊ czasie do punktu wyjÊcia.

MODEL NIESKO¡CZONEJ OBJ¢TOÂCI. Autor
i jego wspó∏pracownicy wysun´li tez´,
˝e dodatkowe wymiary sà nieskoƒczone
i niezakrzywione, zupe∏nie jak znane nam
trzy wymiary.

MODEL RANDALL–SUNDRUMA. Ostatnio
zwolennicy teorii strun doszli do wniosku,
˝e dodatkowe wymiary sà nieskoƒczone,
lecz na tyle silnie zakrzywione, ˝e prawie
ca∏a ich obj´toÊç jest skupiona wokó∏
naszego WszechÊwiata.

Zwarte
wymiary

Hiperboliczne
wymiary

Liniowe
wymiary

skalach, podobnie jak w przypadku wymiarów zwartych i mo-
delu Randall–Sundruma. Dla odleg∏oÊci poÊrednich – wi´k-
szych ni˝ rozmiary strun, lecz mniejszych ni˝ odleg∏oÊç uciecz-
ki – grawitony grzecznie siedzà sobie w trzech wymiarach,
pos∏uszne klasycznemu prawu grawitacji.

Kluczem do tego scenariusza jest sama brana, b´dàca obiek-

tem materialnym. Grawitacja rozchodzi si´ w niej w odmien-
ny sposób ni˝ w otaczajàcej przestrzeni ze wzgl´du na to, ˝e
zwyk∏e czàstki, jak elektrony i protony, mogà istnieç wy∏àcz-
nie w obr´bie brany. Nawet w na pozór pustej branie k∏´bi
si´ ca∏e mnóstwo wirtualnych elektronów, protonów i innych
czàstek, nieustannie powstajàcych i znikajàcych w wyniku
fluktuacji kwantowych. Czàstki te sà zarówno êród∏em grawi-
tacji, jak i same jej podlegajà, natomiast otaczajàca bran´
przestrzeƒ jest naprawd´ pusta. Przemykajàce przez nià gra-
witony mogà oddzia∏ywaç jedynie ze sobà.

Analogi´ mo˝e stanowiç tu materia∏ nieprzewodzàcy, jak

tworzywo sztuczne, ceramika lub czysta woda. Taki materia∏
w odró˝nieniu od pró˝ni zawiera elektrycznie na∏adowane
czàstki i podlega wp∏ywom pola elektrycznego. Czàstki na∏a-
dowane nie mogà p∏ynàç swobodnie przez dielektryk, jak
w przypadku materia∏ów przewodzàcych pràd, mogà jednak
zmieniaç swój rozk∏ad w jego obr´bie. Po przy∏o˝eniu pola
elektrycznego dielektryk staje si´ elektrycznie spolaryzowany.
Czàsteczki wody na przyk∏ad obracajà si´ tak, ˝e ich dodat-
nio na∏adowane koƒce (dwa atomy wodoru) skierowane sà
w jednà stron´, a ujemnie na∏adowane koƒce (atom tlenu)
w drugà. W czàsteczce chlorku sodu dodatnie jony sodu
i ujemne jony chloru lekko si´ rozsuwajà.

Zmieniony rozk∏ad ∏adunków generuje w∏asne pole elek-

tryczne, które cz´Êciowo neutralizuje pole przy∏o˝one z ze-
wnàtrz. Dielektryk mo˝e zatem wp∏ywaç na propagacj´ fotonów,
które w istocie sà po prostu oscylacjami pola elektromagne-
tycznego. Fotony przenikajàce do dielektryka polaryzujà go
i same z kolei ulegajà cz´Êciowo zneutralizowaniu. Aby do te-
go dosz∏o, d∏ugoÊç fali fotonu musi mieÊciç si´ w okreÊlonych
granicach: fotony o du˝ej d∏ugoÊci fali (niskoenergetyczne) sà
zbyt s∏abe, aby wywo∏aç polaryzacj´ dielektryka, natomiast fo-
tony o ma∏ej d∏ugoÊci fali (wysokoenergetyczne) oscylujà na-
zbyt szybko, aby czàstki na∏adowane zdà˝y∏y zareagowaç. Z te-
go wzgl´du woda jest przezroczysta dla fal radiowych (o du˝ej
d∏ugoÊci) i dla Êwiat∏a widzialnego (o ma∏ej d∏ugoÊci), a po-
ch∏ania mikrofale (o poÊredniej d∏ugoÊci). Zjawisko to sta∏o si´
podstawà dzia∏ania kuchenek mikrofalowych.

Podobnie fluktuacje kwantowe przekszta∏cajà bran´ w gra-

witacyjny odpowiednik dielektryka. To tak jak gdyby bran´
wype∏nia∏y czàstki wirtualne o dodatniej i ujemnej energii.
Po przy∏o˝eniu zewn´trznego pola grawitacyjnego brana zo-
staje grawitacyjnie spolaryzowana. Czàstki o energii dodatniej
odsuwajà si´ nieco od czàstek o energii ujemnej. Grawiton,
który odpowiada oscylacjom pola grawitacyjnego, mo˝e spo-
laryzowaç bran´ i zostaç unicestwiony, jeÊli jego d∏ugoÊç
fali zawiera si´ w odpowiednich granicach – czyli jak obli-
czyliÊmy, przypada w zakresie od 0.1 mm (lub mniej, w zale˝-
noÊci od liczby dodatkowych wymiarów) do mniej wi´cej
10 mld lat Êwietlnych.

Unicestwione zostajà jedynie grawitony wlatujàce do bra-

ny lub z niej wylatujàce. Grawitony, podobnie jak fotony, sà fa-
lami poprzecznymi, które oscylujà prostopadle do kierunku
propagacji. Grawiton wchodzàcy do brany lub wychodzàcy

z niej zwykle przemieszcza czàstki po branie – w jedynym
kierunku, w jakim mogà si´ poruszaç. A zatem grawitony ta-
kie sà w stanie spolaryzowaç bran´, przy czym same ulegajà
unicestwieniu. Natomiast grawitony poruszajàce si´ w obr´-
bie brany starajà si´ wypchnàç czàstki poza bran´, co nie jest
mo˝liwe, tak wi´c nie polaryzujà one brany i poruszajà si´,
nie napotykajàc ˝adnego oporu. W praktyce wi´kszoÊç grawi-
tonów zawiera si´ mi´dzy tymi dwiema skrajnoÊciami. Mknà
one przez przestrzeƒ pod kàtem do brany i mogà przebyç na-
wet miliardy lat Êwietlnych, zanim ulegnà unicestwieniu.

Efektowne krzywobranie

BRANA EFEKTYWNIE IZOLUJE SI

¢

w ten sposób od dodatkowych

wymiarów. JeÊli grawiton o poÊredniej d∏ugoÊci fali próbuje
si´ wydostaç lub przeniknàç do brany, czàstki w jej obr´bie
przemieszczajà si´ i udaremniajà to. Grawitony tym samym
zmuszone zostajà do poruszania si´ wzd∏u˝ brany, a zatem
oddzia∏ywania grawitacyjne spe∏niajà prawo odwrotnych
kwadratów. Jednak grawitony o du˝ej d∏ugoÊci fali potrafià
swobodnie przemierzaç dodatkowe wymiary. Nie odgrywa-
jà one wi´kszej roli na ma∏ych odleg∏oÊciach, zaczynajà nato-
miast dominowaç w skali rz´du w∏asnej d∏ugoÊci fali. Prawo
grawitacji staje si´ wówczas coraz bli˝sze prawu odwrotnych
szeÊcianów (jeÊli tylko jeden z wymiarów jest nieskoƒczony),

MARZEC 2004 ÂWIAT NAUKI

53

GEORGI DVALI dorasta∏ w Gruzji, gdy by∏a ona jednà z republik
Zwiàzku Radzieckiego. Doktorat uzyska∏ w Instytucie Fizyki im.
E. Andronikaszwilego w Tbilisi. Pracowa∏ na Uniwersytecie w
Pizie, w CERN, Europejskim Laboratorium Fizyki Czàstek pod Ge-
newà, i w Mi´dzynarodowym Centrum Fizyki Teoretycznej w TrieÊcie,
nast´pnie zosta∏ wyk∏adowcà New York University. Lubi zmagaç si´
z grawitacjà podczas jazdy na rowerze górskim, jak równie˝ wyko-
rzystywaç t´ tajemniczà si∏´ do szusowania po zboczach.

O

AUTORZE

PONURE WI¢ZIENIE BRANOWE

PRZYKRO POWIEDZIEå, ale nawet jeÊli dodatkowe wymiary
istniejà, ludzie nigdy nie b´dà mogli ich penetrowaç. Czàstki,
z jakich zbudowane sà nasze cia∏a – elektrony, protony,
neutrony – odpowiadajà oscylacjom strun otwartych
i ze swojej natury zwiàzane sà na sta∏e z branà, która
stanowi nasz WszechÊwiat. Grawitony, czàstki przenoszàce
oddzia∏ywania grawitacyjne, wymykajà si´ tym wi´zom,
poniewa˝ nie majà koƒców.

Brana

Grawiton

Elektron

prawu odwrotnoÊci czwartych pot´g (jeÊli dwa wymiary sà
nieskoƒczone), a nawet jeszcze bardziej strome. Ka˝dy z tych
przypadków oznacza os∏abienie grawitacji.

Wraz z Cédrikiem Deffayetem (obecnie w Institut d’Astro-

physique de Paris) i Gabadadzem stwierdziliÊmy, ˝e dodatko-
we wymiary nie tylko os∏abiajà oddzia∏ywania grawitacyjne,
lecz tak˝e wymuszajà przyÊpieszenie kosmologicznej ekspansji
bez koniecznoÊci postulowania istnienia ciemnej energii. Ma
si´ ochot´ powiedzieç, ˝e z powodu os∏abienia grawitacyjnych
wi´zów, które hamujà ekspansj´, ucieczka grawitonów zmniej-
sza opóênienie do tego stopnia, i˝ staje si´ ono ujemne, czyli
przechodzi w przyÊpieszenie. Mamy tu jednak do czynienia ze
znacznie bardziej subtelnym zjawiskiem – nale˝y si´ przyjrzeç,
w jaki sposób ucieczka ta zmienia ogólnà teori´ wzgl´dnoÊci.

Zasadniczà ideà teorii Einsteina jest to, ˝e grawitacja sta-

nowi konsekwencj´ zakrzywienia czasoprzestrzeni, która jest
powiàzana z g´stoÊcià zawartej w niej materii i energii. S∏oƒ-

ce przyciàga Ziemi´, zakrzywiajàc otaczajàcà jà czasoprze-
strzeƒ. Gdy nie ma ani materii, ani energii, oznacza to, ˝e nie
ma ˝adnego zakrzywienia, a tym samym grawitacji. Jednak
w wielowymiarowej teorii zwiàzek mi´dzy krzywiznà prze-
strzeni a g´stoÊcià wyglàda inaczej. Dodatkowe wymiary
wprowadzajà do równaƒ cz∏on korekcyjny, który sprawia, ˝e
krzywizna pustej brany nie jest zerowa. W rezultacie uciecz-
ka grawitonów wytwarza w branie wewn´trzne napr´˝enie,
nadajàce jej nieusuwalnà krzywizn´, niemajàcà zwiàzku z za-
wartà w niej materià i energià.

W miar´ up∏ywu czasu, gdy g´stoÊç materii i energii spa-

da, wywo∏ane przez nie zakrzywienie przestrzeni tak˝e male-
je, a zatem owa nieusuwalna krzywizna staje si´ coraz bardziej
dominujàca. W ten sposób krzywizna WszechÊwiata dà-
˝y do pewnej wartoÊci sta∏ej. Z podobnym zjawiskiem mieli-
byÊmy do czynienia, gdyby WszechÊwiat by∏ wype∏niony jakàÊ
substancjà, której g´stoÊç nie maleje z czasem. Taka substan-

54

ÂWIAT NAUKI MARZEC 2004

GRAFIKA BRY

AN CHRISTIE

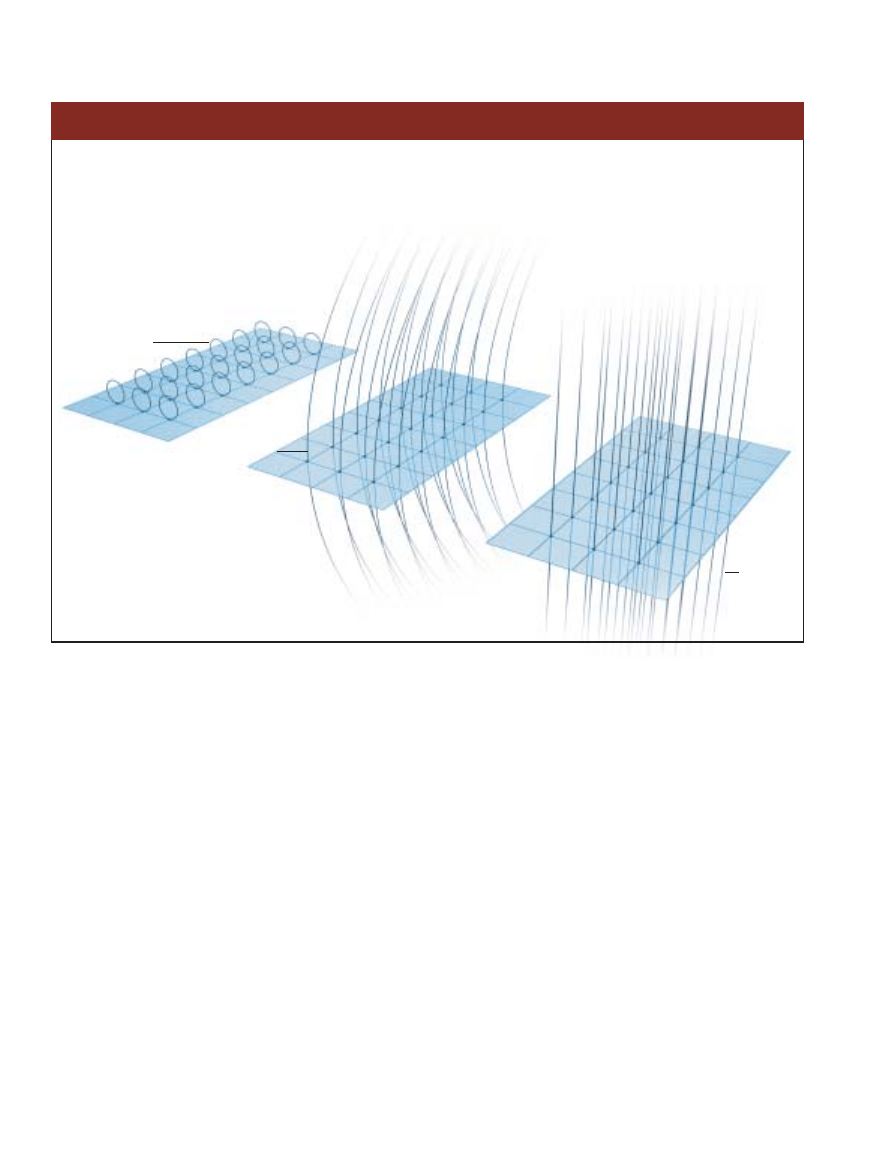
SPOLARYZOWANA BRANA

BRAK GRAWITONÓW. Gdy nie ma grawitonów,
wirtualne czàstki sà u∏o˝one chaotycznie
i nie wytwarzajà si∏y grawitacyjnej.

GRAWITON PROSTOPAD¸Y. Poruszajàc
si´ do lub z brany, grawiton powoduje
uporzàdkowanie, czyli „polaryzacj´”
czàstek wirtualnych. Spolaryzowane
czàstki generujà si∏´ grawitacji, która
przeciwstawia si´ ruchowi grawitonu.

GRAWITON RÓWNOLEG¸Y. Gdy grawiton porusza si´
w obr´bie brany, nie wywiera ˝adnego wp∏ywu
na czàstki wirtualne, poniewa˝ dzia∏a na nie
si∏à prostopad∏à do brany. Z kolei czàstki wirtualne
nie hamujà w tym przypadku ruchu grawitonu.

GRAWITONY wcale nie majà niczym nieograniczonej swobody wa∏´sania si´ po dodatkowych wymiarach. Nasz trójwymiarowy
WszechÊwiat, czyli brana (pokazana tutaj jako p∏aszczyzna) a˝ kipi od „wirtualnych” czàstek, które pojawiajà si´ i znikajà.
Jeden ze sposobów opisania ich wp∏ywu na grawitony polega na rozwa˝aniu ich jako sparowanych. Jedna z czàstek ka˝dej
pary obdarzona jest energià dodatnià (niebieski), a druga ujemnà (czerwony). Pary tego rodzaju sà w stanie nie dopuÊciç
do wchodzenia i wychodzenia grawitonów z brany.

Grawiton

Brana

cja to nic innego, jak sta∏a kosmologiczna. Dlatego nieusu-
walne zakrzywienie brany równowa˝ne jest sta∏ej kosmologicz-
nej, przyÊpieszajàcej ekspansj´ WszechÊwiata.

Nasza teoria nie jest jedynà, która postuluje odejÊcie od

konwencjonalnego prawa grawitacji na du˝ych odleg∏oÊciach.
W 2002 roku Thibault Damour i Antonios Papazoglou z
francuskiego Institut des Hautes Etudes Scientifiques oraz
Ian Kogan z University of Oxford wysun´li tez´, ˝e istnieje do-
datkowy rodzaj grawitonów, który – w przeciwieƒstwie do zwy-
k∏ych grawitonów – ma pewnà niewielkà mas´. Fizycy wie-
dzà jednak od dawna, ˝e jeÊli grawitony majà mas´, grawitacja
nie spe∏nia prawa odwrotnych kwadratów. Grawitony o nie-
zerowej masie sà niestabilne i stopniowo ulegajà rozpadowi,
co daje mniej wi´cej taki sam efekt, jak ucieczka grawitonów
– grawitony przemierzajàce du˝e odleg∏oÊci znikajà, grawita-
cja s∏abnie, a ekspansja WszechÊwiata ulega przyÊpieszeniu.
Sean Carroll, Vikram Duvvuri i Michael Turner z University of
Chicago oraz Mark Trodden z Syracuse University dokonali
modyfikacji teorii Einsteina w trzech wymiarach, wprowa-
dzajàc drobne cz∏ony odwrotnie proporcjonalne do krzywiz-
ny czasoprzestrzeni. Cz∏ony tego rodzaju by∏yby zanied-
bywalnie ma∏e we wczesnym WszechÊwiecie, lecz póêniej
wywo∏ywa∏yby przyÊpieszenie ekspansji. Równie˝ inne grupy
badawcze proponowa∏y rewizj´ prawa grawitacji, lecz ich pro-
pozycje nie eliminowa∏y koniecznoÊci odwo∏ania si´ do ciem-
nej energii jako êród∏a kosmologicznego przyÊpieszenia.

Prezent od natury

OBSERWACJE

ostatecznie rozstrzygnà, który z tych modeli jest

w∏aÊciwy. Jednego z bezpoÊrednich testów dostarczajà prze-
glàdy supernowych. PrzejÊcie od hamowania do przyÊpie-
szania wyglàda zupe∏nie inaczej w modelu ucieczki grawi-
tonów ni˝ w innych modelach, opartych na ciemnej energii.
Dalsze zwi´kszenie precyzji przeglàdów pozwoli na weryfi-
kacj´ tych teorii.

Inny test empiryczny oparty jest na obserwacji ruchu planet.

Fala grawitacyjna, podobnie jak zwyk∏a fala elektromagne-
tyczna, mo˝e mieç wyró˝niony kierunek oscylacji. Ogólna teo-
ria wzgl´dnoÊci dopuszcza dwa takie kierunki, lecz w alter-
natywnych teoriach grawitacji jest ich wi´cej. Te dodatkowe
mo˝liwoÊci modyfikujà oddzia∏ywania grawitacyjne w nie-
znaczny, lecz wyraêny sposób, pozwalajàc na wyliczenie mo˝-
liwych do zaobserwowania poprawek do ruchu planet. Wraz
z Andreiem Gruzinovem i Matiasem Zaldarriagà z New York
University wyliczy∏em, ˝e ucieczka grawitonów wywo∏a∏aby
powolnà precesj´ orbity Ksi´˝yca. Po ka˝dym pe∏nym obiegu
orbity punkt najwi´kszego zbli˝enia Ksi´˝yca do Ziemi ule-
ga∏by przesuni´ciu o oko∏o jednà bilionowà stopnia, czyli mniej
wi´cej 0.5 mm.

Ruch ten jest na tyle du˝y, ˝e da∏oby si´ go zaobserwowaç

w eksperymentach telemetrycznych, polegajàcych na moni-
torowaniu orbity Ksi´˝yca poprzez odbijanie wiàzek lasero-
wych od zwierciade∏ pozostawionych na powierzchni Ksi´˝y-
ca przez astronautów z misji Apollo. Pomiary telemetryczne
majà obecnie dok∏adnoÊç rz´du 1 cm, dlatego Eric Adelberger
i jego wspó∏pracownicy z University of Washington proponu-
jà zastosowanie laserów o wi´kszej mocy, pozwalajàcych zwi´k-
szyç t´ czu∏oÊç dziesi´ciokrotnie. Aparatura telemetryczna
umieszczona na sondach mog∏aby próbowaç znaleêç analo-
gicznà precesj´ orbity Marsa.

Ju˝ sam fakt, ˝e obserwatorzy rozprawiajà o testowaniu teo-

rii strun, jest niezmiernie ekscytujàcy. Przez lata uwa˝ano, ˝e
dotyczy ona skali bardzo ma∏ej – tak ma∏ej, ˝e nigdy nie b´dzie
jej mo˝na zweryfikowaç eksperymentalnie. PrzyÊpieszanie eks-
pansji WszechÊwiata to niebywa∏a okazja podarowana nam
przez natur´, aby zajrzeç w dodatkowe wymiary, których nor-
malnie nie jesteÊmy w stanie obserwowaç. Mo˝e si´ ona oka-
zaç pomostem mi´dzy ultrama∏ymi i superwielkimi skalami
we WszechÊwiecie. Niewykluczone zatem, ˝e losy WszechÊwia-
ta zawis∏y w∏aÊnie na strunie jak na w∏osku.

n

MARZEC 2004 ÂWIAT NAUKI

55

GRAFIKA BRY

AN CHRISTIE

The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest

for the Ultimate Theory. Brian Greene; W. W. Norton, 2003.

An Alternative to Compactification. Lisa Randall i Raman Sundrum; Phy-

sical Review Letters, tom 83, nr 23, s. 4690-4693; 6 XII 1999. Dost´p-
ny w Internecie pod adresem: http://arXiv.org/abs/hep-th/9906064

The Accelerated Universe from Gravity Leaking to Extra Dimensions.

Cédric Deffayet, Gia Dvali i Gregory Gabadadze; Physical Review D,
tom 65, numer artyku∏u 044023; 2002.

The Accelerated Universe and the Moon. Gia Dvali, Andrei Gruzinov

i Matias Zaldarriaga; Physical Review D, tom 68, numer artyku∏u 024012;
2003. http://arXiv.org/abs/hep-ph/0212069

JEÂLI CHCESZ WIEDZIEå WI¢CEJ

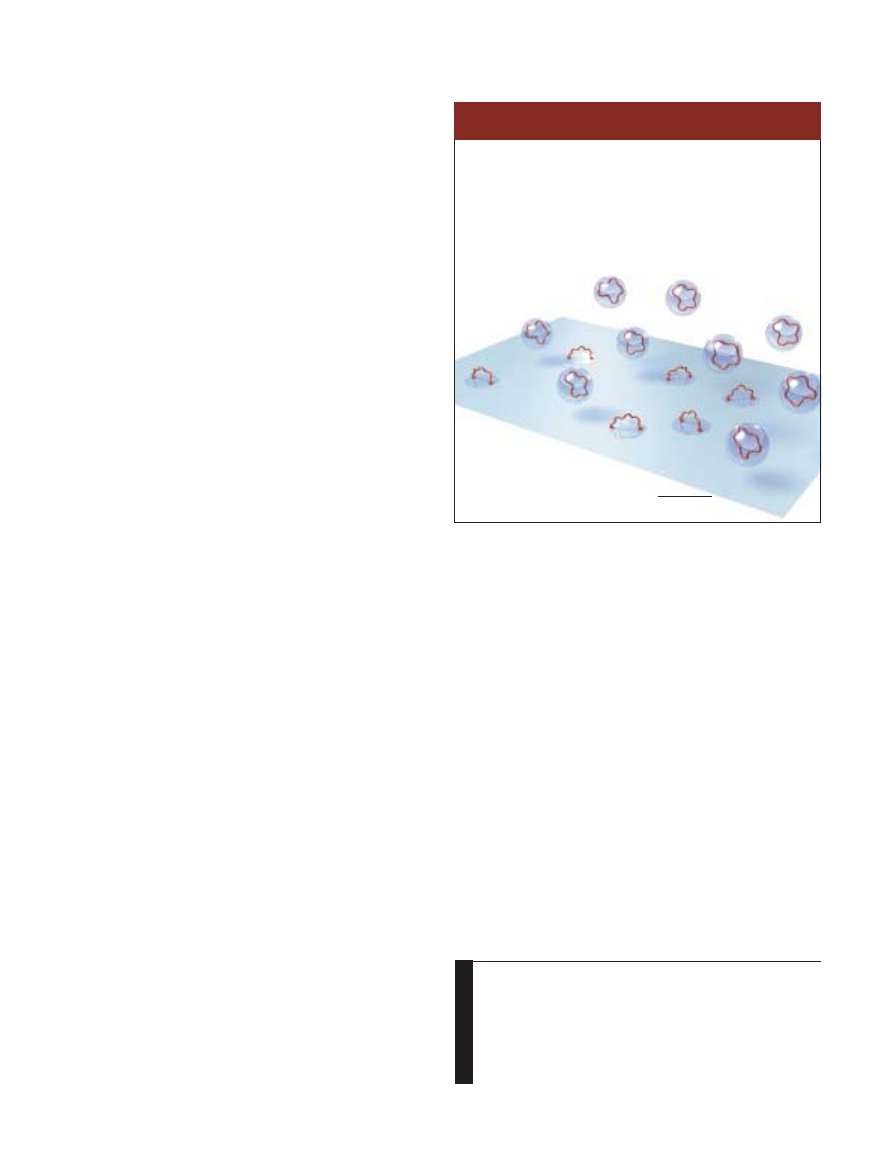
GRAWITACJA DALEKO I BLISKO

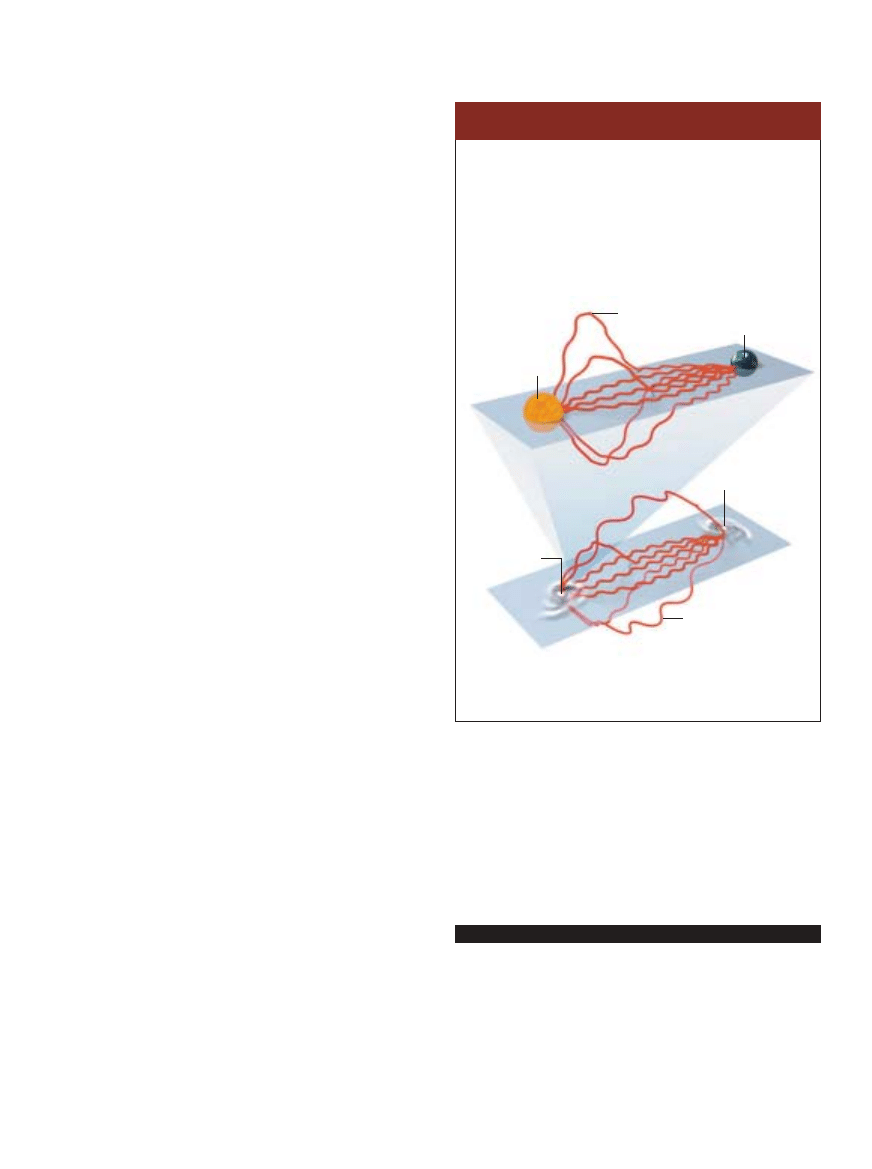
CZÑSTKI NASZEGO WSZECHÂWIATA na ogó∏ unicestwiajà
grawitony, lecz tylko wtedy, gdy grawitony majà wystarczajàcà
energi´, aby wywo∏aç ich reakcj´. Niskoenergetyczne
grawitony (o du˝ej d∏ugoÊci fali) wchodzà i wychodzà
z brany bez przeszkód.

S∏oƒce wywiera na Ziemi´ si∏´, emitujàc wirtualne grawitony
o stosunkowo ma∏ej d∏ugoÊci fali (du˝a energia), nie mogà
one zatem opuÊciç brany. Zachowujà si´ tak, jak gdyby
dodatkowe wymiary nie istnia∏y.

Odleg∏e galaktyki emitujà grawitony o du˝ej d∏ugoÊci fali
(niskoenergetyczne), które bez przeszkód przedostajà si´
do dodatkowych wymiarów. Prawo grawitacji ulega zmianie,
os∏abiajàc przyciàganie si´ galaktyk.

S∏oƒce

Galaktyka

Galaktyka

Ziemia

Grawiton
niemogàcy
opuÊciç brany

Grawiton swobodnie
wylatujàcy i wlatujàcy
do brany