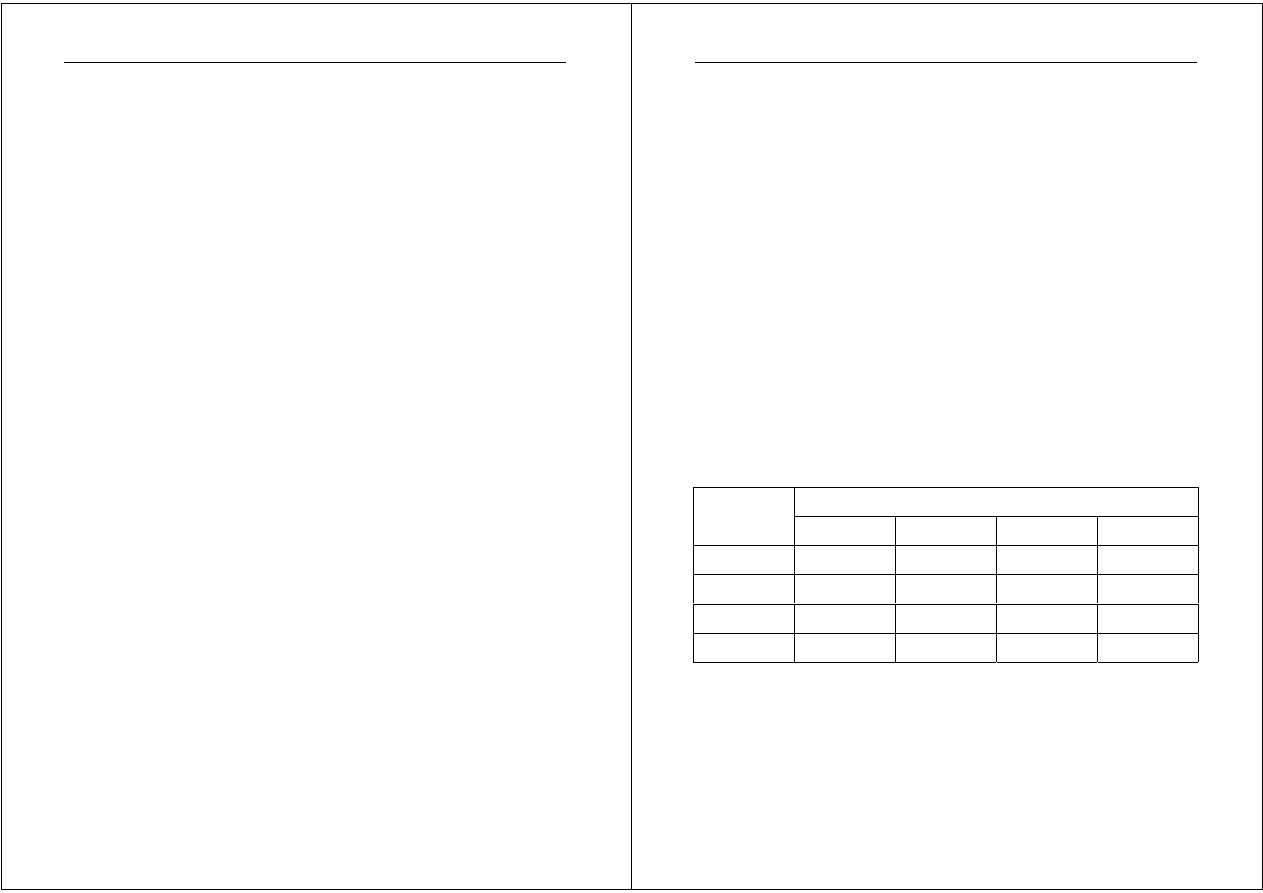
Badania operacyjne

dr inż. W. Zalewski

49

GRY I STRATEGIE

Własność sytuacji decyzyjnych, w których można wykorzystać teorię gier:

•

Istnieje skończona liczba uczestników gry (zarówno zainteresowanych

jak i nie zainteresowanych w jej wyniku);

•

Każdy uczestnik dysponuje skończoną liczbą sposobów działania;

•

Uczestnicy muszą znać wszystkie sposoby działania innych

uczestników, nie wiedząc jednak, które z nich zostaną wybrane;

•

Każdej kombinacji sposobów działania wszystkich uczestników

odpowiada określona korzyść płynąca z gry;

•

Korzyść uczestnika gry zależy zarówno od jego działania, jak i od

działania pozostałych uczestników;

•

Wszystkie możliwe wyniki gry dadzą się wyliczyć.

Sytuacja odpowiadająca powyższym warunkom nazywana jest grą.

Istnieje wiele klasyfikacji gier. W dalszej części wykładu

przedstawione zostaną gry dwuosobowe o sumie wypłat zero oraz gry

z naturą.

Badania operacyjne

dr inż. W. Zalewski

50

Gry dwuosobowe o sumie wypłat zero

W grze bierze udział dwóch graczy (ostrożnych i inteligentnych):

gracz A i gracz B. Każdy z nich ma możliwość samodzielnego

i niezależnego podejmowania decyzji. Gracz A ma ich n, a gracz B – m.

Dla każdej pary (i, j) decyzji graczy A i B znana jest pewna liczba a

ij

oznaczająca wygraną gracza A w przypadku, gdy gracz ten podejmie

decyzję i przy podjęciu przez gracza B decyzji j.

! Macierz złożoną z elementów [a

ij

] nazywamy macierzą

wypłat gracza A.

! Jeżeli liczba a

ij

oznacza jednocześnie wielkość wygranej

gracza A i wielkość przegranej gracza B, to mówimy, że
gra jest grą dwuosobową o sumie zero.

Decyzja gracza B

Decyzje

gracza A

d

B1

d

B2

d

Bm

d

A1

a

11

a

12

a

1m

d

A2

a

21

a

22

a

2m

a

ij

d

An

a

n1

a

n2

a

nm

Celem gry jest zmaksymalizowanie wygranej przez gracza A

i zminimalizowanie przegranej przez gracza B.

HACKED BY VIPER :)

Badania operacyjne

dr inż. W. Zalewski

51

Możliwe są dwie sytuacje:

1. Istnieje w grze punkt równowagi (nazywany również punktem

siodłowym), tzn. gracz A realizuje swoją możliwie największą wygraną

przy decyzji d

i

, gdy gracz B realizuje swoją możliwie najmniejszą

stratę, podejmując decyzję d

j

, przy czym obaj są zainteresowani, aby

nie zmieniać swoich decyzji. Wiedzą też jednocześnie, ile będzie

wynosiła ich wygrana (przegrana). Wielkość wygranej nazywa się

wartością gry.

! Strategią czystą nazywamy taką podjętą przez gracza

decyzję, która podejmowana jest tylko raz.

Kryterium von Neumanna (Walda):

! gracz A wybiera decyzję d

Ai

, dla której:

{ }

ij

j

a

min

przyjmuje wartość maksymalną.

! gracz B wybiera decyzję d

Bj

, dla której:

{ }

ij

i

a

max

przyjmuje wartość minimalną.

Jeżeli decyzje gracza A i B prowadza do tej samej wartości wygranej, to

gra ma punkt siodłowy. Jeżeli wartość ta wynosi 0 to jest to gra

sprawiedliwa.

Badania operacyjne

dr inż. W. Zalewski

52

2. Punkt równowagi nie istnieje i gracze nie mogą wyznaczyć dla siebie

decyzji, o których wiedzą z góry, że są dla nich obu najlepsze.

! Strategią mieszaną nazywamy liniową kombinację

wypukłą strategii czystych.

Oznacza to, że gracz postanawia stosować wszystkie lub kilka

z dostępnych mu sposobów działania w pewnej ustalonej proporcji.

Przez strategię mieszaną gracza A rozumiemy wektor X

T

=[x

1

, x

2

, ..., x

n

]

liczb rzeczywistych spełniających warunek:

x

1

+ x

2

+ ... + x

n

= 1

Przez strategię mieszaną gracza B rozumiemy wektor Y

T

=[y

1

, y

2

, ..., y

m

]

liczb rzeczywistych spełniających warunek:

y

1

+ y

2

+ ... + y

m

= 1

Elementy x

i

i y

j

przedstawiają odpowiednio częstości

(prawdopodobieństwa) z jakim gracz A wybiera i-ty spsoób postępowania

a B j-ty sposób postępowania.

Strategie mieszane stosuje się w przypadku, gdy gra nie ma punktu

siodłowego. Gdy istnieje w grze punkt równowagi, to strategią optymalna

jest strategia czysta.

HACKED BY VIPER :)

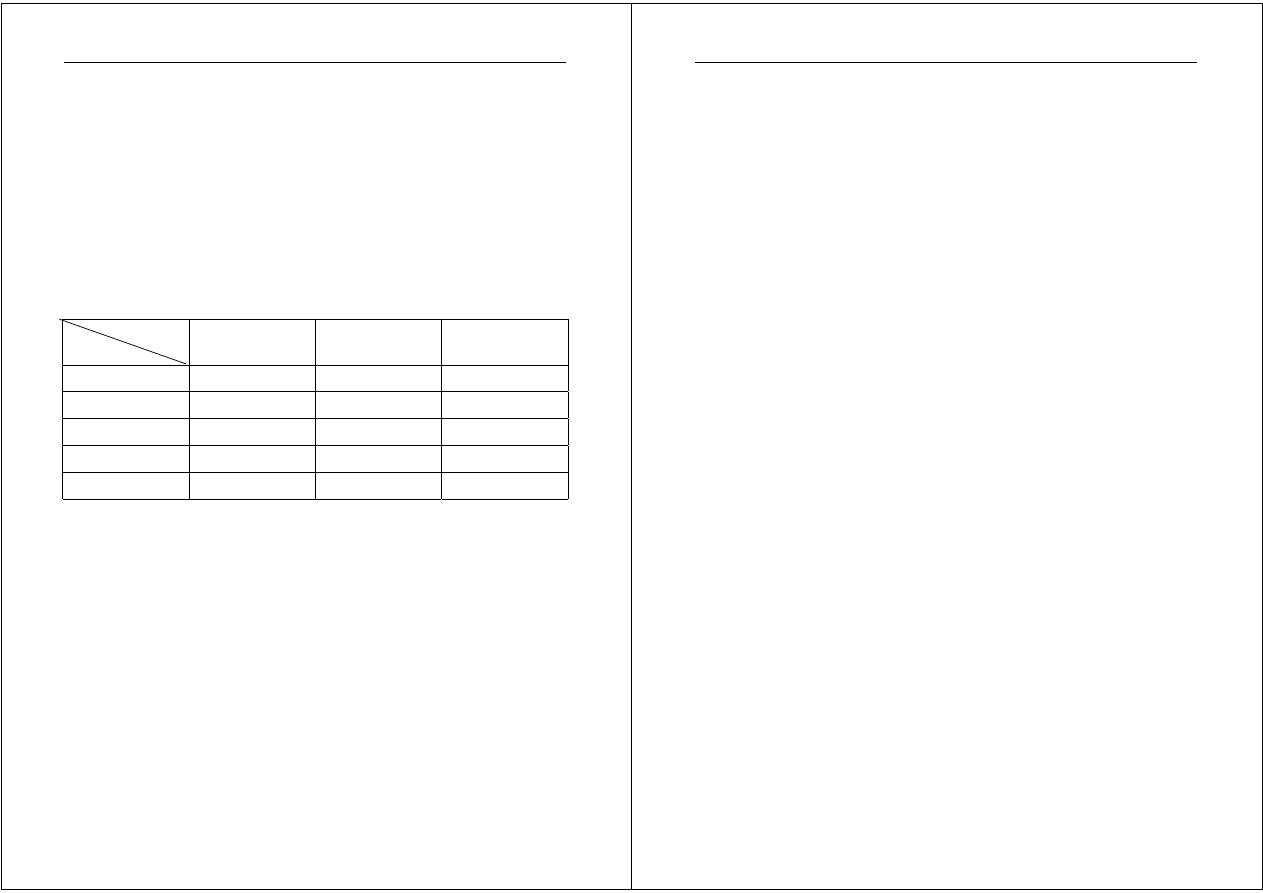
Badania operacyjne

dr inż. W. Zalewski

53

Gry z naturą

Gry

z

naturą rozgrywane są przy założeniu pasywnej postawy

drugiego gracza. Celem drugiego gracza (natury) nie jest zwycięstwo.

Rozpatrzmy przykład:

Pan Ryszard Olnik (R.Olnik) musi podjąć jesienią decyzję, którym

zbożem ma obsiać pole. Decyzję podejmuje na podstawie wiadomości
z przeszłości o wysokości plonów w zależności od warunków
atmosferycznych panujących wiosną i rodzaju zboża.

Warunki

Rodzaj zboża

Susza Normalne Deszcze

Zboże 1 24

28

36

Zboże 2

31 30 28

Zboże 3

28

34

29

Zboże 4

27

29

33

Zboże 5

31 30 29

Pan Ryszard (Olnik zresztą) musi odpowiedzieć na pytanie: którym

rodzajem zboża należałoby obsiać zboże, aby uzyskać największe plony?

Pasywna postawa drugiego gracza (natury) wymusza zmianę

reguł podejmowania decyzji. Stosuje się cztery kryteria:

! reguła maxmin,

! Laplace’a (Bayesa),

! Hurwicza,

! Savage’a.

Badania operacyjne

dr inż. W. Zalewski

54

1. Reguła maxmin.

Zasada podobna do reguły von Neumanna – podejmuje się decyzję,

która pozwoli osiągnąć maksymalną wygraną spośród minimalnych.

Szukamy takiego i

0

, dla którego:

{ }

ij

j

i

0

i

a

min

max

a

=

W przypadku pana R. Olnika prowadzi to do wyboru minimalnej

wartości w każdym wierszu macierzy wypłat i wybraniu z nich wartości

maksymalnej. Tzn. 24, 28, 28, 27, 29

"

max = 29

"

Optymalną decyzją

jest decyzja d

5

.

2. Reguła Laplace’a.

Wszystkie

przyszłe stany natury mogą wystąpić z prawdo-

podobieństwem p

j

. Na tej podstawie możliwe jest wyliczenie wartości

oczekiwanej rezultatów każdej decyzji.

Szukamy takiego i

0

, dla którego:













=

∑

j

j

ij

i

i

p

a

E

max

0

Jeżeli założymy, że prawdopodobieństwo wystąpienia stanu „Suszy”

wynosi 0,3; „Normalnego” – 0,5; „Deszczu” – 0,2; otrzymamy sumę

wiersza pierwszego: 24*0,3+28*0,5+36*0,2=28,4 W przypadku pana R.

Olnika prowadzi to do wyboru maksymalnej wartości spośród sum w

poszczególnych wierszach. Tzn. 28,4; 29,9; 31,2; 29,2 30,1

"

max = 31,2

"

Optymalną decyzją jest decyzja d

3

.

HACKED BY VIPER :)

Badania operacyjne

dr inż. W. Zalewski

55

3. Reguła Hurwicza

Decyzją optymalną jest decyzja, dla której otrzymujemy wartość

maksymalną wyrażenia:

d

i

=

α

A

i

+ (1 –

α

)a

i

,

gdzie

α

– współczynnik skłonności do ryzyka

α

∈

<0, 1>,

{ }

ij

j

i

a

min

a

=

{ }

ij

j

i

a

A

max

=

W przypadku pana R. Olnika prowadzi to do następującego wyboru.

Jeżeli przyjęty poziom ufności wynosi 0,25 (poziom ryzyka 0,75)

poszczególne parametry przyjmą wartości:

{ }

ij

j

i

a

min

a

=

{ }

ij

j

i

a

A

max

=

d

i

=

α

A

i

+ (1 –

α

)a

i

d

i

24

36

0,75*36

+

0,25*24

33,0

28

31 0,75*31 + 0,25*28

30,25

28

34

0,75*34

+

0,25*28

25,0

27

33

0,75*33

+

0,25*27

31,5

29

31 0,75*31 + 0,25*29

30,5

Maksymalna

wartość spośród sum w poszczególnych wierszach

wynosi max = 33,0

"

Optymalną decyzją przy poziomie ufności 0,25 (lub

poziomie ryzyka 0,75) jest decyzja d

1

.

Badania operacyjne

dr inż. W. Zalewski

56

4. Reguła Savage’a

Dla

każdego ze stanów natury z osobna, a następnie dla każdej

możliwej decyzji wyznaczamy wielkość utraconych korzyści, które

moglibyśmy osiągnąć (w stosunku do decyzji najlepszej przy danym stanie

natury). Następnie postępujemy zgodnie z regułą von Neumanna,

uwzględniając, że mamy do czynienia z wielkościami niepożądanymi

(spośród wartości maksymalnych wybieramy minimalną).

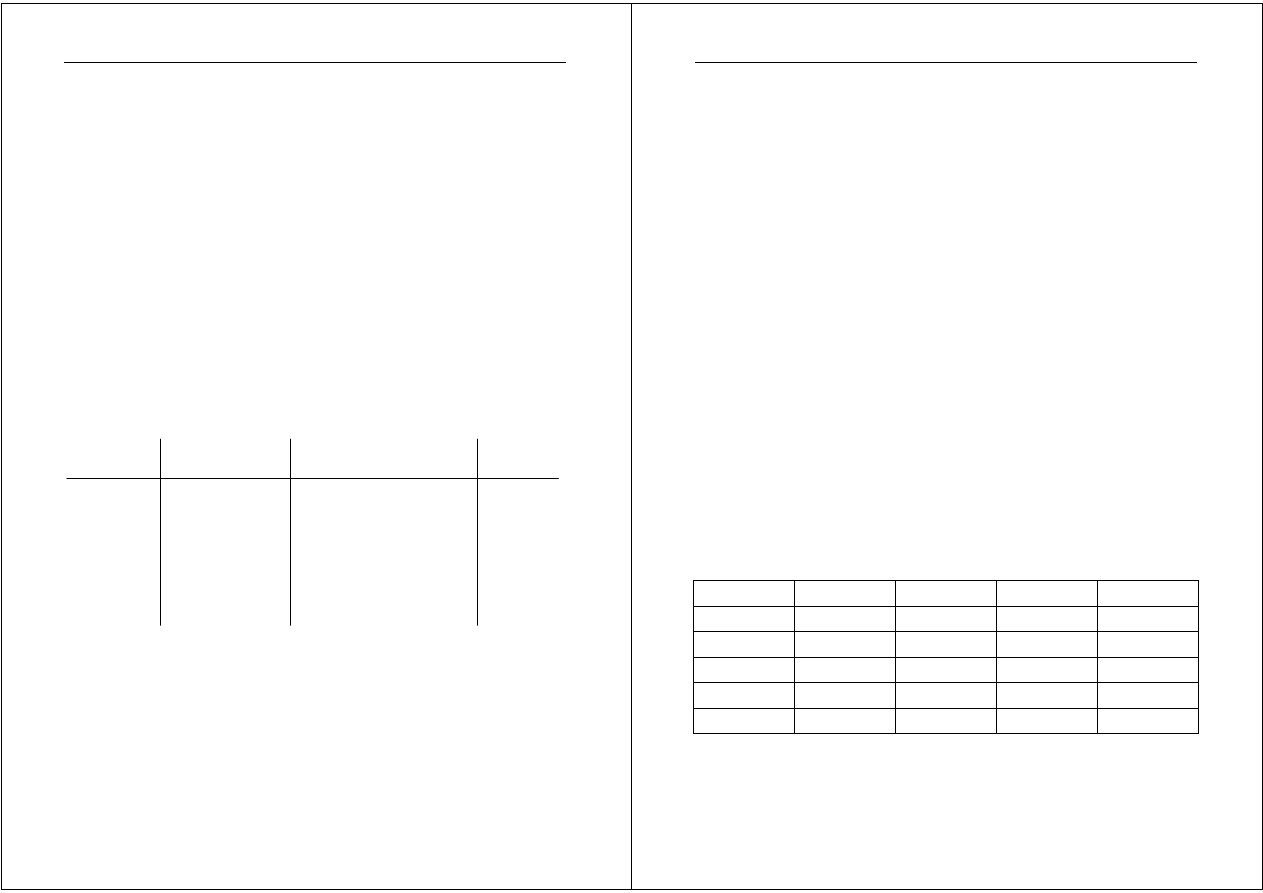
Krok I – tworzymy macierz „żalu”, której elementy definiuje się jako:

R = {r

ij

},

gdzie

{ }

ij

ij

i

ij

a

a

max

r

−

=

Krok II – szukamy elementu maksymalnego w każdym wierszu,

a następnie elementu minimalnego spośród nich, który wyznaczy decyzję

optymalną. Szukamy takiego i

0

, dla którego:

{ }

ij

j

i

0

i

r

max

min

R

=

W przypadku pana R. Olnika prowadzi to do następującego wyboru.

Wartości maksymalne w poszczególnych kolumnach wynoszą: 31, 34, 36.

Wyznaczamy macierz „żalu”:

S

1

S

2

S

3

R

0

Z

1

31 – 24 = 7

6

0

7

Z

2

0 4 8 8

Z

3

3 0 7 7

Z

4

4 5 3 5

Z

5

0 4 7 7

Minimalna wartość spośród maksymalnych wartości w poszczególnych

wierszach wynosi min = 5

"

Optymalną decyzją jest decyzja d

4

HACKED BY VIPER :)