1. Sformułuj twierdzenie Bernoulliego o ciągu monotonicznym i ograniczonym i udowodnij.
Definicja twierdzenia Bernoulliego

: Każdy ciąg który jest monotoniczny i ograniczony jest zbieżny. Jego

granicą jest dolny kres zbioru wartości (w przypadku ciągu malejącego lub nierosnącego) albo górny kres zbioru
wartości (w przypadku ciągu rosnącego lub niemalejącego).

Dowód:

(a)Ciąg

rosnący

i

ograniczony

, np. ciąg 𝑎

𝑛

=

𝑛

𝑛+1

(mogą być też inne przykłady: 𝑎

𝑛

= −

1

𝑛

, 𝑎

𝑛

= −2

−𝑛

Najpierw dowód na to że ciąg ten jest rosnący: Badamy znak wyrażenia 𝑎

𝑛+1

− 𝑎

𝑛

:

𝑎

𝑛+1

− 𝑎

𝑛

=

𝑛 + 1

𝑛 + 1 + 1

−

𝑛

𝑛 + 1

=

𝑛 + 2 − 1

𝑛 + 2

−

𝑛 + 1 − 1

𝑛 + 1

= 1 −

1

𝑛 + 2

− 1 −

1

𝑛 + 1

= −

1

𝑛 + 2

+

1

𝑛 + 1

=

=

𝑛 + 2 − (𝑛 + 1)

𝑛 + 1 𝑛 + 2

=

1

𝑛 + 1 𝑛 + 2

Numer wyrazu 𝑛 jest zawsze dodatni (pierwszy wyraz, drugi wyraz, dziesiąty, czy nawet milionowy), więc:
skoro 𝑛 > 0, 𝑡𝑜 𝑛 + 1 > 0 oraz 𝑛 + 2 > 0 oraz skoro 𝑛 > 0 to także

1

𝑛

> 0 i analogicznie

1

𝑛+1

> 0 oraz

1

𝑛+2

> 0 (własności

funkcji hiperbolicznej) tak więc iloczyn dwóch liczb dodatnich

1

𝑛+1 𝑛+2

> 0, więc 𝑎

𝑛+1

− 𝑎

𝑛

> 0. Każdy następny

wyraz jest większy od poprzedniego, więc ciąg jest rosnący.
Teraz dowód na to że ten ciąg jest ograniczony:
Skoro:

1

𝑛

>

1

𝑛+1

>

1

𝑛+2

> ⋯ > 0, to −

1

𝑛

< −

1

𝑛+1

< −

1

𝑛+2

< ⋯ < 0, czyli:

𝑎

𝑛

=

𝑛

𝑛+1

=

𝑛+1−1

𝑛 +1

= 1 −

1

𝑛 +1

< 1 −

1

𝑛+2

< 1 −

1

𝑛+3

< ⋯ < 1 − 0 = 1, więc ciąg jest ograniczony z góryprzez liczbę 1, bo

każdy wyraz tego ciągu, jest mniejszy od 1. Faktycznie: lim

𝑛→∞

𝑎

𝑛

= lim

𝑛 →∞

𝑛

𝑛+1

= lim

𝑛→∞

1 −

1

𝑛+1

=

= lim

𝑛→∞

1 − lim

𝑛→∞

1

𝑛+1

= 1 −

1

∞+1

= 1 − 0 = 1, co jest granicą ciągu i jednocześnie asymptotą poziomą tej funkcji (dla

każdej funkcji monotonicznie rosnącej i ograniczonej granica funkcji w ∞ jest zarazem jej asymptotą poziomą)
(b)Ciąg

malejący

i

ograniczony

, np.𝑏

𝑛

=

1

𝑛

(mogą być też inne przykłady: 𝑏

𝑛

= −

𝑛

𝑛+1

, 𝑏

𝑛

= 2

−𝑛

)

Najpierw dowód na to że ciąg ten jest rosnący: Badamy znak wyrażenia 𝑏

𝑛+1

− 𝑏

𝑛

:

𝑏

𝑛+1

− 𝑏

𝑛

=

1

𝑛 + 1

−

1
𝑛

=

𝑛 − 𝑛 + 1

𝑛 𝑛 + 1

=

−1

𝑛 𝑛 + 1

Numer wyrazu 𝑛 jest zawsze dodatni, więc −𝑛 jest zawsze ujemny, czyli: 𝑛 > 0 → −𝑛 < 0,

−1

𝑛 𝑛 +1

=

−1

𝑛

∙

1

𝑛+1

, więc skoro −𝑛 < 0, 𝑡𝑜 −

1

𝑛

< 0 oraz skoro 𝑛 > 0, 𝑡𝑜 𝑛 + 1 > 0, 𝑤𝑖ę𝑐

1

𝑛+1

> 0, więc

𝑏

𝑛+1

− 𝑏

𝑛

=

−1

𝑛 𝑛 +1

=

−1

𝑛

∙

1

𝑛+1

< 0 (iloczyn liczby zawsze ujemnej −

1

𝑛

przez zawsze dodatnią

1

𝑛+1

daje liczbę zawsze

ujemną). Każdy następny wyraz ciągu jest mniejszy od poprzedniego, wiec ciąg jest malejący.
Teraz dowód na to że ten ciąg jest ograniczony:
Wiadomo że: 𝑏

1

> 𝑏

2

> 𝑏

3

> 𝑏

4

> 𝑏

5

> ⋯, czyli

1

𝑛

>

1

𝑛 +1

>

1

𝑛+2

>

1

𝑛+3

>

1

𝑛+4

> ⋯ a wiemy że ten granica tego ciągu wyraża

się w ten sposób:

1

𝑛

>

1

𝑛+1

>

1

𝑛+2

>

1

𝑛+3

>

1

𝑛+4

> ⋯ >

1

𝑛+∞

=

1

∞

= 0, inaczej:

lim

𝑛→∞

1
𝑛

=

1

∞

= 0

2. Wyjaśnij termin co to jest relacja równoważności i podaj 4 przykłady.

Relacje równoważności

nazywamy relacjędwuargumentową R,𝑹 ⊂ 𝒂, 𝒃 : 𝒂, 𝒃 ∈ 𝑨 , którą jest w zbiorze A:

Zwrotna

:

∀

𝑥∈𝐴

𝑥𝑅𝑥,

Symetryczna

:

∀

𝑥,𝑦∈𝐴

(𝑥𝑅𝑦) → (𝑦𝑅𝑥),

Przechodnia

:

∀

𝑥,𝑦,𝑧∈𝐴

(𝑥𝑅𝑦)˄(𝑦𝑅𝑧) → (𝑥𝑅𝑧),

Przykłady tej relacji

:

W zbiorze wszystkich trójkątów:

podobieństwo trójkątów, przystawanie trójkątów;

W zbiorze prostych:

równoległość (oznaczenie ||);

W każdym zbiorze:

równość elementów (oznaczenie =);

W zbiorze 𝑍 liczb całkowitych:

kongruencja, czyli przystawanie modulo 𝑚 (dla ustalonej liczby 𝑚 > 1 o

dwóch liczbach mówimy, że są równe modulo 𝑚, jest ich różnica jest całkowitą wielokrotnością liczby 𝑚);

W zbiorze 𝑅 liczb rzeczywistych:

równość modulo 2𝜋 (dwie liczby nazywamy równymi modulo 2𝜋, jeśli ich

różnica jest całkowitą wielokrotnością liczby 2𝜋);

Relację równoważności

zapisuje się 𝒔𝒚𝒎𝒃𝒐𝒍𝒆𝒎 ~ (tylda, znak podobieństwa figur, proporcjonalności), lub ≡

(znak identyczności, przystawania figur lub właśnie równoważności)

3. Podaj definicję geometryczną i analityczną iloczynu wektorowego i podaj przykłady.

4. Wyznacz granicę gdzie 𝐥𝐢𝐦

𝒙→𝟎

(𝒔𝒊𝒏𝒄 𝒙).

Mamy tzw. okrąg jednostkowy (kąt 𝑥 w radianach, promień

okręgu 𝑟 = 1, więc 𝑂𝐴 = 𝑂𝐵 = 1, w ∆𝑂𝐴𝐵 wysokością jest

odcinek 𝑦, 𝑥 to długość łuku – poniżej pokażę dlaczego wychodzi

to akurat 𝑥, skoro 𝑥 to wartość kąta w radianach, oraz z

odcinkiem 𝑂𝐴 tworzą kąt prosty)

C

Z funkcji trygonometrycznych kąta x:

𝑦

𝑂𝐵

= sin 𝑥, 𝑎 𝑠𝑘𝑜𝑟𝑜 𝑂𝐵 = 1, 𝑤𝑖ę𝑐 𝑦 = sin 𝑥

𝑧

𝑂𝐴

= 𝑡𝑔 𝑥 𝑖 𝑡𝑎𝑘 𝑠𝑎𝑚𝑜 𝑧 = 𝑡𝑔 𝑥

Długość łuku:

𝑥

2𝜋

∙ 2𝜋𝑟 = 𝑥𝑟 = 𝑥 ∙ 1 = 𝑥

Teraz mamy do wyboru 2 sposoby, oba honorowane przez Marleya:

I sposób (ten Marleyowy z wykładów) – porównywanie długości odcinków/łuków:

Jak widzimy na rysunku , zachodzą podane zależności długości boków:
𝑦 < 𝑥 < 𝑧 czyli sin 𝑥 < 𝑥 < 𝑡𝑔 𝑥,

II sposób (mój pomysł, podobny do tego na filmiku z YT):

Porównując pola trójkątów wg wzoru: 𝑆

∆

=

1

2

𝑎𝑕

𝑎

, otrzymujemy poniższe wzory i zależności:

𝑆

∆𝑂𝐴𝐵

=

1
2

𝑂𝐴 ∙ 𝑦 =

1
2

sin 𝑥

Pole wycinka koła 𝐴𝐵

:

𝑆 =

𝑥

2𝜋

∙ 𝜋𝑟

2

=

1
2

𝑥𝑟

2

=

1
2

𝑥

𝑆

∆𝑂𝐴𝐶

=

1
2

𝑂𝐴 ∙ 𝑧 =

1
2

𝑡𝑔 𝑥

I zależności pól tych figur: 𝑺

∆𝑶𝑨𝑩

< 𝑆 < 𝑺

∆𝑶𝑨𝑪

, czyli

𝟏

𝟐

𝐬𝐢𝐧 𝒙 <

𝟏

𝟐

𝒙 <

𝟏

𝟐

𝒕𝒈 𝒙, więc 𝐬𝐢𝐧 𝒙 < 𝑥 < 𝑡𝑔 𝑥

Tu się kończy ten drugi sposób, i dalej:
wiemy że 𝑡𝑔 𝑥 =

sin 𝑥

cos 𝑥

, więc:

sin 𝑥 < 𝑥 <

sin 𝑥

cos 𝑥

, dzielimy stronami dany układ nierówności przez sin 𝑥

1 <

𝑥

sin 𝑥

<

1

cos 𝑥

Teraz korzystając z własności: 3 >

1

2

; ale odwracając do góry nogami każdą z tych liczb musimy

zamienićznakinierówności na przeciwne, więc wychodzi

1

3

< 2, co w naszym układzie nierówności przyjmuje

postać:

1 >

sin 𝑥

𝑥

> cos 𝑥

tutaj korzystamy z

twierdzenia o trzech ciągach

, więc:

skoro: 1 >

sin 𝑥

𝑥

> cos 𝑥, to: lim

𝑥→0

1 > lim

𝑥→0

sin 𝑥

𝑥

> lim

𝑥→0

cos 𝑥

1 > lim

𝑥→0

sin 𝑥

𝑥

> cos 0 = 1

1 > lim

𝑥→0

sin 𝑥

𝑥

> 1

na podstawie twierdzenia o trzech ciągach
𝐥𝐢𝐦

𝒙→𝟎

𝐬𝐢𝐧 𝒙

𝒙

=1

5. Uzyskaj równanie prostej która jest stycznia do hiperboli o równaniu

𝒙

𝟐

𝒂

𝟐

−

𝒚

𝟐

𝒃

𝟐

= 𝟏 w punkcie (𝒙

𝟎

, 𝒚

𝟎

)

(niesprawdzone)
Przede wszystkim, jest to równanie hiperboli w postaci kanonicznej, inaczej, jest równanie hiperboli w postaci

uwikłanej (postać jawna to taka z której łatwo otrzymać postać 𝑦 = 𝑓(𝑥), w uwikłanej mamy 𝐹(𝑥, 𝑦)). Skoro do

otrzymania stycznej do funkcji w punkcie (𝑥

0

, 𝑦

0

) trzeba policzyć pochodną funkcji i wstawić do wzoru

𝑦 − 𝑦

0

= 𝑓′(𝑥

0

)(𝑥 − 𝑥

0

)

To do funkcji uwikłanej trzeba policzyć pochodne cząstkowe względem x i względem y (każde osobno) i
podstawiamy do wzoru:

𝐹

𝑥

′

𝑥

0

, 𝑦

0

∙ 𝑥 − 𝑥

0

+ 𝐹

𝑦

′

(𝑥

0

, 𝑦

0

) ∙ (𝑦 − 𝑦

0

) = 0

Więc: 𝐹(𝑥, 𝑦) =

𝑥

2

𝑎

2

−

𝑦

2

𝑏

2

− 1

𝐹

𝑥

′

𝑥, 𝑦 =

2𝑥

𝑎

2

𝐹

𝑦

′

𝑥, 𝑦 = −

2𝑦

𝑏

2

𝑥 − 𝑥

0

∙

2𝑥

0

𝑎

2

+ 𝑦 − 𝑦

0

∙ −

2𝑦

0

𝑏

2

= 0

𝑥 − 𝑥

0

∙

2𝑥

0

𝑎

2

= 𝑦 − 𝑦

0

∙

2𝑦

0

𝑏

2

𝑥 − 𝑥

0

∙

𝑥

0

𝑦

0

∙

𝑏

2

𝑎

2

= 𝑦 − 𝑦

0

𝑦 =

𝑥

0

𝑦

0

∙

𝑏

2

𝑎

2

∙ 𝑥 −

𝑥

0

2

𝑦

0

∙

𝑏

2

𝑎

2

+ 𝑦

0

6. Sformułuj twierdzenie diagonalizacji i je udowodnij.

Diagonalizacja to rozkład macierzy polegający na rozbiciu macierzy kwadratowej 𝐴 ∈ 𝑀

𝑘

(𝐾)na iloczyn macierzy:𝑃, ∆, 𝑃

−1

∈ 𝑀

𝑘

(𝐾)

𝐴 = 𝑃∆𝑃

−1

Gdzie ∆jest macierzą diagonalną, 𝑃, 𝑃

−1

są nazywane macierzami przejścia.

Współczynniki na głównej przekątnej macierzy diagonalnej 𝛥 są równe kolejnym wartościom własnym macierzy A, z kolei
kolumny macierzy P stanowią kolejne wektory własne macierzy A.
𝜒

𝑎

(𝜆)=det(A-𝜆)=(−1)

𝑛

(𝜆

𝑛

+ 𝑐

𝑛−1

𝜆

𝑛−1

+ ⋯ + 𝑐

1

𝜆 + 𝑐

0)

gdzie 𝑐

0

− 𝑑𝑒 𝑡 𝐴 𝑐

1

− 𝑡𝑟 𝐴 =

𝑎

𝑗𝑗

𝑛

𝑗 =1

Macierze kwadratowe, które można przedstawić w postaci diagonalnej, nazywamy diagonalizowalnymi.

7. Przedstaw związek pomiędzy 0xy i 0rθ w układzie ortokartezjańskim i biegunowym oraz wyznacz
jakobian przejścia jednego równania w drugie.

Skoro mowa tu o układzie biegunowym to chodzi o układy dwuwymiarowe (w trzech wymiarach, jego
odpowiednikiem jest układ współrzędnych sferycznych).
Układem współrzędnych kartezjańskich nazywa się układ
współrzędnych, w którym zadane są:
• punkt zwany początkiem układu współrzędnych, którego
wszystkie współrzędne są równe zeru, często oznaczany literą O
lub cyfrą 0
• zestaw n parami prostopadłych osi liczbowych zwanych osiami układu współrzędnych. Dwie pierwsze osie
często oznaczane są jako:
• (pierwsza oś, zwana osią odciętych),
• (druga, zwana osią rzędnych),
Układ współrzędnych biegunowych:
Każdemu punktowi P płaszczyzny przypisujemy jego współrzędne
biegunowe jak następuje:
• promień wodzący punktu P to jego odległość |𝑂𝑃| od bieguna
• amplituda punktu P to wartość kąta skierowanego pomiędzy półprostą𝑂𝑃

OS a wektorem

Dla jednoznaczności przyjmuje się, że 0 ≤ 𝜑 < 2𝜋 wspołrzędne bieguna O są równe.

Związki i przejście z jednego układu do drugiego

Przejście z układu biegunowego do ortokartezjańskiego:

𝑟 ≥ 0, 𝜑 ∈< 0,2𝜋)

𝑥 = 𝑟 ∙ cos 𝜑

𝑦 = 𝑟 ∙ sin 𝜑

Przejście z układu ortokartezjańskiego do biegunowego.

𝑟 = 𝑥

2

+ 𝑦

2

Jakobian przejścia do współrzędnych ortokartezjańskich

𝐷 𝑥, 𝑦
𝐷 𝑟, 𝜑

=

𝜕𝑥
𝜕𝑟

𝜕𝑥

𝜕𝜑

𝜕𝑦

𝜕𝑟

𝜕𝑦

𝜕𝜑

=

cos 𝜑

−𝑟 sin 𝜑

sin 𝜑

𝑟 cos 𝜑

=

= 𝑟 ∙ cos 𝜑

2

− −𝑟 sin 𝜑

2

= 𝑟(cos

2

𝜑 + sin

2

𝜑) = 𝑟

8. Podaj definicje geometryczna i analityczna iloczynu skalarnego w przestrzeni 𝑹

𝟐

oraz przedstaw

gdzie ten iloczyn występuje.
Iloczyn skalarny

(inaczej

iloczynwewnętrzny

). Wynikiem takiego iloczynu jest

skalar

– wielkość

niewektorowa, czyli po prostu wartość. Geometrycznie iloczyn skalarny𝒂

∘ 𝒃

wyraża się jako długość rzutu

prostokątnego jednego wektora na drugi. Iloczyn skalarny wektorów 𝒂

i 𝒃

definiuje się jako:

𝒂

∘ 𝒃

= 𝒂 𝒃 𝒄𝒐𝒔(𝜸)

*** gdzie 𝜸jest rozwartością kąta między 𝒂

oraz 𝒃

. Iloczyn skalarny można zapisać jako:

𝒂

∘ 𝒃

= 𝒂

𝟏

𝒃

𝟏

𝒊 + 𝒂

𝟐

𝒃

𝟐

𝒋 + 𝒂

𝟑

𝒃

𝟑

𝒌

ogólnie:𝒂

∘ 𝒃

=

𝒂

𝒊

𝒃

𝒊

𝒏

𝒊=𝟏

𝒕

𝒊

. gdzie 𝑖 , 𝑗 , 𝑘 ,𝑡

𝑖

to wektory jednostkowe wzdłuż osi

odpowiednio OX, OY, OZ i i-tej osi układu współrzędnych n-wymiarowych

Iloczyn wektorowy

(nazywany również

iloczynem zewnętrznym

) ma sens jedynie w trzech wymiarach.

Różni się on od iloczynu skalarnego głównie tym, że wynikiem iloczynu wektorowego dwóch wektorów jest
wektor. Iloczyn wektorowy𝒂

× 𝒃

jest wektorem prostopadłym tak do 𝒂

jak i do 𝒃

i jest zdefiniowany jak

𝒂

× 𝒃

= 𝒂 𝒃 𝐬𝐢𝐧 𝜽 𝒏

***gdzie θ jest rozwartością kąta między 𝒂

oraz 𝒃

, a n jest wektorem jednostkowym prostopadłym jednocześnie

do𝒂

i𝒃

, który uzupełnia układ prawoskrętny. Ograniczenie prawoskrętności jest niezbędne, ponieważ istnieją dwa

wektory jednostkowe, które są równocześnie prostopadłe do𝒂

i 𝒃

, mianowicie 𝒏

oraz -𝒏

.

***Iloczyn wektorowy𝒂

× 𝒃

jest określony tak, by 𝒂

, 𝒃

i 𝒂

× 𝒃

również były układem prawoskrętnym (jednakże

𝒂

oraz 𝒃

nie muszą być koniecznie ortogonalne). Jest to tzw. reguła prawej dłoni. Długość 𝒂

× 𝒃

może być

interpretowana jako pole równoległoboku o bokach a oraz b. Iloczyn wektorowy może być zapisany jako:

𝒂

× 𝒃

= 𝒂

𝟐

𝒃

𝟑

− 𝒂

𝟑

𝒃

𝟐

𝑖 + 𝒂

𝟑

𝒃

𝟏

− 𝒂

𝟏

𝒃

𝟑

𝑗 + 𝒂

𝟏

𝒃

𝟏

− 𝒂

𝟐

𝒃

𝟐

𝑘 =

𝑎

1

𝑏

1

𝑖

𝑎

2

𝑏

2

𝑗

𝑎

3

𝑏

3

𝑘

9. Podaj definicję szeregu liczbowego i jego sumy, zbieżności i zbieżności względnej oraz przykłady.

Szereg

𝑎

𝑛

∞

𝑛=1

nazywamy zbieżnym bezwzględnie, jeżeli zbieżny jest szereg

𝑎

𝑛

∞

𝑛=1

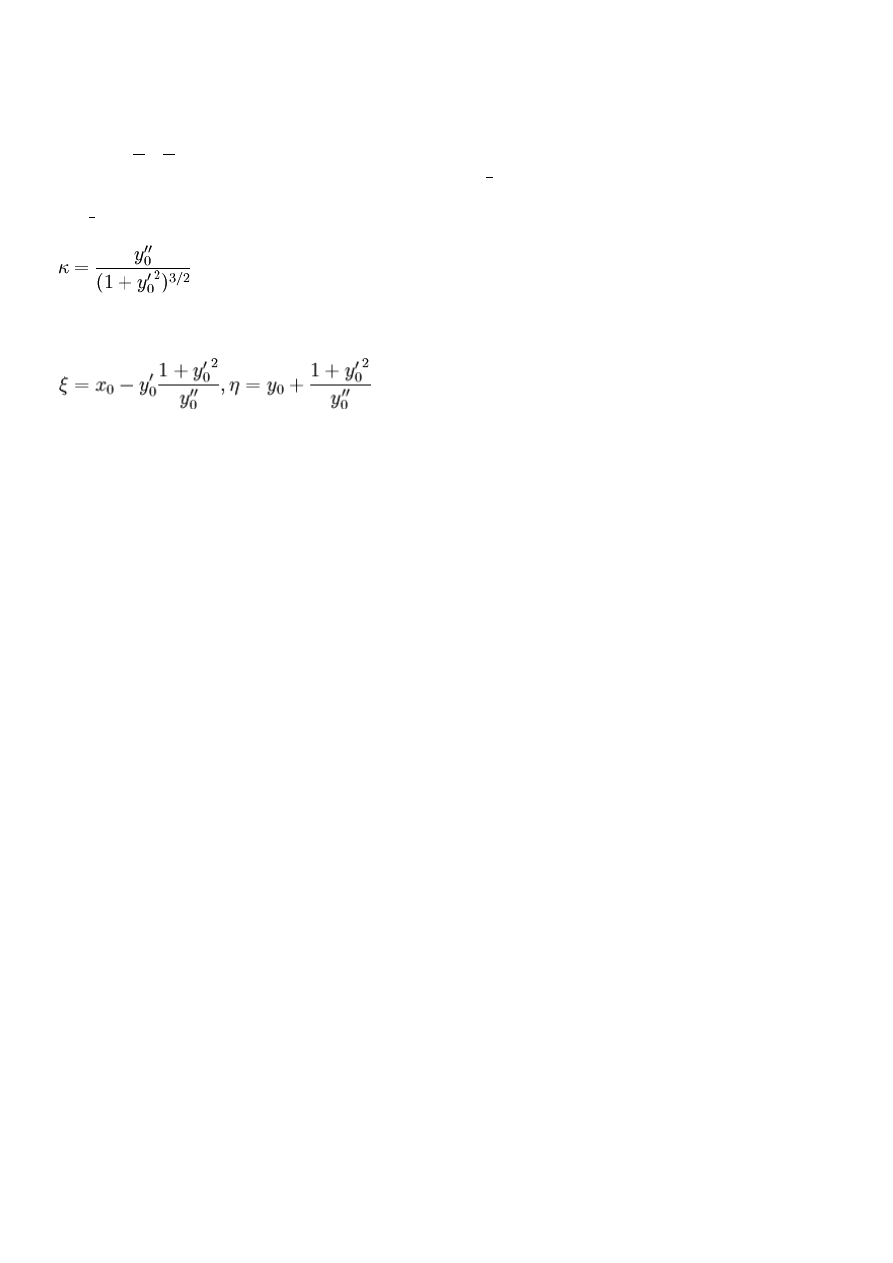
Zwykła: Jeśli wyraz ogólny 𝑎

𝑛

szeregu

𝑎

𝑛

∞

𝑛=1

nie zbiega do 0, symbolicznie lim

𝑛 →∞

𝑎

𝑛

≠ 0

10. Zdefiniuj pojęcie krzywizny krzywej o równaniu 𝒚 = 𝒇(𝒙) i podaj wzór.
Krzywiznę krzywej płaskiej κ

(grecka litera Kappa) definiuje się jako:

𝜅 = 𝑙𝑖𝑚

∆𝑆→0

∆𝜌

∆𝑆

=

𝑑𝜌

𝑑𝑆

, gdzie ∆𝑆 jest długością łuku (i dąży do zera) a ∆𝜌 jest kątem pod jakim przecinają się styczne

do tej krzywej na końcach łuku. Dla okręgu 𝜅 = 𝑐𝑜𝑛𝑠𝑡. 𝑜𝑟𝑎𝑧 𝜅 =

1

𝑅

, 𝑐𝑧𝑦𝑙𝑖, 𝜅 ≥ 0 gdzie R to promień tegoż okręgu.

Każdą krzywą można określić jako sumę łuków okręgów, toteż promień krzywizny w danym punkcie wynosi:
𝛿 =

1

𝜅

. Dla prostej przyjmuje się promień dążący do nieskończoności, co daje krzywiznę równą zero. Dla funkcji

przedstawionej w postaci jawnej:

Koło krzywiznowe (okrąg krzywiznowy)

nazywamy okrąg który przechodząc przez punkt P danej krzywej ma

styczność z krzywą wyższego rzędu niż jakikolwiek inny okrąg przechodzący przez punkt P. Okrąg krzywiznowy

istnieje wyłącznie w tych punktach, w których nie występuje wyprostowanie krzywej (𝜅 ≠ 0). Dla krzywej o
równaniu w postaci jawnej 𝑦 = 𝑓(𝑥), środek takiego okręgu S(ξ,η) ma takie współrzędne: