Skala logarytmiczna – rodzaj

skali pomiarowej

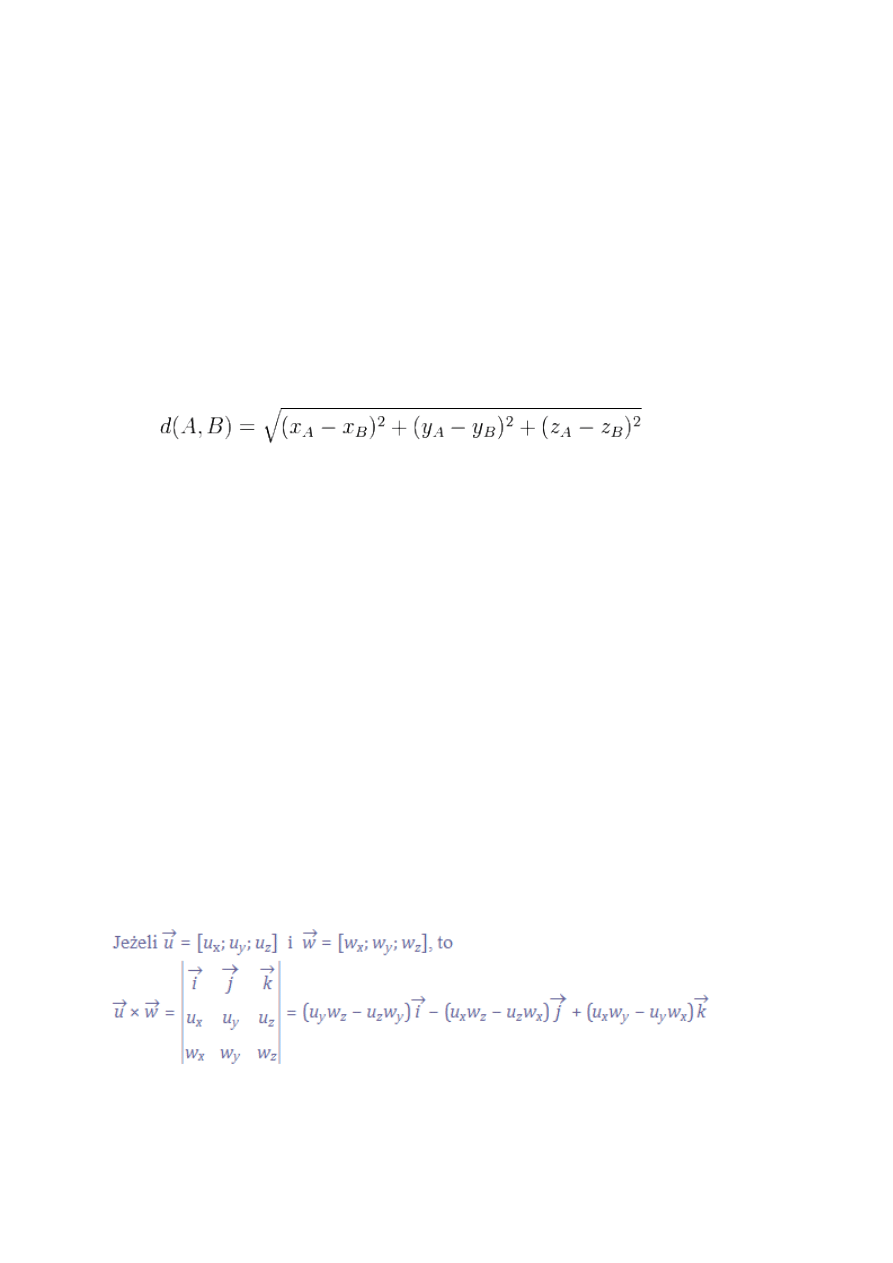
, w której mierzona wartość

wielkości fizycznej

jest przekształcana za pomocą

logarytmu

.

Wartości na skali logarytmicznej są zawsze

bezwymiarowe

, to jest albo podawane w

odniesieniu do pewnej

jednostki

, albo będące logarytmami wielkości niemianowanych. Skala

musi również mieć zdefiniowaną używaną

podstawę logarytmu

.

Układ współrzędnych –

funkcja

przypisująca każdemu

punktowi

danej

przestrzeni

(w

szczególności przestrzeni dwuwymiarowej –

płaszczyzny

, powierzchni

kuli

itp.)

skończony

ciąg

(

krotkę

)

liczb rzeczywistych

zwanych współrzędnymi punktu.

Wektor – para 2 punktów; para liczb (współrzędnych 2 punktów – 4 liczby); punkt
zaczepienia, długość wektora; kierunek, zwrot (PDKZ).
Iloczynem skalarnym 2 wektorów na płaszczyźnie nazywamy iloczyn długości jednego z
nich razy długość drugiego razy cos kąta między nimi. a*b=|a|*|b|*cosB=b*a.
Odległość euklidesowa między dwoma punktami jest równa długości

odcinka

łączącego te

punkty.

Iloczyn wektorowy – mnożenie wektorowe, operacja, której wynikiem jest nowy wektor.
Iloczynem wektorowym wektorów niezerowych u i w nazywamy wektor v taki że:
V=|u|*|w|sin(u,w); v jest wektorem prostopadłym do u i w; jego zwrot jest taki, że układ
wektorów u,w,v, ma orientację zgodną z przyjętą orientacją przestrzeni.

Iloczyn wektorowy oznaczamy: u x w = v.

Wartość iloczynu wektorowego jest równa iloczynowi długości pierwszego wektora i długości
rzutu drugiego wektora na kierunek prostopadły do pierwszego wektora.

Długość wektora otrzymanego jako iloczyn wektorowy dwóch wektorów jest równy polu
równoległoboku rozpiętego na tych wektorach.

Wektor zerowy otrzymamy wówczas, gdy jeden z wektorów wyjściowych jest zerowy lub
gdy wyjściowe wektory są równoległe. Warunek równoległości u x w = 0.

Własności iloczynu wektorowego:

u x w = - (w x u)
k(u x w) = (ku) x w = u x (kw)
(u + w) x v = u x v + w x v

Iloczyn splotowy – wynika działania określonego dla dwóch funkcji dającego w wyniku inną
funkcję, która może być postrzegana jako zmodyfikowana wersja oryginału.

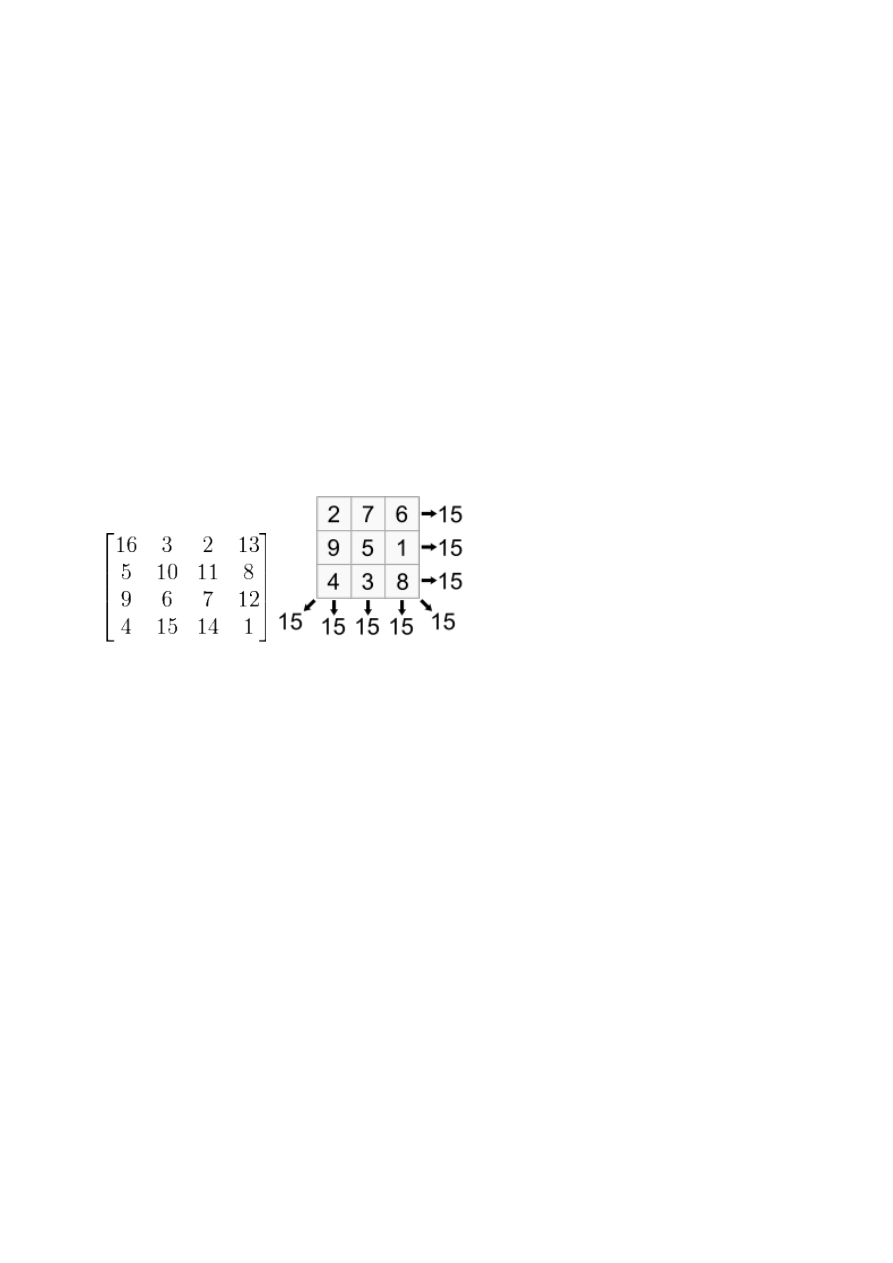
Układ współrzędnych biegunowych (układ współrzędnych polarnych) -

układ

współrzędnych

na

płaszczyźnie

wyznaczony przez pewien

punkt

O zwany biegunem oraz

półprostą

OS o początku w punkcie O zwaną

osią

biegunową.

Równania krawędziowe prostej - układ równań postaci

ax + by + cz = d,

a´x + b´y + c´z = d´,

gdzie (a,b,c) i (a´,b´,c´) są niezerowymi i nieproporcjonalnymi trójkami liczb. Układ ten
przedstawia prostą w przestrzeni trójwymiarowej, bo poszczególne równania tego układu
przedstawiają płaszczyzny prostopadłe do wektorów o współrzędnych odpowiednio (a,b,c) i
(a´,b´,c´), a nieproporcjonalność tych trójek wyklucza równoległość tych płaszczyzn.
Wspomniana prosta jest więc przedstawiona jako wspólna krawędź dwóch płaszczyzn - stąd
nazwa.

Kwadrat magiczny – tablica składająca się z n wierszy i n kolumn (n>2), w którą wpisano n

2

różnych dodatnich

liczb naturalnych

w ten sposób, że suma liczb w każdym wierszu, w

każdej kolumnie i w każdej przekątnej jest taka sama (tzw. suma magiczna).

Macierz – w

matematyce

układ liczb, symboli lub wyrażeń zapisanych w postaci prostokątnej

tablicy.

Macierzą nazywamy funkcję, która jest określona na iloczynie kartezjańskim skończonej
liczby zbiorów skończonych.

Macierz prostokątna określona jest na iloczynie kartezjańskim dwóch zbiorów, z których
pierwszy liczy m elementów, a drugi ma n elementów. Nazywa się również (m,n) macierzą
lub (mxn) macierzą.

Iloczyn kartezjański zbiorów A i B to zbiór takich wszystkich uporządkowanych par (a,b),
dla których a należy do zbioru A i b należy do zbioru B. Iloczyn kartezjański oznaczamy jako
A × B. Mnożenie kartezjańskie nie jest przemienne. Oznacza to, że zwykle A × B ≠ B × A.

Wyznacznik macierzy to funkcja określona na macierzach kwadratowych związana z
mnożeniem i dodawaniem odpowiednich elementów danej macierzy tak, by otrzymać
pojedynczą liczbę. Inaczej mówiąc wyznacznik macierzy jest to liczba rzeczywista
przyporządkowana macierzy kwadratowej. Wyznacznik oznaczamy symbolicznie detA lub |
A|.

Reguła Sarrusa to praktyczny sposób obliczania

wyznacznika

stopnia 3, gdzie skorzystanie z

rozwinięcia Laplace'a

może być niewygodne. Algorytm ten został odkryty przez francuskiego

matematyka

Pierre'a Sarrusa

.

Reguła Sarrusa nie przenosi się na wyznaczniki wyższych stopni.

Rozwinięcie

Laplace'a

- wzór

rekurencyjny

określający

wyznacznik

n-tego stopnia macierzy

kwadratowej o wymiarach

. Wyznacznik det A macierzy

znajduje się z

następującego wzoru:

gdzie:

i jest ustalone i określa wiersz macierzy, względem którego następuje rozwinięcie

- element macierzy w i-tym wierszu i j-tej kolumnie

-

dopełnienie algebraiczne

elementu

powstałe z przemnożenia czynnika ( − 1)

i +

j

przez

minor

elementu a

ij

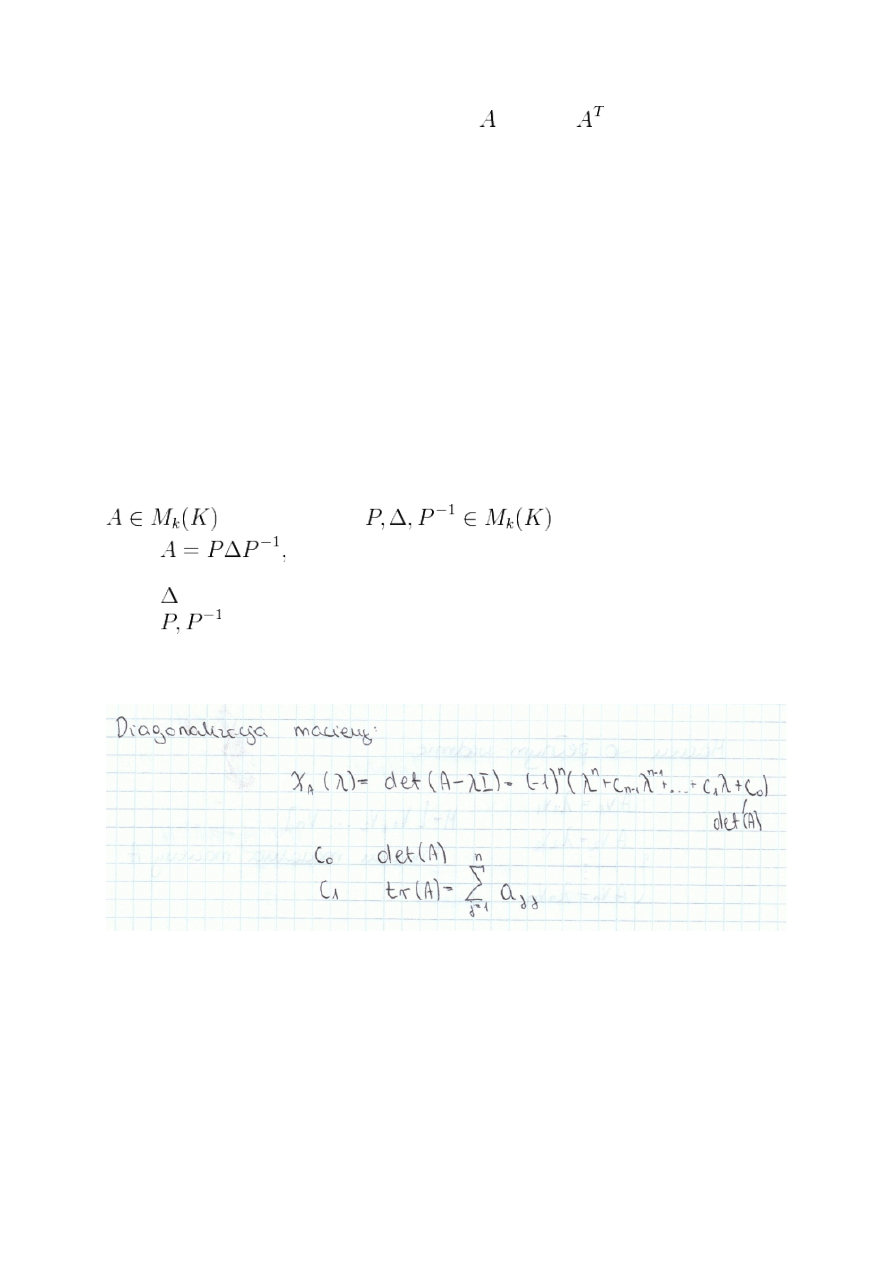
Macierz transponowana (przestawiona) macierzy to macierz

, która powstaje z danej

poprzez zamianę jej wierszy na kolumny i kolumn na wiersze. Operację tworzenia macierzy
transponowanej nazywamy transpozycją (przestawianiem).
Macierz trójkątna to

macierz kwadratowa

, której wszystkie współczynniki pod

główną

przekątną

lub wszystkie współczynniki nad tą przekątną są równe zero. Należy zauważyć, że

kwadratowa

macierz schodkowa

jest zawsze macierzą trójkątną.

Macierz diagonalna –

macierz

, zwykle kwadratowa

[1]

, której wszystkie współczynniki leżące

poza

główną przekątną

(główną diagonalą) są zerowe. Inaczej mówiąc jest to macierz

górno-

i

dolnotrójkątna

jednocześnie.

Macierz nieosobliwa=odwracalna - macierz, której wyznacznik jest różny od zera.
Macierz osobliwa=nieodwracalna - macierz, której wyznacznik jest równy zero.

Każda macierz, która nie jest kwadratowa nie jest odwracalna.
Podmacierz danej macierzy to dowolny układ jej elementów powstały przez „skreślenie”
pewnej liczby wierszy i kolumn sam tworzący macierz.
Macierz diagonalna – to taka w której wszystkie elementy oprócz przekątnej są równe zero.
a

j,k

=0; j=k.

Diagonalizacja to

rozkład macierzy

polegający na rozbiciu

macierzy kwadratowej

na

iloczyn

macierzy

:

gdzie

•

jest

macierzą diagonalną

,

•

są nazywane

macierzami przejścia

.

Współczynniki na głównej przekątnej macierzy diagonalnej Δ są równe kolejnym

wartościom

własnym

macierzy A, z kolei kolumny macierzy P stanowią kolejne

wektory własne

macierzy

A.

Macierze kwadratowe, które można przedstawić w postaci diagonalnej, nazywamy
diagonalizowalnymi.
Ural – układ równań algebraicznych.
Twierdzenie Kroneckera – Capellego
Jeżeli rząd macierzy A jest równy rzędowi macierzy rozszerzonej to układ równań ma
rozwiąznanie. W przeciwnym wypadku nie ma rozwiązań. J*rz(a)=rz[a|b].
Rzędem macierzy nazywamy największy stopień podmacierzy nieosobliwej tej macierzy.
Podmacierz danej macierzy to dowolny układ jej elementów powstały przez skreślenie
pewnej liczby wierszy lub kolumn sam tworzący macierz.

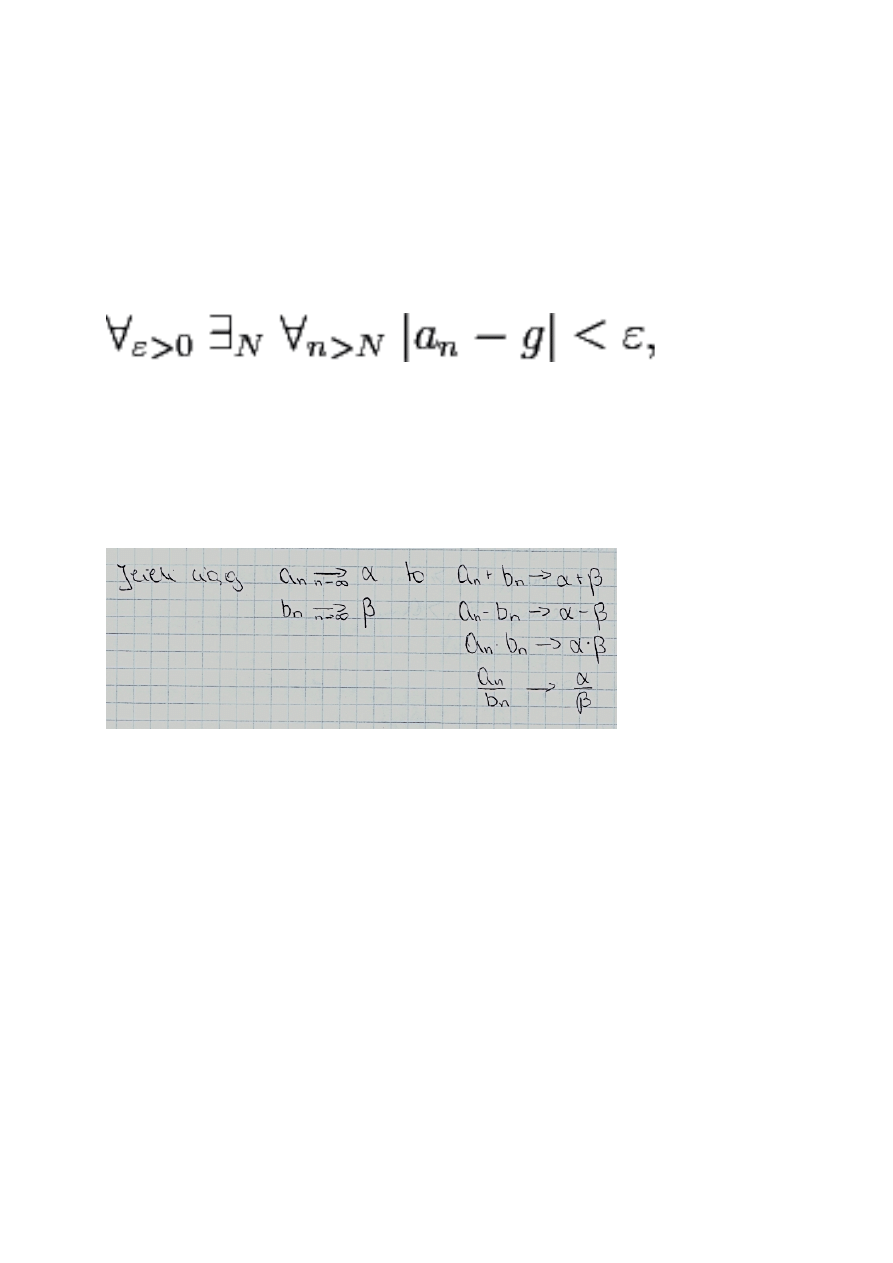
Ograniczoność ciągu
Ciąg jest ograniczony z góry jeżeli istnieje takie M że dla każdego n>n

0

: a

n

<M.

Ciąg jest ograniczony z dołu jeżeli istnieje takie M że dla każdego n≤n

0

: |a

n

|≤M.

Monotoniczność ciągu
- rosnący : a

n

<a

n+1

- niemalejący : a

n

≤an

+1

- nierosnący : a

n

≥a

n+1

- malejący : a

n

>a

n+1

Zbieżność ciągu
Liczbę g nazywa się granicą ciągu (a

n

), jeżeli

g=

Ciąg rozbieżny to ciąg, który nie jest zbieżny tzn ciąg który nie ma granicy.
Jeżeli istnieje takie g że dla każdego ε>0 (nieskończenie wiele wyrazów ciągu a

n

) d(an;g)<ε to

wówczas punkt g jest nazywany punktem skupienia.
Twierdzenie o jednoznaczności
Ciąg zbieżny ma dokładnie jedną granicę.
Twierdzenie o granicy ciągu zbieżnego.

Symbole oznaczone: ∞+∞=∞; |const/0| = ∞; |const/∞|=0.
Symbole nieoznaczone: 0/0; ∞/∞; ∞-∞; 0*∞; 0

0

; 1^∞; ∞^0.

Twierdzenie o podciągu ciągu zbieżnego:
Podciąg ciągu zbieżnego jest zbieżny (do tej samej granicy)
Twierdzenie o 3 ciągach:
Jeżeli dane są trzy ciągi ( a

n

), ( b

n

), ( c

n

) i

oraz an <= bn <=cn to =g .

Twierdzenie o ciągu rosnącym, ograniczonym z góry (dołu). Ciąg taki jest zbieżny.
Warunek konieczny zbieżności ciągu:
Ciąg zbieżny jest ograniczony ( nie zachodzi twierdzenie odwrotne).

Dla a>0 Jeżeli a>1:

Wzór dwumianowy Newtona:
Dwumian Newtona wzór zgodnie z którym

potęgę

dwumianu

(x + y)

n

można rozwinąć w

sumę

jednomianów

postaci ax

k

y

l

. W każdym z tych jednomianów współczynnik a jest

dodatnią

liczbą całkowitą

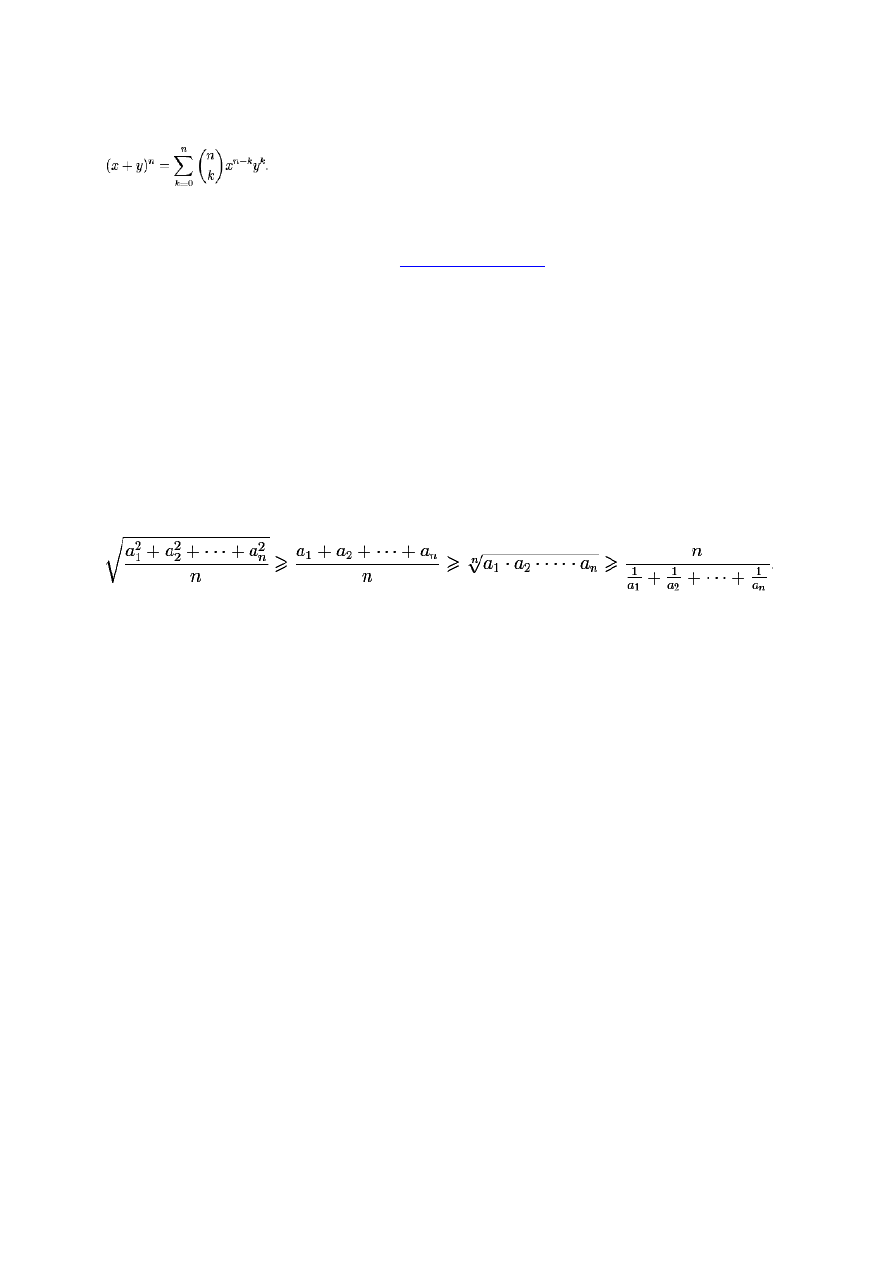
, a wykładniki przy x oraz y sumują się do n. Współczynniki a przy

jednomianach są

symbolami Newtona

i nazywane są współczynnikami dwumianowymi.

Trójkąt Pascala – trójkątna

tablica

liczb: Na bokach trójkąta znajdują się liczby 1, a

pozostałe powstają jako suma dwóch bezpośrednio znajdujących się nad nią. Liczby stojące w
n-tym wierszu to kolejne współczynniki

dwumianu Newtona

- rozwinięcia . Na przykład:

w trzecim wierszu trójkąta mamy 1, 3, 3, 1.

Twierdzenie Bernoulliego o istnieniu liczby Eulera.
Liczba e jest granicą ciągu a

n

=(1+ )

n

Czyli e=((1+ )

n

)

Dowód zbieżności:
Wykażmy że ciąg ((1+ )

n

)

nEN

jest niemalejący i ograniczony z góry, a zatem jest zbieżny.

Dla dodatnich liczb x1,x2,…,x

nr1

zachodzi nierówność między ich średnią arytmetyczną a

geometryczną.
Nierówność Cauchy'ego:
Ciąg: średnia kwadratowa, średnia arytmetyczna, średnia geometryczna, średnia harmoniczna
liczb a1,a2…an jest nierosnący. Oznacza to że:

Więc:

Rozwijając x

1

=..x

n

=1+1/n oraz x

n+1

otrzymujemy

a stąd

A więc również

Czyli ciąg jest niemalejący
Połóżmy
Z nierówności zastosowanej do oraz x

n+2

=2 otrzymujemy, że

Stąd

A więc również

Czyli ciąg jest niemalejący
Ponieważ to możemy wywnioskować, że ciąg
Ciąg a

n

jest więc niemalejący i ograniczony z góry np. przez b

1

a więc jest zbieżny.

Krzywa łańcuchowa: krzywa płaska opisująca kształt doskonale nierozciągliwej i
nieskończenie wiotkiej liny o niezerowej masie swobodnie zwisającej pomiędzy dwiema
różnymi podporami w jednorodnym polu grawitacyjnym.
Krzywa jest dana równaniem: y=acosh(x/a)

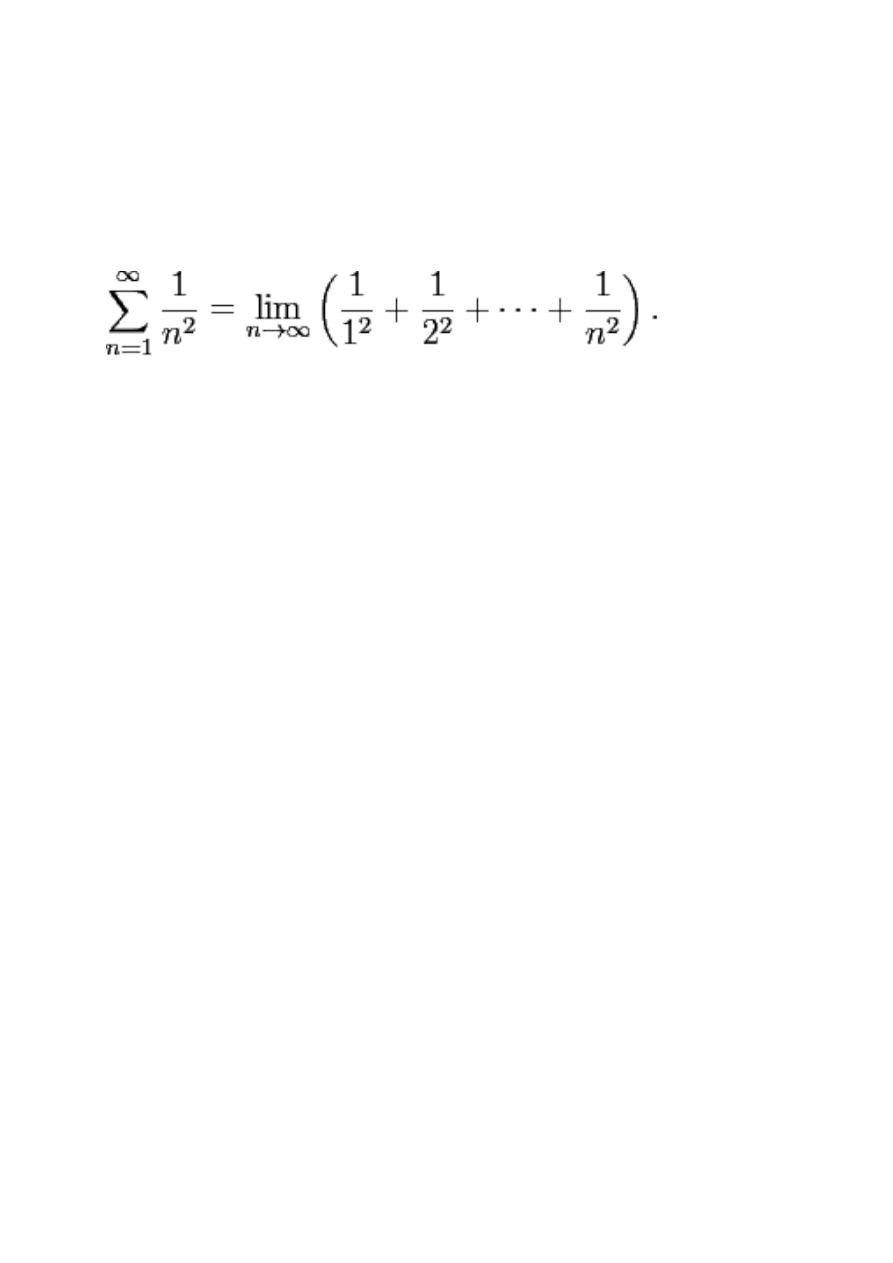
Coshx=((e^x) + (e^-x))/2 - cosinus hiperboliczny

Cykloida opisana jest równaniami parametrycznymi postaci: x=r(t-sint) ; y=r(1-cost).
Ciąg funkcyjny to ciąg, którego elementami są funkcje np.: f0,f1,f2,f3,… lub x,x^2,x^3…

Przedmiotem problemu bazylejskiego w jego pierwotnym brzmieniu było znalezienie
dokładnej sumy odwrotności kwadratów wszystkich liczb naturalnych, tj. sumy szeregu:

Suma ta z dokładnością do szóstego miejsca po przecinku wynosi 1,644934. Istotą
bazylejskiego problemu było jednak znalezienie odpowiedzi na pytanie jaka jest dokładna
suma tego szeregu i przeprowadzenie na to odpowiedniego

dowodu

. Euler w swoim odkryciu

ogłoszonym w 1735 stwierdził, że suma ta wynosi

π

2

/6. W ówczesnej argumentacji użył

pewnych zabiegów nieuprawnionych wedle wiedzy z tamtego roku; w pełni poprawny w
sensie rygorów matematycznych dowód przeprowadził w 1741.

Pochodną funkcji f(x) w punkcie x

0

nazywamy granicę (o ile istnieje):

= tg(alfa)
<tu powinien byc zajebisty wykres>

Inne zapisy: Df(x0), , (x0)

Jeżeli funkcja ma w pkt. A pochodną to mówimy, że jest w tym pkt. różniczkowalna.
poch. lewostronna
poch. prawostronna

Reguła de l’ Hospitala, tylko dla (1sza reguła) i (2ga reguła)
Zasady:
Jeżeli f i g są różniczkowalne w otoczeniu x

0

Jeżeli f, i g dążą do 0 (

∾)

To:

Monotoniczność funkcji
F(a) <
f(b)

Rosnąca

F’(x)>
0

F(a) <=
f(b)

Niemalejąc
a

F’(x)>
=0

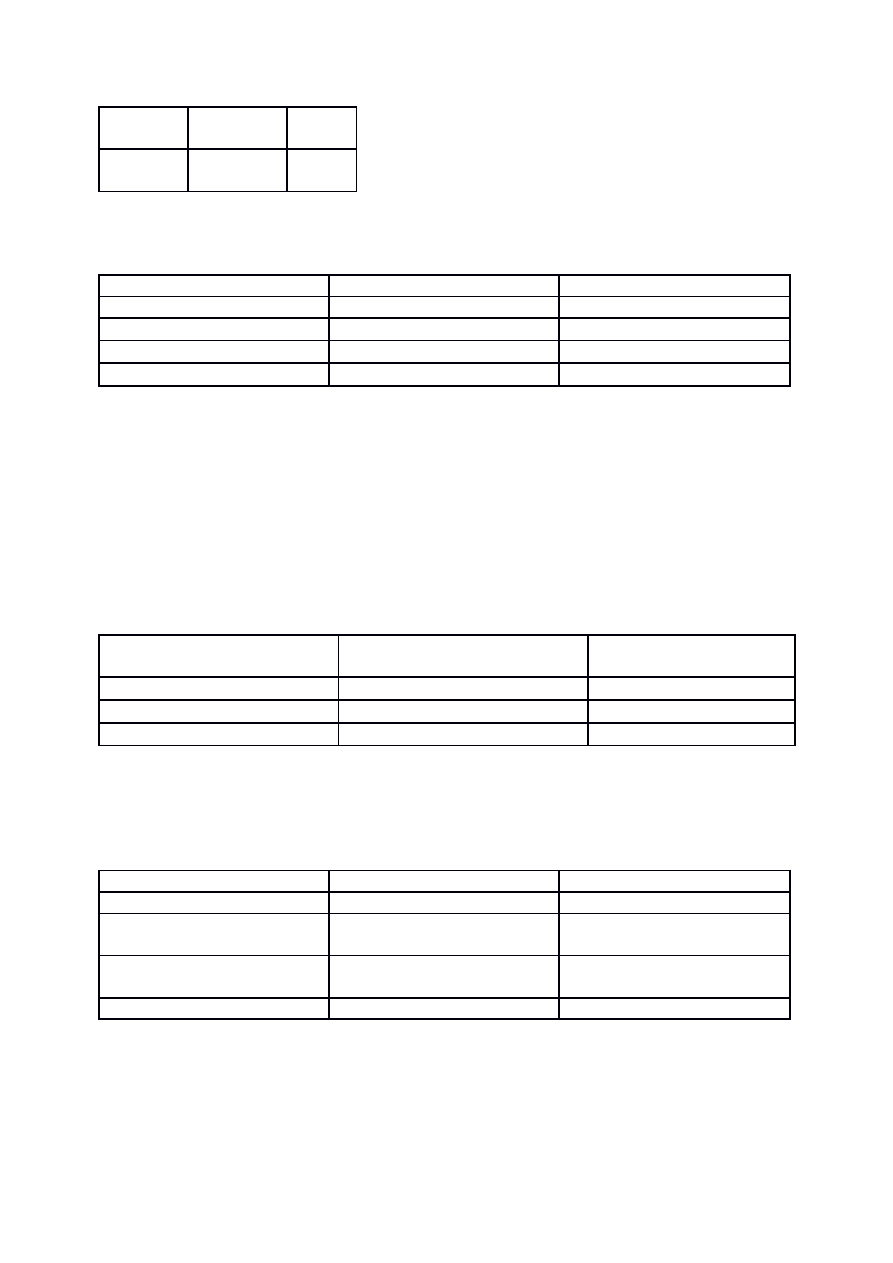
F(a) >=
f(b)

nierosnąca

F’(x)<
=0

F(a) >
f(b)

malejąca

F’(x)<
0

Jeżeli f nie jest ciągła to badamy ją tylko w przedziałach ciągłości

Ekstrema w funkcji nieliniowej
X<x0

x>x0

+

↗

+

↗

Rosnąca w całym przedziale

+

↗

-

↘

X0 maks - ekstremum

-

↘

+

↗

X0 min - ekstremum

-

↘

-

↘

Malejąca w całym przedziale

Warunek konieczny ekstremum
Jeżeli funkcja jest różniczkowalna, i ma w punkcie x0 ekstremum to znika w tym pkt
pochodna: f’(x0)=0

Uwaga: pochodna równa 0 w x0 nie oznacza, że w pkt x0 jest extremum, gdyż w punkcie x

0

musi nastąpić zmiana znaku drugiej pochodnej.

II pochodna, wypukłość i wklęsłość

Mówimy, że funkcja jest:

Wypukła

F’’>0

Wklęsła

>

F’’<0

Niewklęsła

=>

F’’>0

Niewypukła

=<

F’’>0

w dowolnym przedziale, dla każdych dowolnych 2 pkt. a i b.
Geometrycznie: f. jest np. wypukła, jeżeli wykres funkcji zawartej pomiędzy 2 dowolnymi
pkt. a i b leży poniżej siecznej wyznaczonej przez te pkt.

F’’ dla X<x0

F’’ dla x>x0

rezultat

+

+

wypukła

-

+

X0 to punkt infleksji
(przegięcia)

+

-

X0 to punkt infleksji
(przegięcia)

-

-

wklęsła

Przebieg zmienności funkcji

Argumenty
Wartości

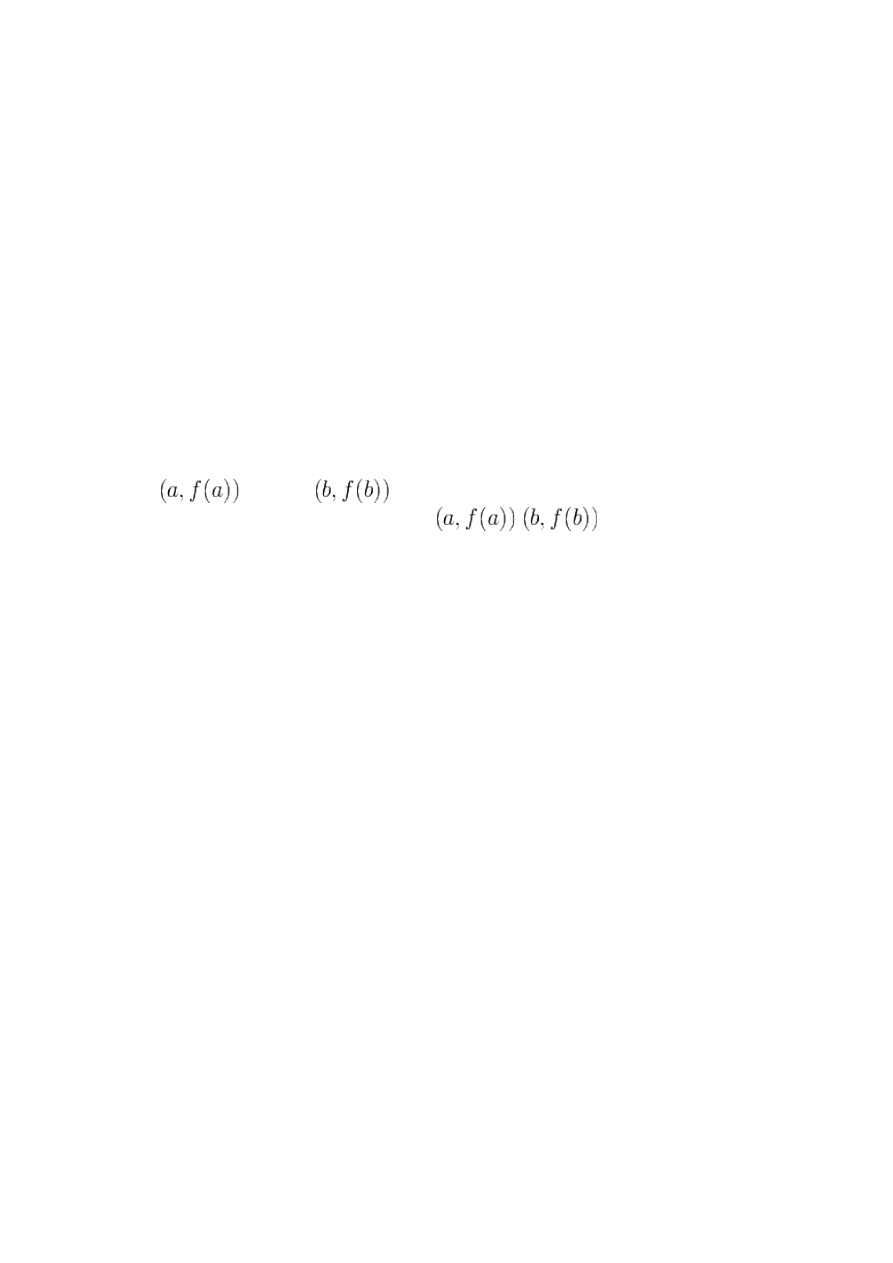
Okresowość
Symetria
Asymptoty
Monotoniczność
Ekstrema
Wypukłość
Infleksja

F(-x)= - f(x) f. nieparzysta (np. sinx)
F(-x)= f(x) f. parzysta (np. cosx)

Tw. Lagrange’a o wartości średniej w funkcji różniczkowalnej.
Jeżeli w przedziale <a;b> funkcja jest różniczkowalna to istnieje w tym przedziale taki punkt
K, że

F(b)-f(a)=f’(K)*f(b-a)

Geometrycznie twierdzenie Lagrange'a oznacza, że na łuku będącym wykresem funkcji od
punktu

do punktu

, istnieje taki punkt, w którym styczna jest równoległa

do siecznej poprowadzonej między punktami

i

.

Tw. Rolle
Szczególny przypadek tw. Lagrange’a
Mówi, że funkcja różniczkowalna, która przyjmuje równe wartości w dwóch punktach musi
mieć punkt, gdzie nachylenie prostej stycznej do wykresu funkcji jest równe zeru.

j. F(a)=f(b) to f’(K)=0

Tw. Taylora

Gdzie R

n+1

= jest to reszta we wzorze Taylora

Szereg Taylora

Gdy a=0 to jest to wzór Maclaurena: