dr hab. Antoni C. Mituś, prof. PWr

Wrocław, 18.10.2012

Fizyka I

Lista 6 - Elementy dynamiki

(zadania oznaczone (!) - w pierwszej kolejności; (*) - nadobowi

,

azkowe)

1. (!) Tematy do dyskusji

(a) Do obu końców dynamometru leż

,

acego na płaskim stole przyczepiono ci

,

eżarki o jed-

nakowych masach m, patrz rys. 1. Jak

,

a sił

,

e wskaże dynamometr?

(b) Do kuli wisz

,

acej na nitce doczepiono tak

,

a sam

,

a nitk

,

e (rys. 2). Co si

,

e stanie, gdy do

dolnej nitki przyłożymy odpowiednio duż

,

a sił

,

e (a) powoli i (b) gwałtownie?

(c) Z jakim maksymalnym przyspieszeniem może poruszać si

,

e samochód, jeżeli współ-

czynnik tarcia mi

,

edzy oponami a podłożem wynosi µ?

2. (!) Siła harmoniczna (w jednym wymiarze) spełnia relacj

,

e F = −k x, gdzie k nosi nazw

,

e

stałej spr

,

eżystości, a x oznacza wychylenie z położenia równowagi.

(a) Wyznaczyć stał

,

a spr

,

eżystości k

z

pojedynczej spr

,

eżyny, równoważnej dwóm spr

,

eżynom

o stałych k

1

, k

2

poł

,

aczonych (i) szeregowo i (ii) równolegle. Równoważność oznacza,

że przyłożona siła powoduje takie samo wychylenie.

(b) Punkt materialny jest przymocowany do dwóch jednakowych spr

,

eżyn, rys. 3.

(a) Czy siła wywołana wychyleniem wzdłuż kierunku (1) jest harmoniczna?
(b) (*) A wzdłuż kierunku (2)?

3. (!) Wyznaczyć wektor siły działaj

,

acej na astronaut

,

e o masie 80 kg znajduj

,

acego si

,

e w

polu grawitacyjnym Ziemi i Ksi

,

eżyca, w odległości 10

5

km od środka Ksi

,

eżyca, rys. 4.

Odległość Ziemia - Ksi

,

eżyc przyj

,

ać w przybliżeniu 3 × 10

5

km. Masa Ziemi: 6 × 10

24

kg,

Ksi

,

eżyca: 7.35 × 10

22

kg.

4. (!) Cz

,

astka o masie m = 3 porusza si

,

e w polu siły ~

F zależnej od czasu t: ~

F = [15 t, 3 t −

12, −6 t

2

]. W chwili pocz

,

atkowej cz

,

astka znajdowała si

,

e w punkcie o współrz

,

ednych

(5, 2, −3) i miała pr

,

edkość v

0

= [2, 0, 1]. Prosz

,

e znaleźć zależność wybranej składowej

pr

,

edkości i położenia cz

,

astki od czasu.

5. (!) Na linie przerzuconej przez blok nieruchomy i przyczepionej do ci

,

eżarka o masie m

znajduje si

,

e małpa o masie M (rys. 5). Z jakim przyspieszeniem a b

,

edzie poruszać si

,

e

ci

,

eżarek

(a) gdy małpa nie porusza si

,

e wzgl

,

edem liny;

(b) gdy małpa wspina si

,

e po linie ze stał

,

a pr

,

edkości

,

a wzgl

,

edem liny;

(c) małpa wspina si

,

e po linie ze stałym przyspieszeniem wzgl

,

edem liny.

Lina porusza si

,

e po bloku bez tarcia.

6. (!) Z jakim minimalnym przyspieszeniem powinien poruszać si

,

e klocek A (rys. 6) aby

masy m

1

i m

2

pozostały w spoczynku wzgl

,

edem niego? Współczynnik tarcia µ mi

,

edzy

masami a klockiem wynosi 0.2, m

1

= 3 kg, m

2

= 5 kg. Mas

,

e kr

,

ażka i nici prosz

,

e zaniedbać.

7. (

∗

) Pokazać, że prawa Newtona nie zmieniaj

,

a swej postaci przy obrotach układu współrz

,

ed-

nych (Feynman, t.1, 11-3).

8. (

∗

) Siła działaj

,

aca na punkt materialny o masie m = 1, poruszaj

,

acy si

,

e po linii prostej,

wynosi F = −x. Znaleźć numerycznie (za pomoc

,

a komputera albo kalkulatora) zależ-

ności x(t), v(t), jeżeli x(0) = 0, v(0) = 1. (Wskazówka: zastosować schemat rozwi

,

azania

omówiony na wykładzie).

9. (

∗∗

) Niech w ruchu jednowymiarowym F (v) = −v oraz v(0) = 1. Znaleźć wyrażenie na

v(t

n

), gdzie t

n

= n ∆t. Wykonać przejście graniczne ∆t → 0, korzystaj

,

ac z zależności

ln(1 + x) ' x dla |x| << 1. Wynik ma postać: v(t) = e

−t

(porównaj zad. 3, lista 3).

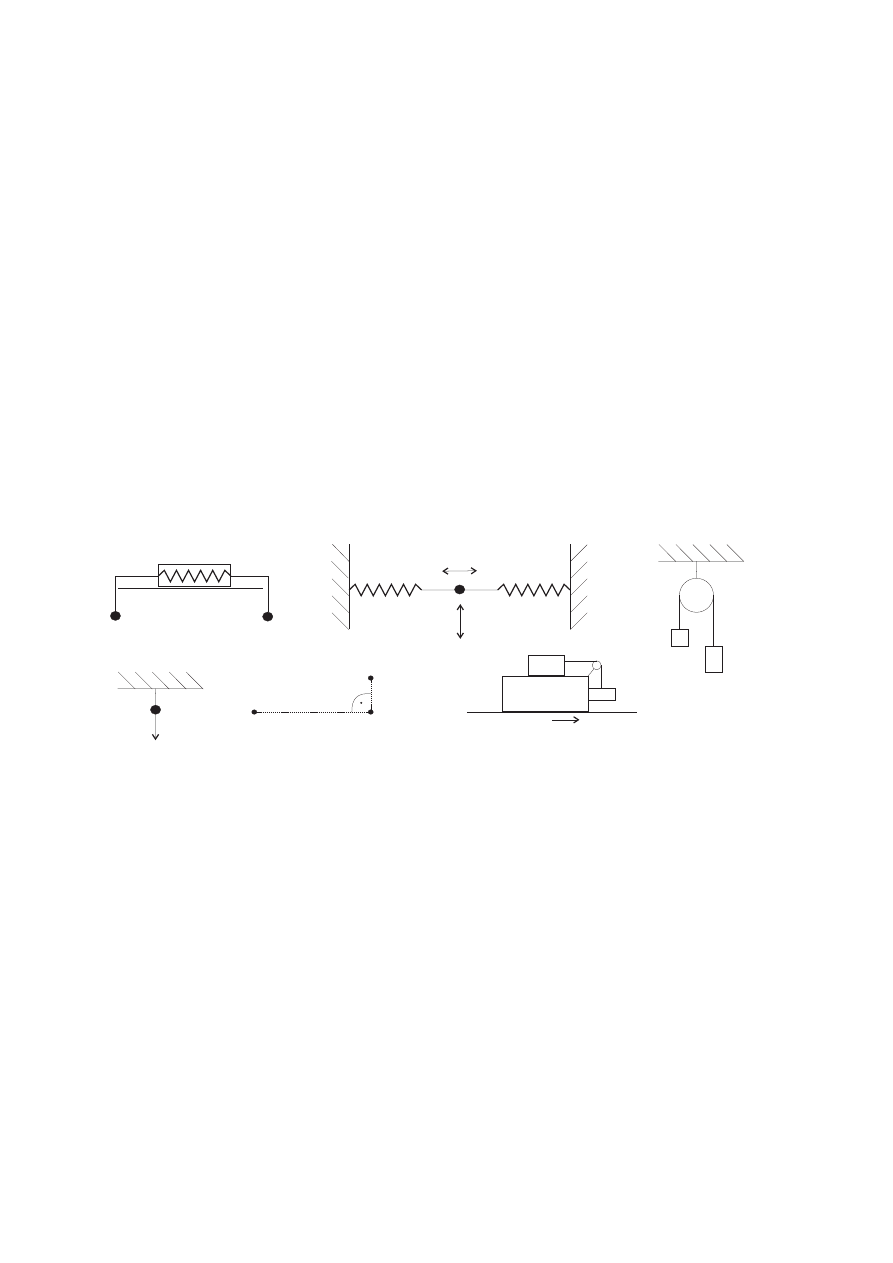
m

m

M

m

(1)

(2)

A

m

1

a

0

m

2

F

astr.

K

Z

Rys. 1

Rys. 6

Rys. 5

Rys. 4

Rys. 2

Rys. 3