dr hab. Antoni C. Mituś, prof. PWr

Wrocław, 03.12.2012

Fizyka I

Lista 9 - Układ wielu punktów/środek masy.

(zadania oznaczone (!) - w pierwszej kolejności; (*) - nadobowi

,

azkowe)

1. (!) Prosz

,

e wyznaczyć położenia środka masy nast

,

epuj

,

acych obiektów (jeżeli nie podano

inaczej, to g

,

estość masy przyj

,

ać za stał

,

a): (a) punktów materialnych o współrz

,

ednych

(0, 0), (0, 1), (2, 0), maj

,

acych jednakowe masy; (b) prostok

,

ata; (c) koła w którym wydr

,

ażono

mniejsze koło; (d)(*) trójk

,

ata równobocznego; (e)(*) połówki koła; (f) (*) obszaru mi

,

edzy

osi

,

a x a wykresem funkcji sin(x) dla 0 ≤ x ≤ π; (g) pr

,

eta, którego g

,

estość masy dana

jest wyrażeniem ρ(x) = α x

2

, gdzie x oznacza odległość od jednego z końców pr

,

eta a α to

stała (w jakich jednostkach jest ona mierzona?); (h) (*) półokr

,

egu.

2. (!) Dwa punkty materialne o jednakowych masach, znajduj

,

ace si

,

e w polu grawitacyjnym

Ziemi na wysokości H, rzucono z jednakowymi pr

,

edkościami v

0

, jeden pionowo do góry,

drugi – pionowo w dół. Wyznaczyć położenie środka masy układu na podstawie:
(a) definicji;
(b) drugiej zasady dynamiki dla ruchu środka masy.
(c) Jakim ruchem (podać równania) poruszaj

,

a si

,

e te punkty w układzie środka masy?

3. (!) Na końcu nieruchomej łódki, znajduj

,

acej si

,

e w wodzie, stoi człowiek. Na jak

,

a odległość

przesunie si

,

e łódka, jeżeli człowiek przejdzie na jej drugi koniec? Ci

,

eżar człowieka wynosi

G, ci

,

eżar łódki P , a jej długość l. Opór wody pomijamy.

4. (!) Do wózka o masie m

1

przyczepiono (w jego środku masy) nieważki pr

,

et o długości L,

na końcu którego umocowano mał

,

a kulk

,

e o masie m

2

. Ruch obrotowy pr

,

eta jest opisany

równaniem φ = φ

0

sin t, (t ≥ 0) (rys. 2). Prosz

,

e zaniedbać tarcie i przyj

,

ać, że przed

rozpocz

,

eciem ruchu pr

,

eta (t < 0) wózek był w spoczynku.

(a) Znaleźć równanie ruchu wózka (położenie jego środka). (Układ odosobniony, środek
masy).
(b) (*) Korzystaj

,

ac z równania Newtona dla ruchu środka masy, znaleźć nacisk wózka na

poziom

,

a płaszczyzn

,

e.

5. (!) Dwa punkty materialne o masach m

1

, m

2

poruszaj

,

ace si

,

e wzdłuż linii prostej poł

,

aczono

spr

,

eżyn

,

a o długości l

0

. Do rozci

,

agni

,

ecia spr

,

eżyny do długości l potrzebna jest siła

F = −k(l − l

0

) (k > 0). Spr

,

eżyn

,

e rozci

,

agni

,

eto a nast

,

epnie zwolniono. Prosz

,

e napi-

sać równanie ruchu (Newtona) opisuj

,

ace zależność od czasu wzgl

,

ednej odległości mi

,

edzy

punktami materialnymi. Co si

,

e dzieje w przypadku, gdy m

1

<< m

2

? (Zagadnienie dwóch

ciał).

6. Samochód porusza si

,

e z pr

,

edkości

,

a v.

(a) (!) Wyznaczyć wektory pr

,

edkości cz

,

astek opony samochodu w punktach A, B, C, D

(rys. 3). Kierunek OD tworzy k

,

at π/4 z osi

,

a poziom

,

a.

(b) (*) Powyższe zadanie dla dowolnego punktu na oponie.
(c) Napisać równanie toru (w postaci parametrycznej, tj., x = x(t), y = y(t)) po którym
porusza si

,

e punkt materialny odległy o r od środka opony. (Wskazówka: składanie ruchów,

układ środka masy)

7. (!) Obr

,

ecz o masie m stacza si

,

e z równi pochyłej o wysokości h i k

,

acie nachylenia α.

(a) Obliczyć pr

,

edkość obr

,

eczy po stoczeniu si

,

e do poziomu ziemi. (Wskazówka: prawo

zachowania energii, energia kinetyczna w środku masy)
(b) Obliczyć przyspieszenie, z jakim porusza si

,

e obr

,

ecz. (Wskazówka: ruch jednostajnie

przyspieszony)
(c) Jak zmieni

,

a si

,

e wyniki, gdy stacza si

,

e cienki wydr

,

ażony walec (rura)?

(d) (*) Jak zmieni

,

a si

,

e wyniki, gdy stacza si

,

e pełny walec?

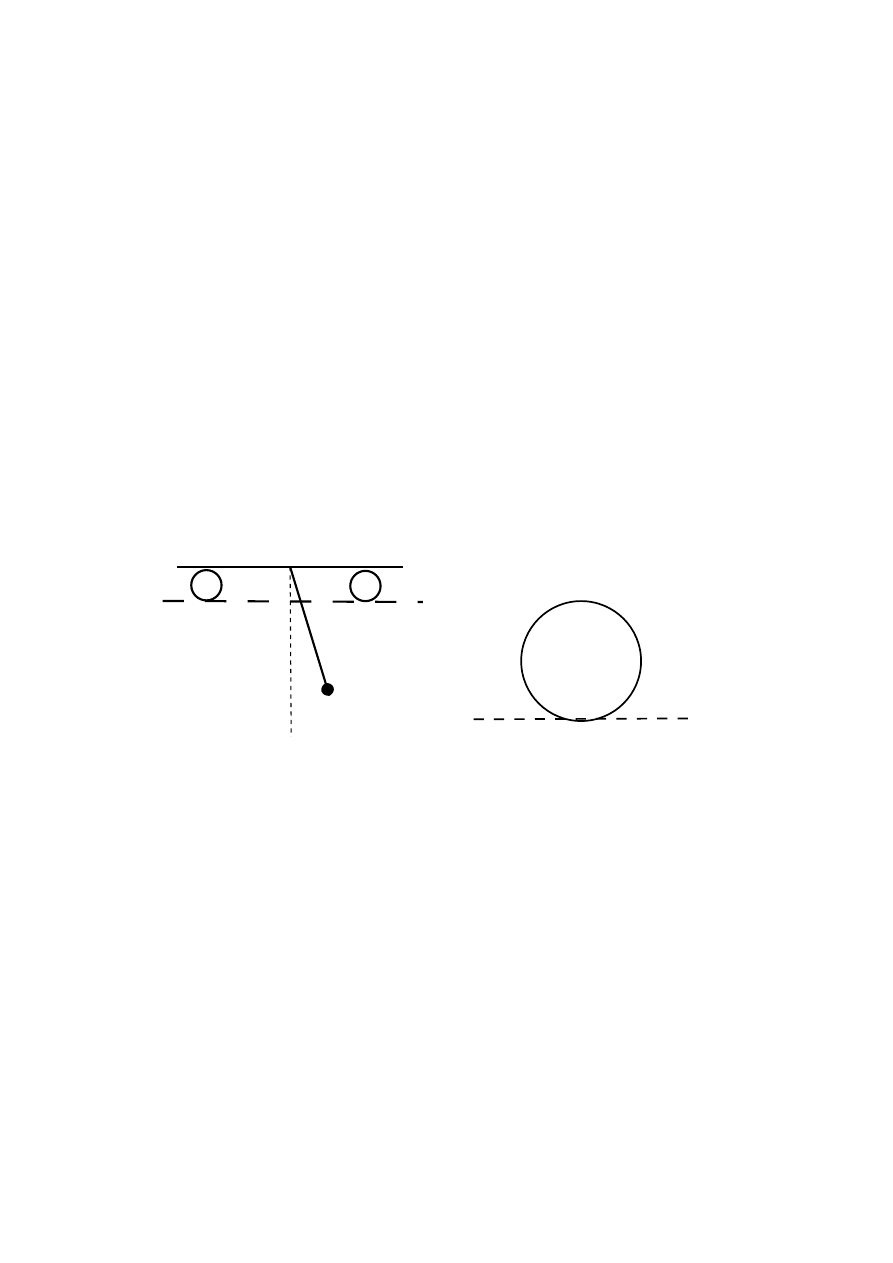
C M

m 2

p h i

L

r y s . 2

A

B

C

D

r y s . 3

O