1

1

Materiały dydaktyczne zawieraj

ą

ce 23 slajdy na 12 stronach,

dotycz

ą

ce

ć

wiczenia T9 z przedmiotu „Wytrzymało

ść

materiałów”,

przeznaczone

dla studentów II roku studiów I stopnia w kierunku „Energetyka”

na wydz. Energetyki i Paliw w AGH

Autor materiałów i osoba prowadz

ą

ca

ć

wiczenia:

Marek Płachno, dr hab. in

ż

., prof. AGH

Autor nie wyra

ż

a zgody na inne wykorzystywanie tych materiałów,

ni

ż

podane w ich przeznaczeniu.

Ć

wiczenie T9 – cz

ęść

1

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych i

rozci

ą

ganych

Przykład nr 1 –

Temat

=

J

o

k

2

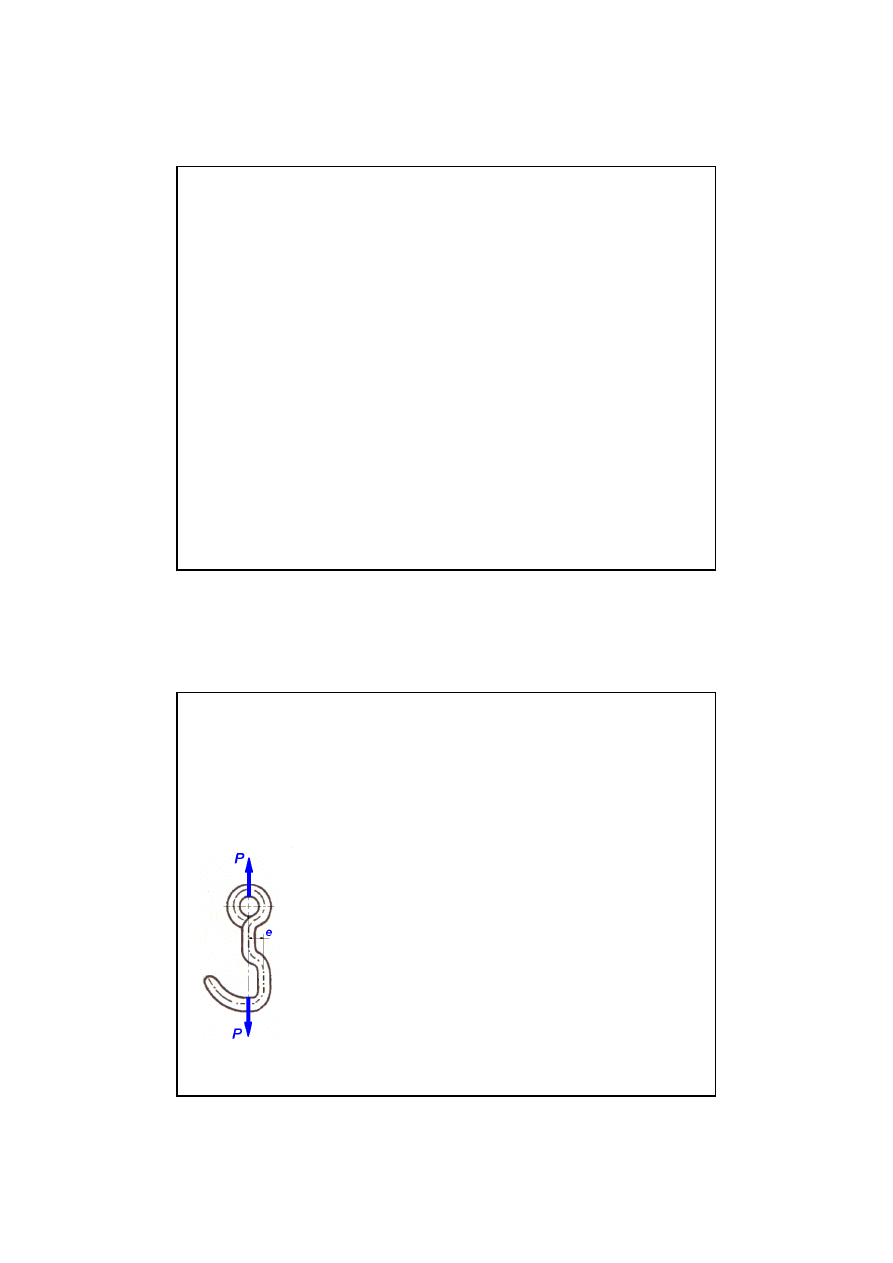
Na haku, pokazanym na rysunku, ma by

ć

zawieszony pojemnik z ładunkiem o całkowitej masie

m = 3,6 Mg. Sprawdzi

ć

warunek

bezpiecze

ń

stwa

haka, je

ż

eli jest on wykonany z rury o

ś

red -

nicach D = 50 mm, d = 40 mm, ma napr

ęż

enia dopuszczalne k

g

= k

r

= 250 MPa oraz ma

wymiar e = 50 mm.

Cztery

kroki

obliczeniowe

1. Dobór i zestawienie

wzorów

do oblicze

ń

.

2. Tablica

danych

oraz szablon tablicy

wyników

oblicze

ń

.

3. Obliczenia i wypełnianie tablicy

wyników

oblicze

ń

.

4. Sformułowanie

liczbowej

postaci warunku

bezpiecze

ń

stwa

oraz

wniosku

do uzyskanych wyników.

2

3

Ć

wiczenie T9 -

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych i

rozci

ą

ganych

, zginanych i

ś

ciskanych

oraz zginanych i

skr

ę

canych

Na

ć

wiczeniuT9 -, studenci poznaj

ą

praktyczne podej

ś

cie do analizy

wytrzymało

ś

ciowej pr

ę

tów obci

ąż

onych

równocze

ś

nie

wi

ę

cej ni

ż

jednym

rodzajem

obci

ąż

enia wewn

ę

trznego

Pr

ę

ty

równocze

ś

nie

zginane i

rozci

ą

gane

maj

ą

przekroje obci

ąż

one

równocze

ś

nie

przez moment wewn

ę

trz -

ny zginaj

ą

cy oraz przez sił

ę

wewn

ę

trzn

ą

wzdłu

ż

n

ą

dodatni

ą

.

►

Pr

ę

ty

równocze

ś

nie

zginane i

ś

ciskane

maj

ą

przekroje obci

ąż

one

równocze

ś

nie

przez moment wewn

ę

trz -

ny zginaj

ą

cy oraz przez sił

ę

wewn

ę

trzn

ą

wzdłu

ż

n

ą

ujemn

ą

.

►

Pr

ę

ty

równocze

ś

nie

zginane i

skr

ę

cane

►

maj

ą

przekroje obci

ąż

one

równocze

ś

nie

przez moment wewn

ę

trz -

ny zginaj

ą

cy oraz przez moment wewn

ę

trzny

skr

ę

caj

ą

cy

.

Ć

wiczenie T9 – cz

ęść

1

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych i

rozci

ą

ganych

Przykład nr 1 –

Temat

=

J

o

k

4

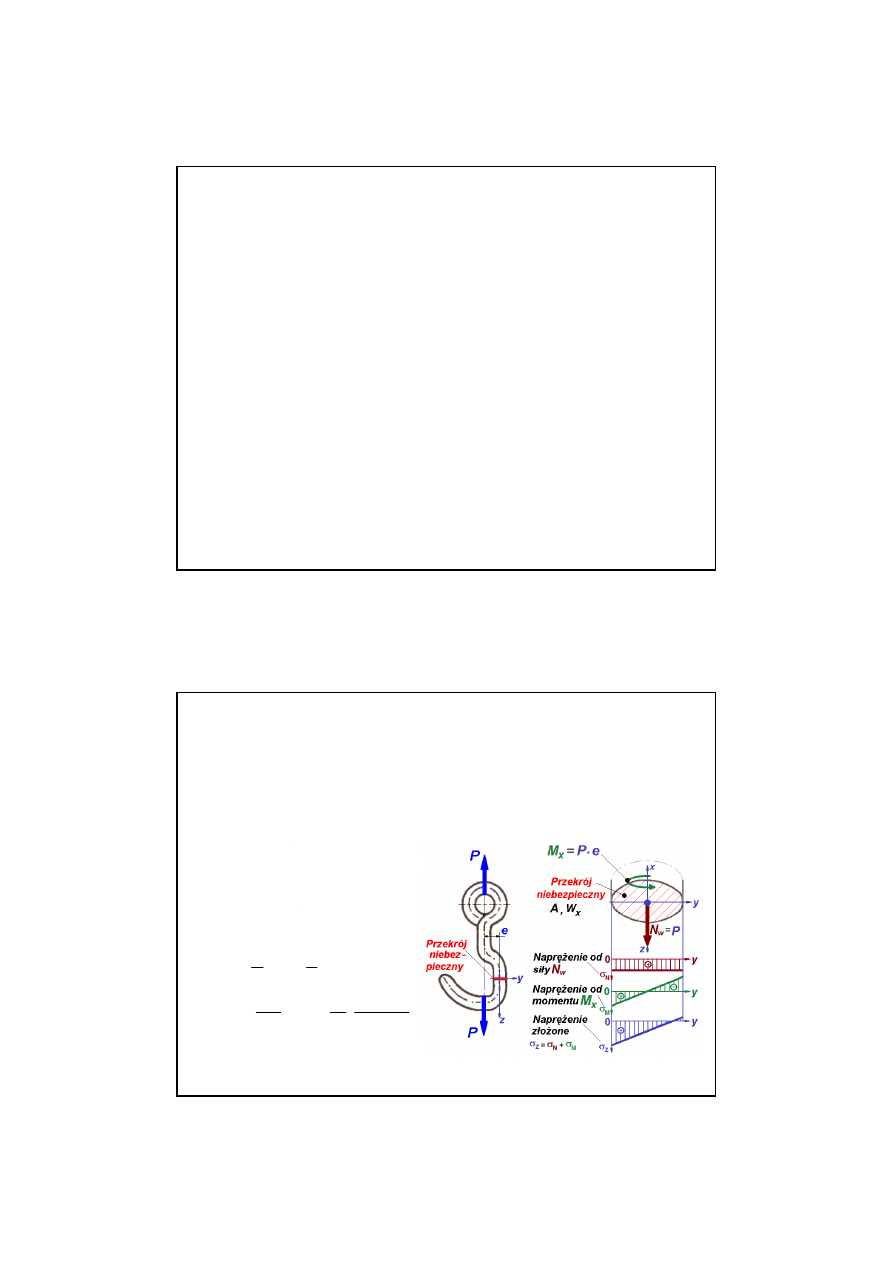
Na haku ma by

ć

zawieszony pojemnik z ładunkiem o całkowitej masie m = 3,6 Mg. Sprawdzi

ć

warunek

bezpiecze

ń

stwa

haka, je

ż

eli odległo

ść

e = 50 mm, a wykonano go z rury o

ś

redni -

cach D = 50 mm, d = 40 mm maj

ą

cej napr

ęż

enia dopuszczalne k

c

= k

r

= 250 MPa.

Krok 1 - dobór i zestawienie

wzorów

do oblicze

ń

.

D

)

d

D

(

32

W

,

W

P

e

)

d

D

(

4

A

,

A

P

k

,

g

m

P

4

4

x

x

max

M

2

2

max

N

max

M

max

N

max

z

r

max

z

−−−−

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

−−−−

⋅⋅⋅⋅

====

====

++++

====

≤≤≤≤

⋅⋅⋅⋅

====

ππππ

σσσσ

ππππ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

3

Ć

wiczenie T9 – cz

ęść

1

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych i

rozci

ą

ganych

Przykład nr 1 –

Temat

=

J

o

k

5

Na haku ma by

ć

zawieszony pojemnik z ładunkiem o całkowitej masie m = 3,6 Mg. Sprawdzi

ć

warunek

bezpiecze

ń

stwa

haka, je

ż

eli odległo

ść

e = 50 mm, a wykonano go z rury o

ś

redni -

cach D = 50 mm, d = 40 mm maj

ą

cej napr

ęż

enia dopuszczalne k

c

= k

r

= 250 MPa.

Krok 2 - Tablica

danych

oraz szablon tablicy

wyników

oblicze

ń

D

)

d

D

(

32

W

,

W

P

e

,

)

d

D

(

4

A

,

A

P

,

,

k

,

g

m

P

4

4

x

x

max

M

2

2

max

N

max

M

max

N

max

z

r

max

z

−−−−

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

−−−−

⋅⋅⋅⋅

====

====

++++

====

≤≤≤≤

⋅⋅⋅⋅

====

ππππ

σσσσ

ππππ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

3,6

250

9,81

50

40

50

Mg

MPa

m/s

2

mm

mm

mm

m

k

r

g

e

d

D

?

MPa

σσσσ

zmax

?

?

?

?

?

MPa

MPa

cm

3

kN

cm

2

σσσσ

Mmax

σσσσ

Nmax

W

X

P

A

Ć

wiczenie T9 – cz

ęść

1

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych i

rozci

ą

ganych

Przykład nr 1 –

Temat

=

J

o

k

6

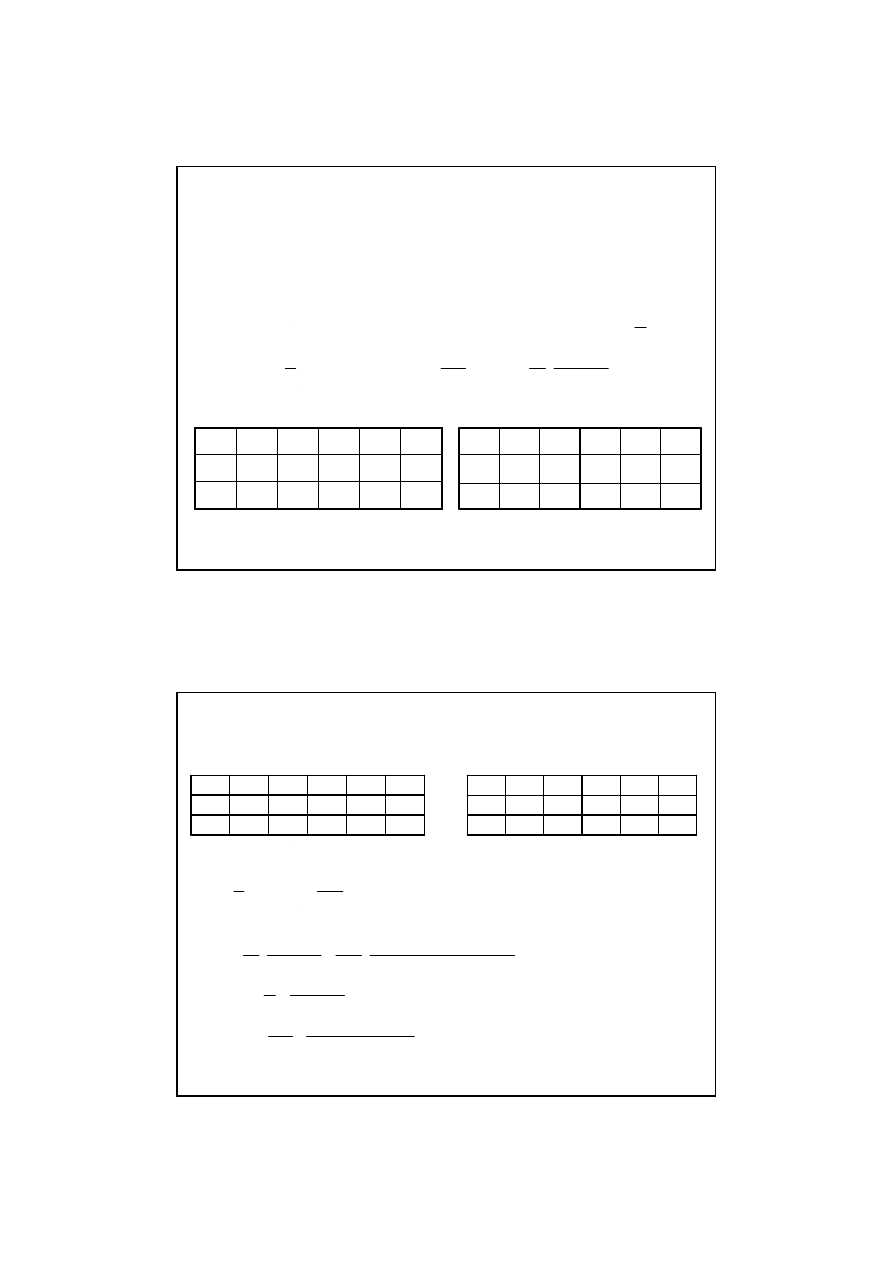
Krok 3 - obliczenia i wypełnianie tablicy

wyników

oblicze

ń

294,8

MPa

σσσσ

zmax

245,1

49,7

7,2

35,3

7,1

MPa

MPa

cm

3

kN

cm

2

σσσσ

Mmax

σσσσ

Nmax

W

X

P

A

[[[[

]]]]

[[[[

]]]]

MPa

294,8

MPa

1

,

245

MPa

49,7

MPa

1

,

245

Pa

10

14

,

245

10

2

,

7

10

3

,

35

10

0

5

W

P

e

MPa

49,7

Pa

10

49,72

10

1

,

7

10

3

,

35

A

P

cm

2

,

7

m

10

24

,

7

10

50

)

10

40

(

)

10

50

(

32

14

,

3

D

)

d

D

(

32

W

,

kN

35,3

N

10

32

,

35

81

,

9

10

3,6

g

m

P

cm

1

,

7

m

10

07

,

7

)

10

40

(

)

10

50

(

4

14

,

3

)

d

D

(

4

A

max

M

max

N

max

z

6

6

3

3

-

x

max

M

6

4

3

max

N

3

3

6

3

-

4

3

-

4

3

-

4

4

x

3

3

2

2

4

2

3

-

2

3

-

2

2

====

++++

====

++++

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

⋅⋅⋅⋅

====

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

⋅⋅⋅⋅

====

−−−−

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

⋅⋅⋅⋅

====

−−−−

⋅⋅⋅⋅

====

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

ππππ

ππππ

−−−−

−−−−

−−−−

−−−−

3,6

250

9,81

50

40

50

Mg

MPa

m/s

2

mm

mm

mm

m

k

r

g

e

d

D

Tablica danych

Tablica

wyników

oblicze

ń

4

Ć

wiczenie T9 – cz

ęść

1

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych i

rozci

ą

ganych

Przykład nr 1 –

Temat

=

J

o

k

7

Na haku, pokazanym na rysunku, ma by

ć

zawieszony pojemnik z ładunkiem o całkowitej masie

m = 3,6 Mg. Sprawdzi

ć

warunek

bezpiecze

ń

stwa

haka, je

ż

eli jest on wykonany z rury o

ś

red -

nicach D = 50 mm, d = 40 mm, ma napr

ęż

enia dopuszczalne k

g

= k

r

= 250 MPa oraz ma

wymiar e = 50 mm.

Tablica wyników oblicze

ń

294,8

245,1

49,7

7,2

35,3

7,1

MPa

MPa

MPa

cm

3

kN

cm

2

σσσσ

zmax

σσσσ

Mmax

σσσσ

Nma

x

W

X

P

A

Krok 4 - Sformułowanie

liczbowej

postaci warunku

bezpiecze

ń

stwa

oraz

wniosku

do uzyskanych

wyników

MPa

250

k

MPa

8

,

294

1

,

245

7

,

49

r

max

M

max

N

max

z

====

>>>>

====

++++

====

++++

====

σσσσ

σσσσ

σσσσ

Dla zadanego obci

ąż

enia, warunek

bezpiecze

ń

stwa

haka

nie

jest

spełniony.

Wniosek

Gdyby przy sprawdzaniu warunku

bezpiecze

ń

stwa

haka pomini

ę

to jego sił

ę

wewn

ę

trzn

ą

rozci

ą

gaj

ą

c

ą

, to uzyskany wtedy pozytywny

wynik

sprawdzenia byłby

niezgodny

z faktycznym

bezpiecze

ń

stwem

tego haka.

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych i

skr

ę

canych

Przykład nr 2 –

Temat

=

J

o

k

8

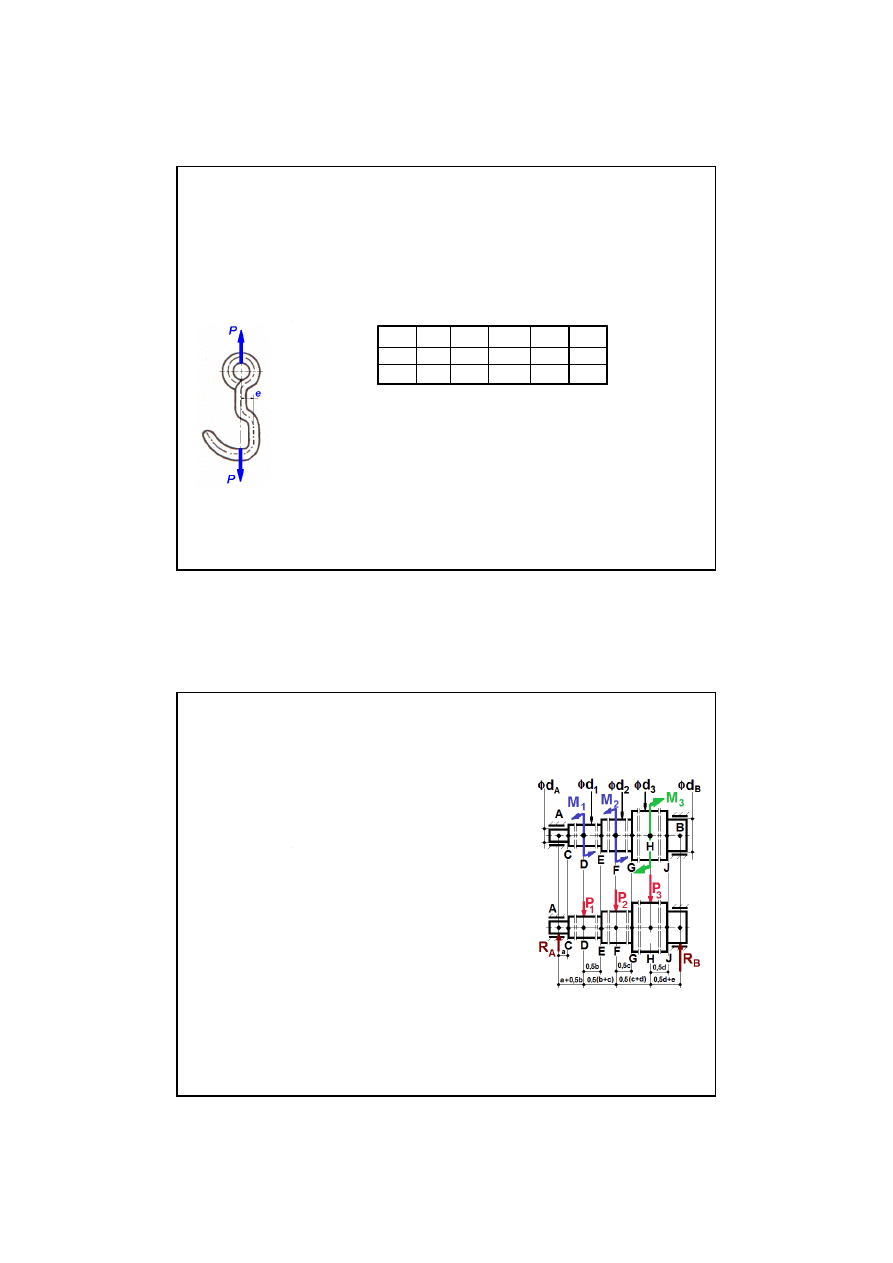
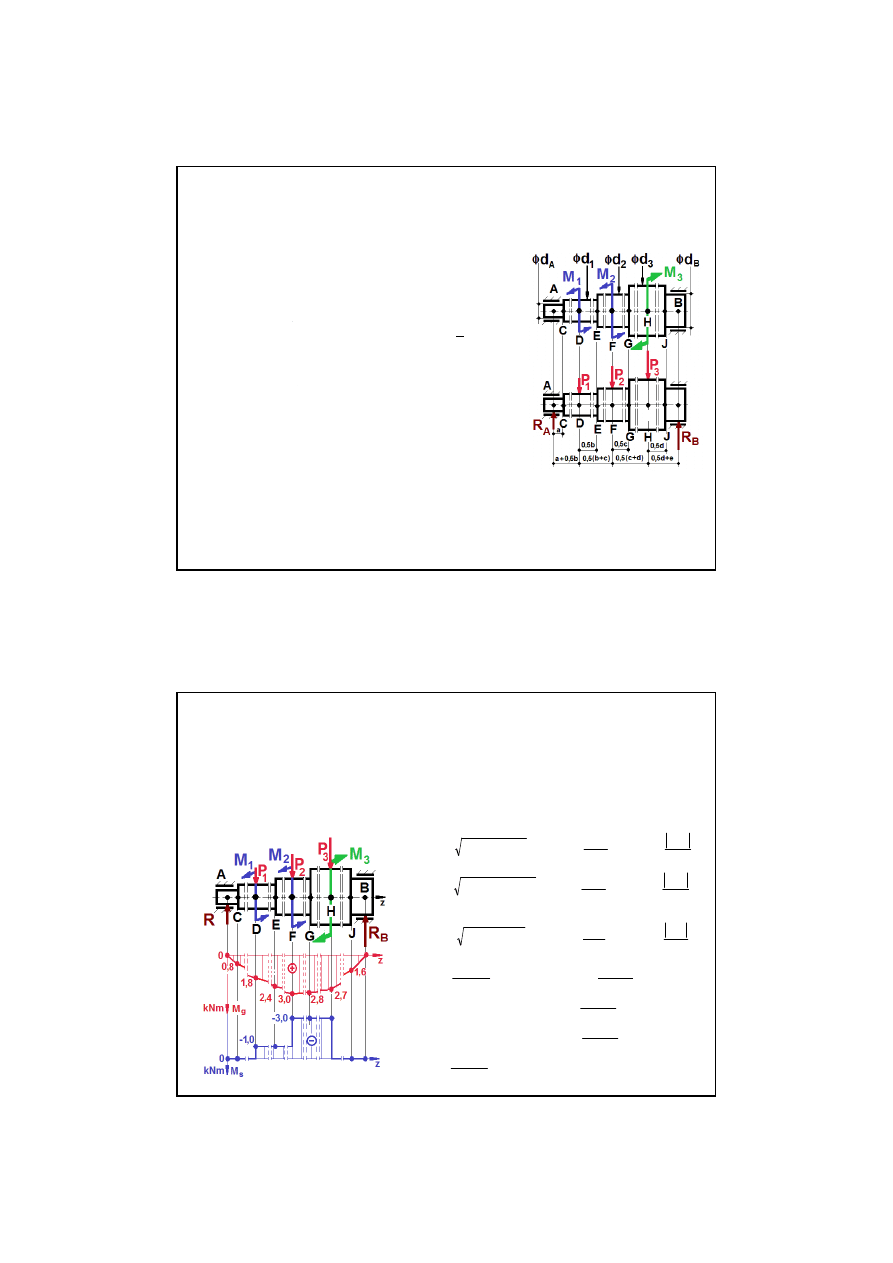
Sprawdzi

ć

warunek

bezpiecze

ń

stwa

wału obci

ąż

onego

rów-

nocze

ś

nie

momentami obrotowymi

M

1

,

M

2

i

M

3

oraz czyn -

nymi siłami skupionymi

P

1

,

P

2

i

P

3

- jak na rysunku, je

ż

eli:

a = 0,2 m, b = 0,6 m, c = 0,5 m, d = 0,4 m, e = 0,3 m, d

A

=

40 mm, d

1

= 50 mm, d

2

= 65 mm, d

3

= 100 mm, d

B

= 65 mm,

k

r

= 200 MPa, M

1

= 1 kNm, M

2

= 2 kNm, M

3

= 3 kNm, P

1

=1,5

kN, P

2

= 3,0 kN, P

3

= 4,5 kN.

Nowe

poj

ę

cia do

samodzielnego

opanowania

1. Definicja i miara fizyczna wyt

ęż

enia materiału.

2. Zało

ż

enia, zakres przydatno

ś

ci i podstawowe wzory algeb -

raiczne dotycz

ą

ce aktualnie stosowanych

hipotez

wyt

ę

-

ż

eniowych.

3. Warunek

bezpiecze

ń

stwa

dla

równoczesnego

zginania

i

skr

ę

cania

wynikaj

ą

cy z

hipotezy

energii wła

ś

ciwej postaciowego odkształcenia materiału

spr

ęż

ysto - plastycznego.

4. Warunek

bezpiecze

ń

stwa

dla

równoczesnego

zginania i

skr

ę

cania

wynikaj

ą

cy z

hipotezy

najwi

ę

kszego

wydłu

ż

enia

jednostkowego

w materiale spr

ęż

ysto - kruchym.

5

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych i

skr

ę

canych

Przykład nr 2 –

Temat

=

J

o

k

9

Sprawdzi

ć

warunek

bezpiecze

ń

stwa

wału obci

ąż

onego

rów-

nocze

ś

nie

momentami obrotowymi

M

1

,

M

2

i

M

3

oraz czyn -

nymi siłami skupionymi

P

1

,

P

2

i

P

3

- jak na rysunku, je

ż

eli:

a = 0,2 m, b = 0,6 m, c = 0,5 m, d = 0,4 m, e = 0,3 m, d

A

=

30 mm, d

1

= 50 mm, d

2

= 65 mm, d

3

= 100 mm,d

B

= 65 mm

k

r

= 200 MPa, M

1

= 1 kNm, M

2

= 2 kNm, M

3

= 3 kNm, P

1

=

= 1,5 kN, P

2

= 3,0 kN, P

3

= 4,5 kN.

Pi

ęć

kroków

obliczeniowych

1.Wykresy

rozkładu

po długo

ś

ci wału momentu wewn

ę

trzne-

go skr

ę

caj

ą

cego i momentu wewn

ę

trznego zginaj

ą

cego.

2. Dobór i zestawienie

wzorów

do oblicze

ń

.

3. Tablica

danych

oraz szablon tablicy

wyników

oblicze

ń

.

4. Obliczenia i wypełnianie tablicy

wyników

oblicze

ń

.

5. Sformułowanie

liczbowej

postaci warunku

bezpiecze

ń

stwa

oraz

wniosku

do uzyskanych

wyników.

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych

i

skr

ę

canych

Przykład nr 2: Sprawdzi

ć

warunek

bezpiecze

ń

stwa

wału obci

ąż

onego

równocze

ś

nie

momen -

tami obrotowymi

M

1

,

M

2

i

M

3

oraz czynnymi siłami skupionymi

P

1

,

P

2

i

P

3

=

J

o

k

10

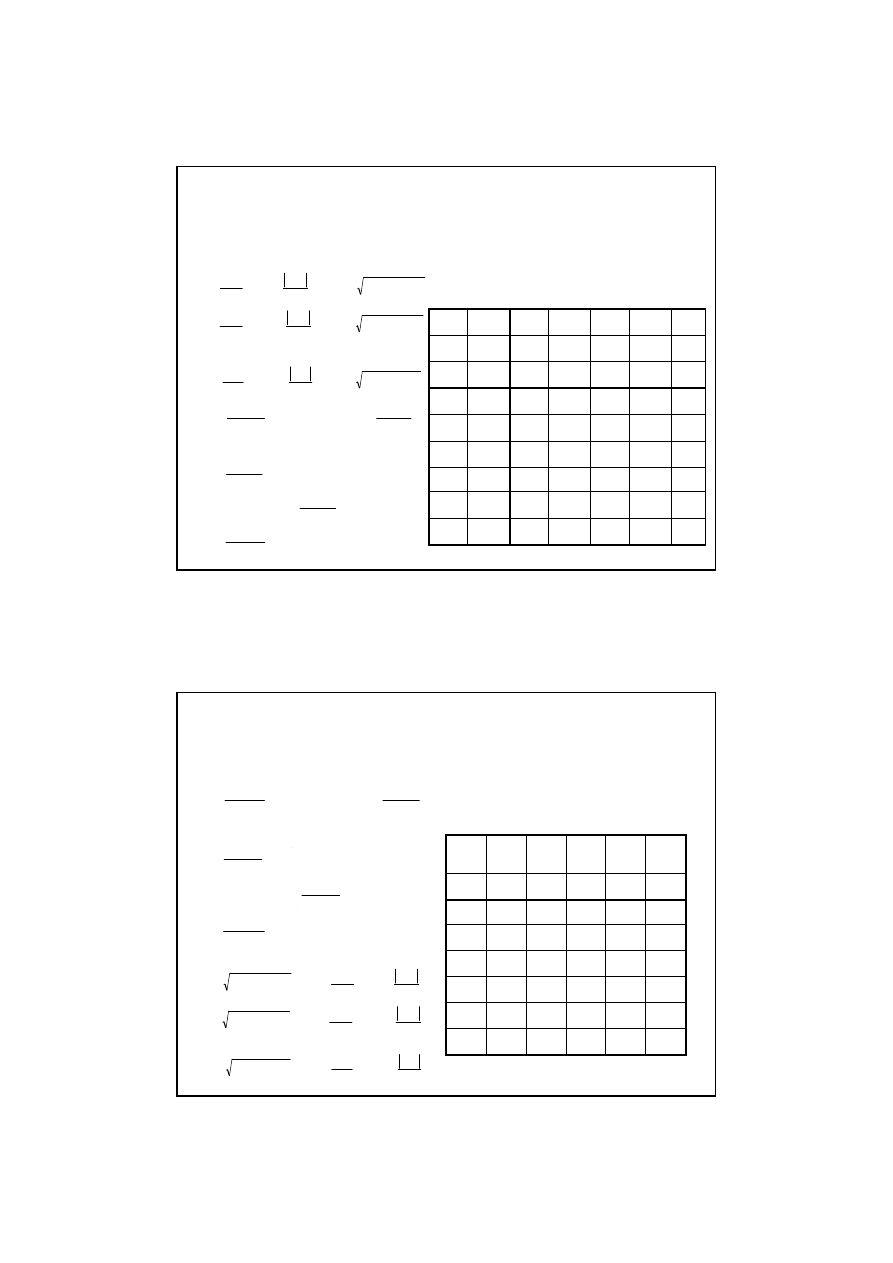
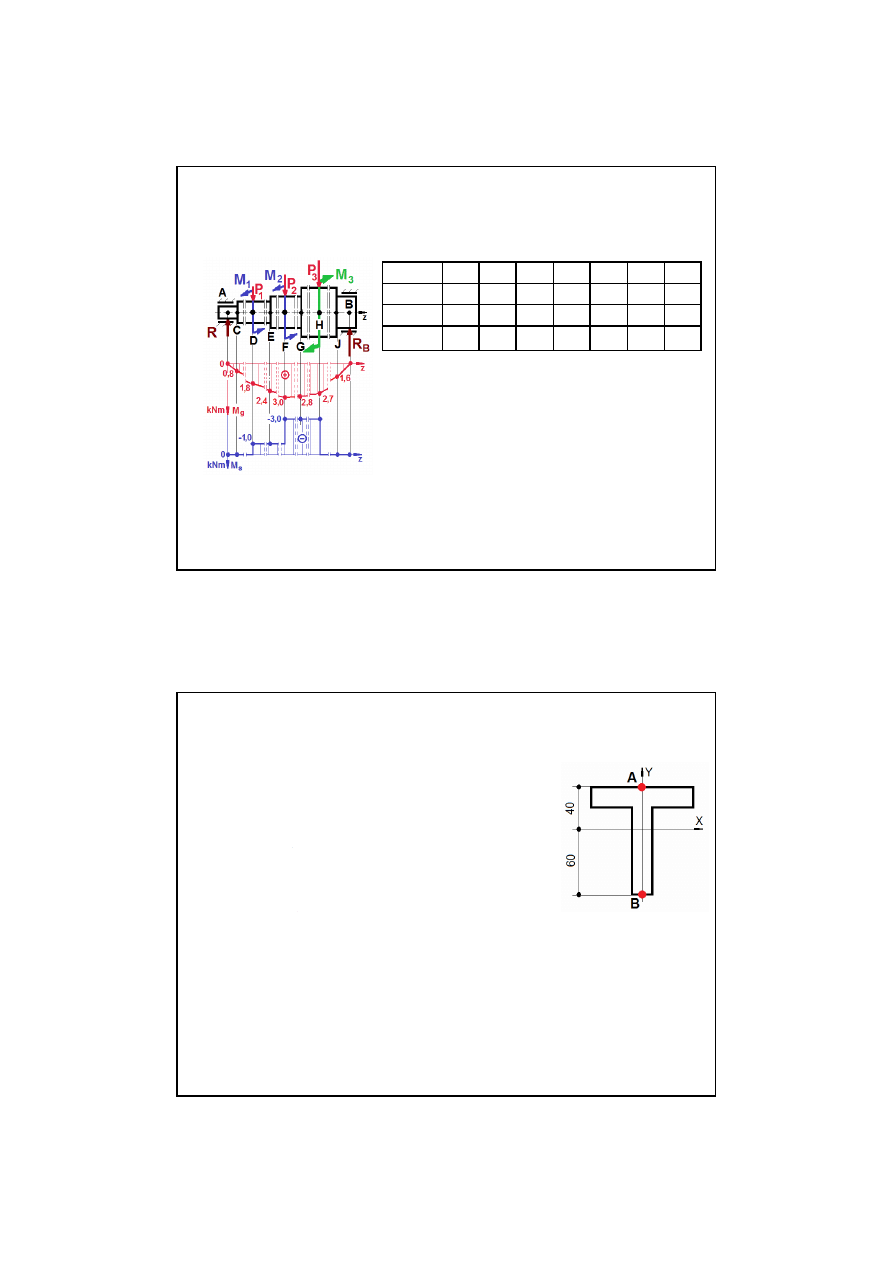
Krok 1 - Wykresy

rozkładu

po dłu -

go

ś

ci wału momentu wewn

ę

trznego

zginaj

ą

cego

i

skr

ę

caj

ą

cego

.

Krok 2 - Dobór i zestawienie

wzorów

do oblicze

ń

.

xJ

oJ

3

B

xJ

xH

oH

3

3

xH

xG

oG

xF

xG

xF

oF

3

2

xF

xE

oE

xD

xE

xD

oD

3

1

xD

xC

oC

3

A

xC

W

2

W

,

32

)

d

(

W

W

2

W

,

32

)

d

(

W

,

W

2

W

,

W

W

W

2

W

,

32

)

d

(

W

,

W

2

W

,

W

W

W

2

W

,

32

)

d

(

W

,

W

2

W

,

32

)

d

(

W

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

ππππ

ππππ

ππππ

ππππ

ππππ

,

oJ

sJ

J

xJ

gJ

J

2

J

2

J

zJ

W

M

W

M

,

3

====

ττττ

====

σσσσ

ττττ

⋅⋅⋅⋅

++++

σσσσ

σσσσ

====

oD

sD

D

xD

gD

D

2

D

2

D

zD

oC

sC

C

xC

gC

C

2

C

2

C

zC

W

M

W

M

,

3

W

M

W

M

,

3

,

,

====

ττττ

====

σσσσ

ττττ

⋅⋅⋅⋅

++++

σσσσ

====

ττττ

====

σσσσ

ττττ

⋅⋅⋅⋅

++++

σσσσ

σσσσ

====

σσσσ

====

……………………………………………

r

zJ

zH

zG

zF

zE

zD

zC

max

z

k

)

,

,

,

,

,

,

max(

≤≤≤≤

====

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

6

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych

i

skr

ę

canych

Przykład nr 2: Sprawdzi

ć

warunek

bezpiecze

ń

stwa

wału obci

ąż

onego

równocze

ś

nie

momen -

tami obrotowymi

M

1

,

M

2

i

M

3

oraz czynnymi siłami skupionymi

P

1

,

P

2

i

P

3

=

J

o

k

11

xJ

oJ

3

B

xJ

xH

oH

3

3

xH

xG

oG

xF

xG

xF

oF

3

2

xF

xE

oE

xD

xE

xD

oD

3

1

xD

xC

oC

3

A

xC

W

2

W

,

32

)

d

(

W

W

2

W

,

32

)

d

(

W

,

W

2

W

,

W

W

,

W

2

W

,

32

)

d

(

W

W

2

W

,

W

W

,

W

2

W

32

)

d

(

W

,

W

2

W

,

32

)

d

(

W

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

ππππ

ππππ

ππππ

ππππ

ππππ

,

,

,

,

2

D

2

D

zD

oD

sD

D

xD

gD

D

2

C

2

C

zC

oC

sC

C

xC

gC

C

3

W

M

W

M

3

W

M

W

M

ττττ

⋅⋅⋅⋅

++++

σσσσ

====

ττττ

====

σσσσ

ττττ

⋅⋅⋅⋅

++++

σσσσ

σσσσ

====

ττττ

====

σσσσ

====

σσσσ

====

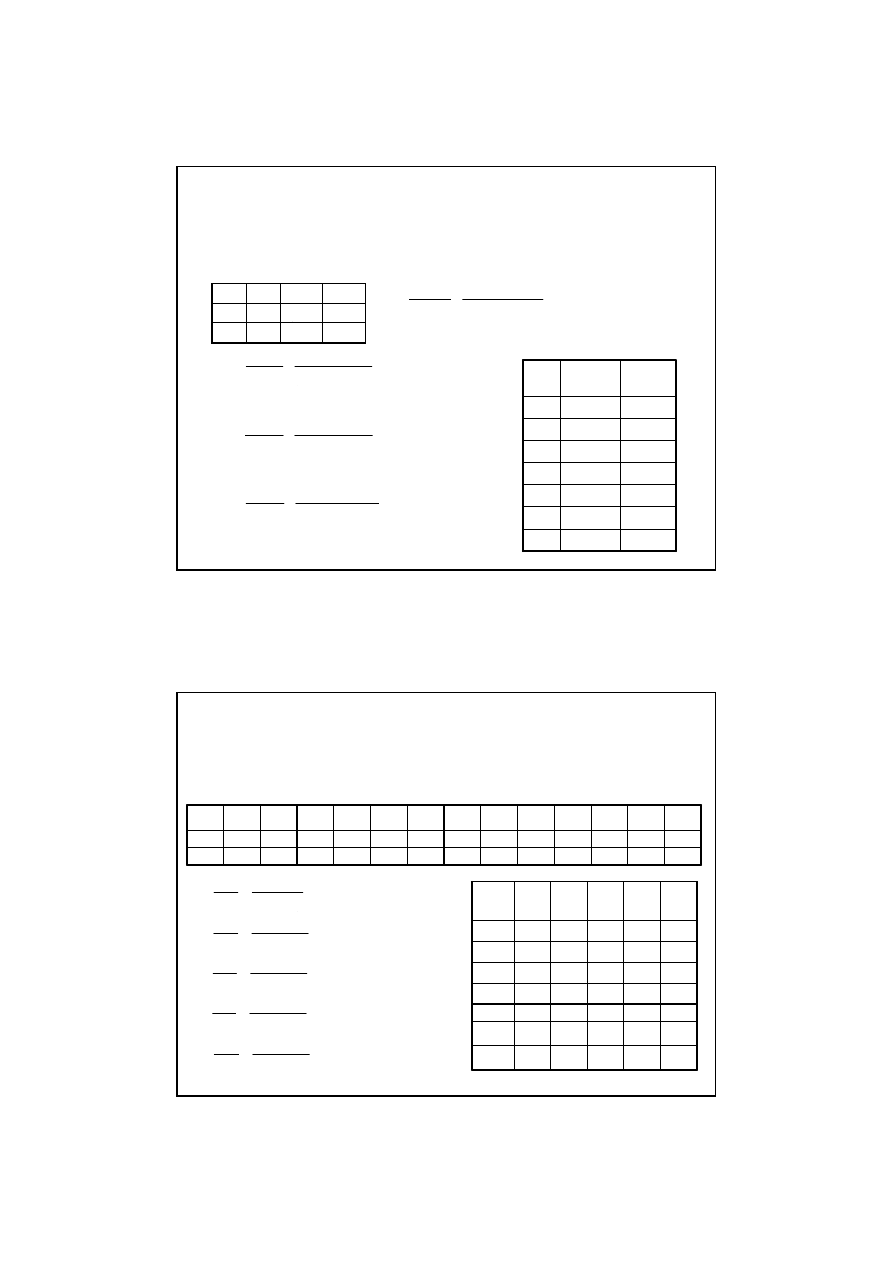
Krok 3 - Tablica

danych

oraz szablon tablicy

wyników

oblicze

ń

– cz.1 - tablica

danych

3

W

M

W

M

2

J

2

J

zJ

oJ

sJ

J

xJ

gJ

J

,

,

ττττ

⋅⋅⋅⋅

++++

σσσσ

σσσσ

====

ττττ

====

σσσσ

====

……………………………………………

200

MPa

k

r

-3

kNm

M

sH

1,6

kNm

M

gJ

65

100

65

50

40

0

mm

mm

mm

mm

mm

kNm

d

B

d

3

d

2

d

1

d

A

M

sJ

0

-3

-3

-1

-1

0

kNm

kNm

kNm

kNm

kNm

kNm

M

sC

M

sG

M

sF

M

sE

M

sD

M

sC

2,7

2,8

3,0

2,4

1,8

0,8

kNm

kNm

kNm

kNm

kNm

kNm

M

g

H

M

gG

M

gF

M

gE

M

gD

M

gC

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych

i

skr

ę

canych

Przykład nr 2: Sprawdzi

ć

warunek

bezpiecze

ń

stwa

wału obci

ąż

onego

równocze

ś

nie

momen -

tami obrotowymi

M

1

,

M

2

i

M

3

oraz czynnymi siłami skupionymi

P

1

,

P

2

i

P

3

=

J

o

k

12

xJ

oJ

3

B

xJ

xH

oH

3

3

xH

xG

oG

xF

xG

xF

oF

3

2

xF

xE

oE

xD

xE

xD

oD

3

1

xD

xC

oC

3

A

xC

W

2

W

,

32

)

d

(

W

W

2

W

,

32

)

d

(

W

,

W

2

W

,

W

W

,

W

2

W

,

32

)

d

(

W

W

2

W

,

W

W

,

W

2

W

32

)

d

(

W

,

W

2

W

,

32

)

d

(

W

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

ππππ

ππππ

ππππ

ππππ

ππππ

,

,

oD

sD

D

xD

gD

D

2

D

2

D

zD

oC

sC

C

xC

gC

C

2

C

2

C

zC

W

M

W

M

,

3

W

M

W

M

,

3

====

ττττ

====

σσσσ

ττττ

⋅⋅⋅⋅

++++

σσσσ

====

ττττ

====

σσσσ

ττττ

⋅⋅⋅⋅

++++

σσσσ

σσσσ

====

σσσσ

====

Krok 3 - Tablica

danych

oraz szablon tablicy

wyników

oblicze

ń

– cz.1 – tablica

wyników

,

oJ

sJ

J

xJ

gJ

J

2

J

2

J

zJ

W

M

W

M

,

3

====

ττττ

====

σσσσ

ττττ

⋅⋅⋅⋅

++++

σσσσ

σσσσ

====

……………………………………………

J

H

G

F

E

D

C

Przek-

rój

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

σσσσ

z

,

MPa

ττττ

,

MPa

σσσσ

,

MPa

W

o

,

cm

3

W

x

,

cm

3

)

,

,

,

,

,

,

max(

zJ

zH

zG

zF

zE

zD

zC

max

z

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

====

7

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych

i

skr

ę

canych

Przykład nr 2: Sprawdzi

ć

warunek

bezpiecze

ń

stwa

wału obci

ąż

onego

równocze

ś

nie

momen -

tami obrotowymi

M

1

,

M

2

i

M

3

oraz czynnymi siłami skupionymi

P

1

,

P

2

i

P

3

=

J

o

k

13

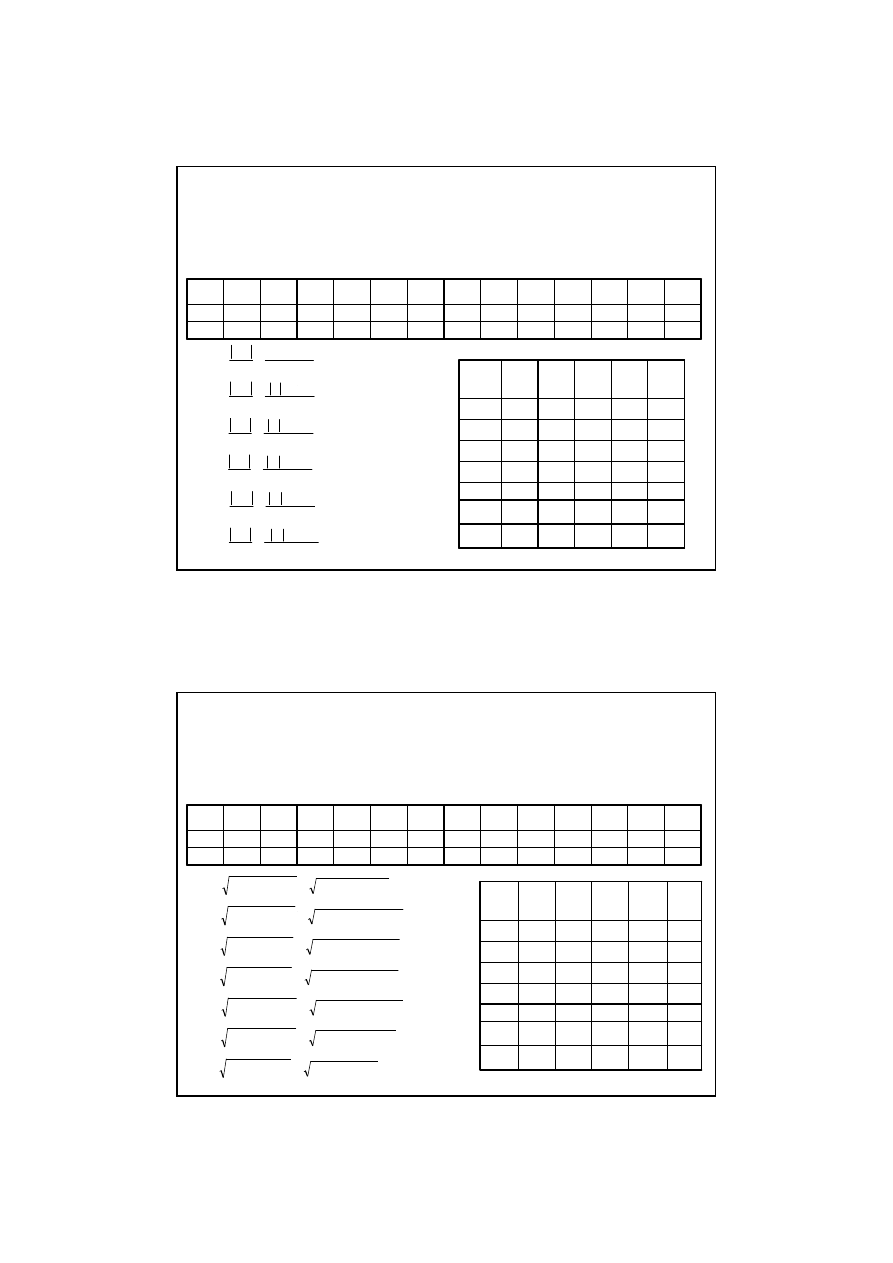
Krok 4 - Obliczenia i wypełnianie tablicy

wyników

oblicze

ń

– cz.1 - wska

ź

niki W

x

, W

o

100

65

50

30

mm

mm

mm

mm

d

3

d

2

=d

B

d

1

d

A

3

cm

53,8

W

2

W

,

3

cm

26,9

W

W

3

cm

2

,

196

1

,

98

2

W

2

W

3

cm

1

,

98

m

10

1

,

98

32

)

10

100

(

14

,

3

32

)

d

(

W

3

cm

53,8

W

2

W

,

3

cm

26,9

W

W

3

cm

53,8

26,9

2

W

2

W

3

cm

26,9

m

10

26,9

32

)

10

65

(

14

,

3

32

)

d

(

W

3

cm

24,6

W

2

W

,

3

cm

12,3

W

W

3

cm

24,6

12,3

2

W

2

W

3

cm

12,3

m

10

12,3

32

)

10

50

(

14

,

3

32

)

d

(

W

xJ

oJ

xF

xJ

xH

oH

3

6

3

3

3

3

xH

xG

oG

xF

xG

xF

oF

3

6

3

3

3

2

xF

xE

oE

xD

xE

xD

oD

3

6

3

3

3

1

xD

====

⋅⋅⋅⋅

====

====

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

====

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

====

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

−−−−

−−−−

−−−−

−−−−

−−−−

−−−−

ππππ

ππππ

ππππ

53,8

26,9

J

196,2

98,1

H

53,8

26,9

G

53,8

26,9

F

24,6

12,3

E

24,6

12,3

D

12,6

6,3

C

W

o

,

cm

3

W

x

,

cm

3

Przek-

rój

3

cm

6

,

12

3

,

6

2

W

2

W

3

cm

3

,

6

m

10

3

,

6

32

)

10

40

(

14

,

3

32

)

d

(

W

xC

oC

3

6

3

3

3

A

xC

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

−−−−

−−−−

ππππ

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych

i

skr

ę

canych

Przykład nr 2: Sprawdzi

ć

warunek

bezpiecze

ń

stwa

wału obci

ąż

onego

równocze

ś

nie

momen -

tami obrotowymi

M

1

,

M

2

i

M

3

oraz czynnymi siłami skupionymi

P

1

,

P

2

i

P

3

=

J

o

k

14

Krok 4 - Obliczenia i wypełnianie tablicy

wyników

oblicze

ń

– cz. 2 – napr

ęż

enia

σσσσ

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

-3

M

sH

0

M

sJ

1,6

M

gJ

0

M

sC

-1

M

sD

-1

M

sE

-3

M

sF

-3

M

sG

2,7

2,8

3,0

2,4

1,8

0,8

M

gH

M

gG

M

gF

M

gE

M

gD

M

gC

?

?

59,5

53,8

26,9

J

?

?

27,1

196,2

98,1

H

?

?

104,1

53,8

26,9

G

?

?

111,5

53,8

26,9

F

?

?

195,1

24,6

12,3

E

?

?

146,3

24,6

12,3

D

?

?

127,0

12,6

6,3

C

σσσσ

z

,

MPa

ττττ

,

MPa

σσσσ

,

MPa

W

o

,

cm

3

W

x

,

cm

3

Przek-

rój

MPa

1

,

104

Pa

10

1

,

104

6

10

9

,

26

3

10

8

,

2

W

M

MPa

5

,

111

Pa

10

5

,

111

6

10

9

,

26

3

10

0

,

3

W

M

MPa

1

,

195

Pa

10

1

,

195

6

10

3

,

12

3

10

4

,

2

W

M

MPa

3

,

146

Pa

10

3

,

146

6

10

3

,

12

3

10

8

,

1

W

M

MPa

0

,

27

1

Pa

10

0

,

127

6

10

3

,

6

3

10

8

,

0

W

M

6

xG

gG

G

6

xF

gF

F

6

xE

gE

E

6

xD

gD

D

6

xC

gC

C

====

⋅⋅⋅⋅

====

−−−−

⋅⋅⋅⋅

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

−−−−

⋅⋅⋅⋅

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

−−−−

⋅⋅⋅⋅

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

−−−−

⋅⋅⋅⋅

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

−−−−

⋅⋅⋅⋅

⋅⋅⋅⋅

====

====

σσσσ

====

====

σσσσ

====

====

σσσσ

====

====

σσσσ

====

====

σσσσ

8

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych

i

skr

ę

canych

Przykład nr 2: Sprawdzi

ć

warunek

bezpiecze

ń

stwa

wału obci

ąż

onego

równocze

ś

nie

momen -

tami obrotowymi

M

1

,

M

2

i

M

3

oraz czynnymi siłami skupionymi

P

1

,

P

2

i

P

3

=

J

o

k

15

Krok 4 - Obliczenia i wypełnianie tablicy

wyników

oblicze

ń

– cz.3 – napr

ęż

enia

ττττ

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

-3

M

sH

0

M

sJ

1,6

M

gJ

0

M

sC

-1

M

sD

-1

M

sE

-3

M

sF

-3

M

sG

2,7

2,8

3,0

2,4

1,8

0,8

M

gH

M

gG

M

gF

M

gE

M

gD

M

gC

?

0

59,5

53,8

26,9

J

?

15,3

27,1

196,2

98,1

H

?

55,8

104,1

53,8

26,9

G

?

55,8

111,5

53,8

26,9

F

?

40,7

195,1

24,6

12,3

E

?

40,7

146,3

24,6

12,3

D

?

0

127,0

12,6

6,3

C

σσσσ

z

,

MPa

ττττ

,

MPa

σσσσ

,

MPa

W

o

,

cm

3

W

x

,

cm

3

Przek-

rój

MPa

3

,

15

Pa

10

3

,

15

10

2

,

196

10

3

-

W

M

MPa

8

,

55

Pa

10

8

,

55

10

8

,

53

10

3

-

W

M

MPa

8

,

55

Pa

10

8

,

55

10

8

,

53

10

3

-

W

M

MPa

7

,

40

Pa

10

7

,

40

10

6

,

24

10

1

-

W

M

MPa

7

,

40

Pa

10

7

,

40

10

6

,

24

10

1

-

W

M

0

10

6

,

12

0

W

M

6

6

3

oH

sH

H

6

6

3

oG

sG

G

6

6

3

oF

sF

F

6

6

3

oE

sE

E

6

6

3

oD

sD

D

6

oC

sC

C

====

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

====

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

====

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

====

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

====

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

====

====

====

ττττ

====

====

====

ττττ

====

====

====

ττττ

====

====

====

ττττ

====

====

====

ττττ

====

====

====

ττττ

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych

i

skr

ę

canych

Przykład nr 2: Sprawdzi

ć

warunek

bezpiecze

ń

stwa

wału obci

ąż

onego

równocze

ś

nie

momen -

tami obrotowymi

M

1

,

M

2

i

M

3

oraz czynnymi siłami skupionymi

P

1

,

P

2

i

P

3

=

J

o

k

16

Krok 4 - Obliczenia i wypełnianie tablicy

wyników

oblicze

ń

– cz.4 – napr

ęż

enia

σσσσ

z

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

kNm

-3

M

sH

0

M

sJ

1,6

M

gJ

0

M

sC

-1

M

sD

-1

M

sE

-3

M

sF

-3

M

sG

2,7

2,8

3,0

2,4

1,8

0,8

M

gH

M

gG

M

gF

M

gE

M

gD

M

gC

59,5

0

59,5

53,8

26,9

J

37,9

15,3

27,1

196,2

98,1

H

142,0

55,8

104,1

53,8

26,9

G

147,6

55,8

111,5

53,8

26,9

F

207,4

40,7

195,1

24,6

12,3

E

162,4

40,7

146,3

24,6

12,3

D

127,0

0

127,0

12,6

6,3

C

σσσσ

z

,

MPa

ττττ

,

MPa

σσσσ

,

MPa

W

o

,

cm

3

W

x

,

cm

3

Przek-

rój

MPa

5

,

59

0

3

5

,

59

3

MPa

9

,

37

3

,

15

3

1

,

27

3

MPa

0

,

142

8

,

55

3

1

,

104

3

MPa

6

,

147

8

,

55

3

5

,

111

3

MPa

4

,

207

7

,

40

3

1

,

195

3

MPa

4

,

162

7

,

40

3

3

,

146

3

MPa

0

,

127

0

3

0

,

127

3

2

2

2

J

2

J

zJ

2

2

2

G

2

G

zH

2

2

2

G

2

G

zG

2

2

2

F

2

F

zF

2

2

2

E

2

E

zE

2

2

2

D

2

D

zD

2

2

2

C

2

C

zC

====

====

====

σσσσ

====

====

====

σσσσ

====

====

====

σσσσ

====

====

====

σσσσ

====

====

====

σσσσ

====

====

====

σσσσ

====

====

====

⋅⋅⋅⋅

++++

ττττ

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

++++

ττττ

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

++++

ττττ

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

++++

ττττ

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

++++

ττττ

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

++++

ττττ

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

++++

ττττ

⋅⋅⋅⋅

++++

σσσσ

σσσσ

9

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych

i

skr

ę

canych

Przykład nr 2: Sprawdzi

ć

warunek

bezpiecze

ń

stwa

wału obci

ąż

onego

równocze

ś

nie

momen -

tami obrotowymi

M

1

,

M

2

i

M

3

oraz czynnymi siłami skupionymi

P

1

,

P

2

i

P

3

=

J

o

k

17

Krok 5 - Sformułowanie

liczbowej

postaci warunku

bezpiecze

ń

stwa

oraz

wniosku

do uzyskanych wyników

MPa

207,4

)

,

,

,

,

,

,

max(

zJ

zH

zG

zF

zE

zD

zC

max

z

====

====

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

0

15,3

55,8

55,8

40,7

40,7

0

ττττ

, MPa

37,9

37,9

142,0

147,6

207,4

162,4

127,0

σσσσ

z

, MPa

59,5

27,1

104,1

111,5

195,1

146,3

127,0

σσσσ

, MPa

J

H

G

F

E

D

C

Przekrój

MPa

200

k

MPa

207,4

r

max

z

====

>>>>

====

σσσσ

Warunek

bezpiecze

ń

stwa

wału obci

ąż

onego

równocze

ś

nie

momentami i siłami jak na rysunku -

nie

jest

spełniony

Wniosek

Chocia

ż

maksymalne napr

ęż

enie

normalne

wału jest ok. 4 razy wi

ę

ksze ni

ż

maksymalne napr

ę

-

ż

enie

styczne

wału, to

nie

mo

ż

na

pomin

ąć

napr

ęż

enia

stycznego

przy sprawdzaniu warunku

bezpiecze

ń

stwa

, bo uzyskano by wtedy pozytywny wynik sprawdzenia, który byłby

niezgodny

z faktycznym

bezpiecze

ń

stwem

tego wału.

18

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych

i

skr

ę

canych

Przykład nr 3 –

Temat

:

=

J

o

k

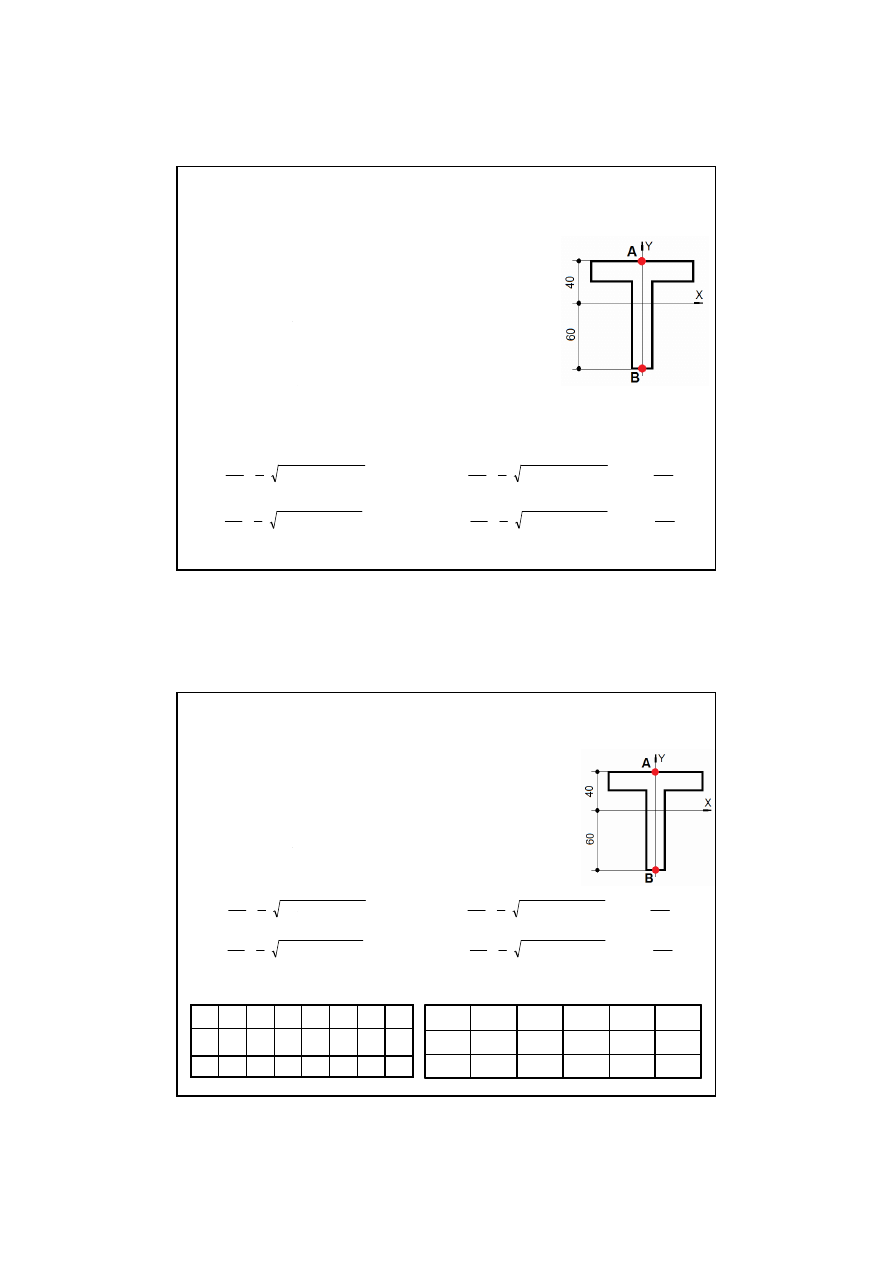
Wspornik instalacyjny o przekroju z osiami oboj

ę

tnymi X, Y jak na

rysunku i z osiowym momentem bezwładno

ś

ci J

X

= 335 cm

4

,

jest

wykonany z materiału

spr

ęż

ysto

-

kruchego

maj

ą

cego parametry

k

r

= 65 MPa,

νννν

= 0,25. Wykorzystuj

ą

c hipotez

ę

najwi

ę

kszego wyd -

łu

ż

enia jednostkowego

sprawdzi

ć

warunek

bezpiecze

ń

stwa

tego

wspornika, gdy jest on obci

ąż

ony ekstremalnym momentem

zgina

-

naj

ą

cym

M

X

= - 3 kNm oraz ma w punktach A i B przekrojów ekstre-

malne napr

ęż

enia

styczne

:

ττττ

A

= 20 MPa,

ττττ

B

= 15 MPa.

Cztery

kroki

obliczeniowe

1. Dobór i zestawienie

wzorów

do oblicze

ń

.

2. Tablica

danych

oraz szablon tablicy

wyników

oblicze

ń

.

3. Obliczenia i

wypełnianie

tablicy

wyników

oblicze

ń

.

4. Sformułowanie

liczbowej

postaci warunku

bezpiecze

ń

stwa

oraz

wniosku

do uzyskanych wyników.

10

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych

i

skr

ę

canych

Przykład nr 3 –

Temat

:

=

J

o

k

Wspornik instalacyjny o przekroju z osiami oboj

ę

tnymi X, Y jak na

rysunku i z osiowym momentem bezwładno

ś

ci J

X

= 335 cm

4

,

jest

wykonany z materiału

spr

ęż

ysto

-

kruchego

maj

ą

cego parametry

k

r

= 65 MPa,

νννν

= 0,25. Wykorzystuj

ą

c hipotez

ę

najwi

ę

kszego wyd -

łu

ż

enia jednostkowego

sprawdzi

ć

warunek

bezpiecze

ń

stwa

tego

wspornika, gdy jest on obci

ąż

ony ekstremalnym momentem

zgina

-

naj

ą

cym

M

X

= - 3 kNm oraz ma w punktach A i B przekrojów ekstre -

malne napr

ęż

enia

styczne

:

ττττ

A

= 20 MPa,

ττττ

B

= 15 MPa.

Krok 1 - dobór i zestawienie

wzorów

do oblicze

ń

.

B

X

X

B

2

B

2

B

B

B

3

B

2

2

B

2

B

B

B

1

Y

J

M

,

)

(

4

)

(

2

1

2

,

0

,

)

(

4

)

(

2

1

2

⋅⋅⋅⋅

−−−−

====

σσσσ

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

−−−−

σσσσ

====

σσσσ

====

σσσσ

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

++++

σσσσ

====

σσσσ

ττττ

ττττ

r

B

3

B

2

B

1

zB

r

A

3

A

2

A

1

zA

k

)

(

,

k

)

(

≤≤≤≤

σσσσ

++++

σσσσ

⋅⋅⋅⋅

νννν

−−−−

σσσσ

====

σσσσ

≤≤≤≤

σσσσ

++++

σσσσ

⋅⋅⋅⋅

νννν

−−−−

σσσσ

====

σσσσ

A

X

X

A

2

A

2

A

A

A

3

A

2

2

A

2

A

A

A

1

Y

J

M

,

)

(

4

)

(

2

1

2

,

0

,

)

(

4

)

(

2

1

2

⋅⋅⋅⋅

−−−−

====

σσσσ

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

−−−−

σσσσ

====

σσσσ

====

σσσσ

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

++++

σσσσ

====

σσσσ

ττττ

ττττ

19

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych

i

skr

ę

canych

Przykład nr 3 –

Temat

:

=

J

o

k

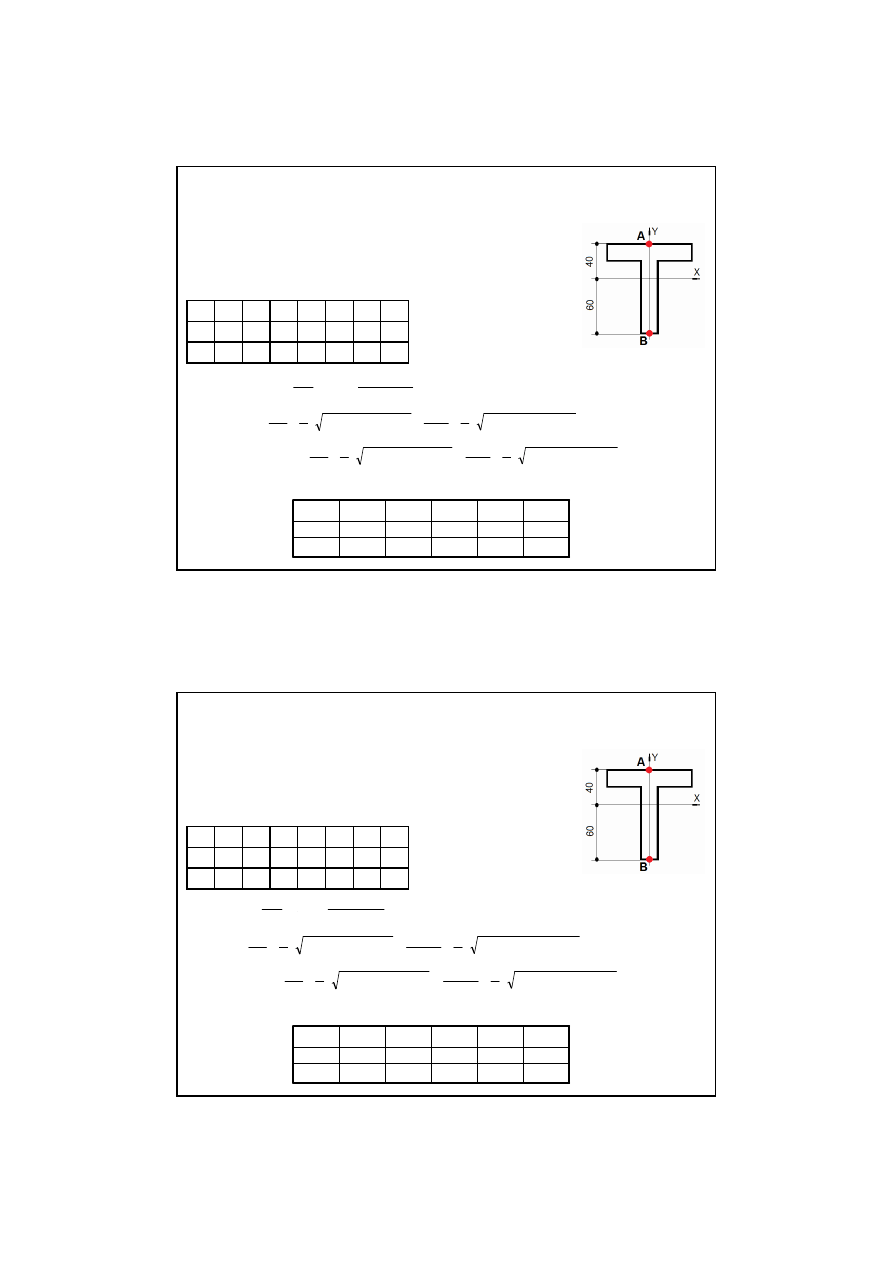
Wspornik instalacyjny o przekroju z osiami oboj

ę

tnymi X, Y jak na ry -

sunku jest wykonany z materiału

spr

ęż

ysto

-

kruchego

.

Wykorzystu -

j

ą

c hipotez

ę

najwi

ę

kszego wydłu

ż

enia jednostkowego

sprawdzi

ć

warunek

bezpiecze

ń

stwa

tego wspornika.

Krok 2 - tablica

danych

oraz szablon tablicy

wyników

oblicze

ń

.

0,25

÷

νννν

-60

40

15

20

-3

65

355

mm

mm

MPa

MPa

kNm

MPa

cm

4

Y

B

Y

A

ττττ

B

ττττ

A

M

X

k

r

J

X

?

?

?

?

?

B

?

?

?

?

?

A

σσσσ

z

,

MPa

σσσσ

3

,

MPa

σσσσ

2

,

MPa

σσσσ

1

,

MPa

σσσσ,

MPa

Punkt

B

X

X

B

2

B

2

B

B

B

3

B

2

2

B

2

B

B

B

1

A

X

X

A

2

A

2

A

A

A

3

A

2

2

A

2

A

A

A

1

Y

J

M

,

)

(

4

)

(

2

1

2

,

0

,

)

(

4

)

(

2

1

2

Y

J

M

,

)

(

4

)

(

2

1

2

,

0

,

)

(

4

)

(

2

1

2

⋅⋅⋅⋅

−−−−

====

σσσσ

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

−−−−

σσσσ

====

σσσσ

====

σσσσ

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

++++

σσσσ

====

σσσσ

⋅⋅⋅⋅

−−−−

====

σσσσ

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

−−−−

σσσσ

====

σσσσ

====

σσσσ

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

++++

σσσσ

====

σσσσ

ττττ

ττττ

ττττ

ττττ

r

B

3

B

2

B

1

zB

r

A

3

A

2

A

1

zA

k

)

(

,

k

)

(

≤≤≤≤

σσσσ

++++

σσσσ

⋅⋅⋅⋅

νννν

−−−−

σσσσ

====

σσσσ

≤≤≤≤

σσσσ

++++

σσσσ

⋅⋅⋅⋅

νννν

−−−−

σσσσ

====

σσσσ

11

21

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych

i

skr

ę

canych

Przykład nr 3 –

Temat

:

=

J

o

k

Wspornik instalacyjny o przekroju z osiami oboj

ę

tnymi X, Y jak na ry -

sunku jest wykonany z materiału

spr

ęż

ysto

-

kruchego

.

Wykorzystu -

j

ą

c hipotez

ę

najwi

ę

kszego wydłu

ż

enia jednostkowego

sprawdzi

ć

warunek

bezpiecze

ń

stwa

tego wspornika.

Krok 3 - obliczenia i

wypeł -

nianie

tablicy

wyników

ob -

licze

ń

- cz.1 – napr

ęż

enia

w punkcie A

0,25

÷

νννν

-60

40

15

20

-3

65

355

mm

mm

MPa

MPa

kNm

MPa

cm

4

Y

B

Y

A

ττττ

B

ττττ

A

M

X

k

r

J

X

?

?

?

?

?

B

45,5

-9,3

0

43,1

33,8

A

σσσσ

z

,

MPa

σσσσ

3

,

MPa

σσσσ

2

,

MPa

σσσσ

1

,

MPa

σσσσ,

MPa

Punkt

MPa

45,5

9,3)

-

(0

0,25

-

43,1

)

(

MPa

-9,3

)

20

(

4

)

8

,

33

(

2

1

2

8

,

33

)

(

4

)

(

2

1

2

,

0

MPa

43,1

)

20

(

4

)

8

,

33

(

2

1

2

8

,

33

)

(

4

)

(

2

1

2

MPa

8

,

33

Pa

10

8

,

33

10

40

10

355

10

3

Y

J

M

A

3

A

2

A

1

zA

2

2

2

A

2

A

A

A

3

A

2

2

2

2

A

2

A

A

A

1

6

3

8

3

A

X

X

A

====

⋅⋅⋅⋅

====

σσσσ

++++

σσσσ

⋅⋅⋅⋅

νννν

−−−−

σσσσ

====

σσσσ

====

⋅⋅⋅⋅

++++

⋅⋅⋅⋅

−−−−

====

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

−−−−

σσσσ

====

σσσσ

====

σσσσ

====

⋅⋅⋅⋅

++++

⋅⋅⋅⋅

++++

====

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

++++

σσσσ

====

σσσσ

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

−−−−

−−−−

====

⋅⋅⋅⋅

−−−−

====

σσσσ

ττττ

ττττ

−−−−

−−−−

22

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych

i

skr

ę

canych

Przykład nr 3 –

Temat

:

=

J

o

k

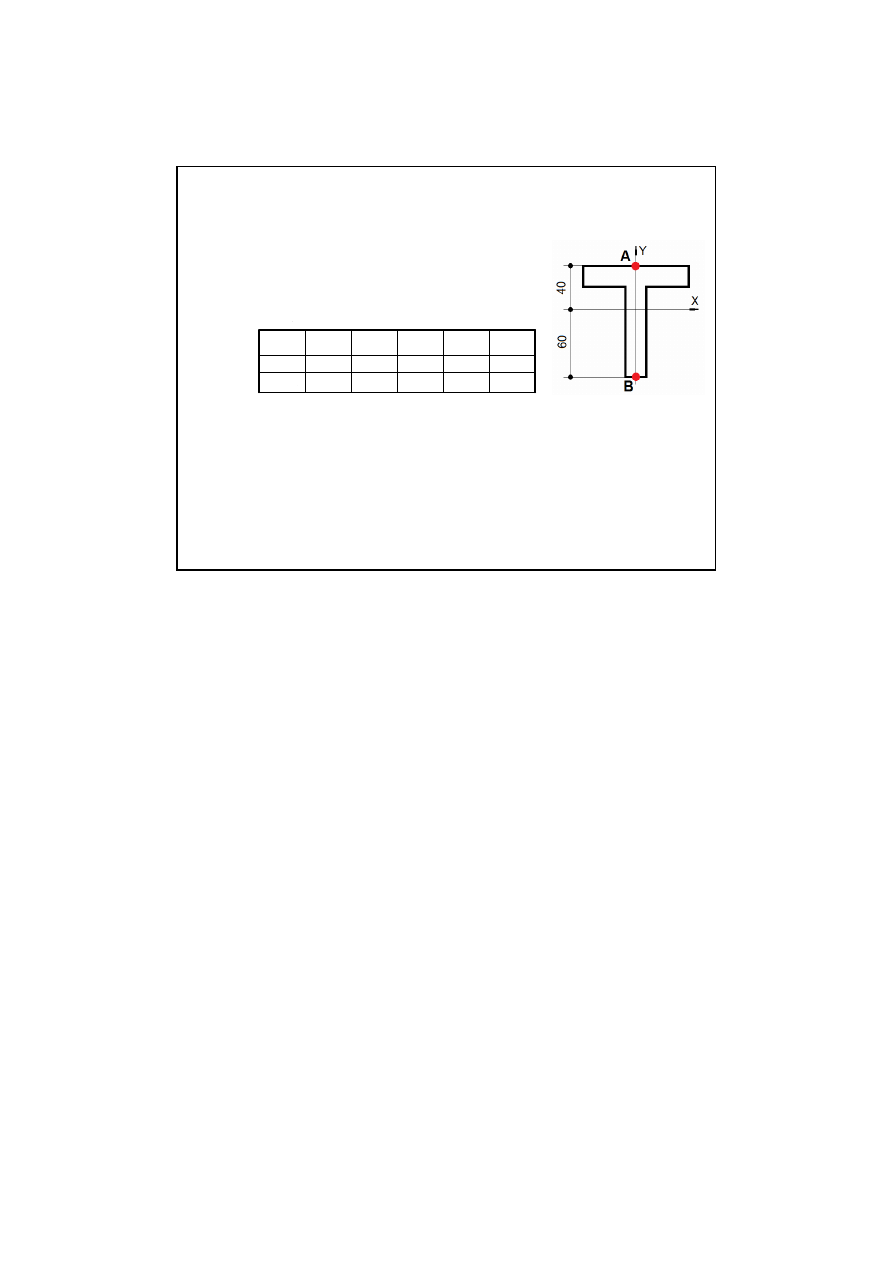
Wspornik instalacyjny o przekroju z osiami oboj

ę

tnymi X, Y jak na ry -

sunku jest wykonany z materiału

spr

ęż

ysto

-

kruchego

.

Wykorzystu -

j

ą

c hipotez

ę

najwi

ę

kszego wydłu

ż

enia jednostkowego

sprawdzi

ć

warunek

bezpiecze

ń

stwa

tego wspornika.

Krok 3 - obliczenia i

wypeł -

nianie

tablicy

wyników

ob -

licze

ń

- cz.2 - napr

ęż

enia

w punkcie B

0,25

÷

νννν

-60

40

15

20

-3

65

355

mm

mm

MPa

MPa

kNm

MPa

cm

4

Y

B

Y

A

ττττ

B

ττττ

A

M

X

k

r

J

X

17,8

-54,8

0

4,1

-50,7

B

45,5

-9,3

0

43,1

33,8

A

σσσσ

z

,

MPa

σσσσ

3

,

MPa

σσσσ

2

,

MPa

σσσσ

1

,

MPa

σσσσ,

MPa

Punkt

MPa

8

,

7

1

54,8)

(0

0,25

-

4,1

)

(

MPa

-54,8

)

15

(

4

)

7

,

50

(

2

1

2

7

,

50

)

(

4

)

(

2

1

2

,

0

MPa

4,1

)

15

(

4

)

7

,

50

(

2

1

2

7

,

50

)

(

4

)

(

2

1

2

MPa

7

,

50

Pa

10

7

,

50

10

)

60

(

10

355

10

3

Y

J

M

AB

3

B

2

B

1

zB

2

2

2

B

2

B

B

B

3

B

2

2

2

2

B

2

B

B

B

1

6

3

8

3

B

X

X

B

====

−−−−

⋅⋅⋅⋅

====

σσσσ

++++

σσσσ

⋅⋅⋅⋅

νννν

−−−−

σσσσ

====

σσσσ

====

⋅⋅⋅⋅

++++

−−−−

⋅⋅⋅⋅

−−−−

−−−−

====

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

−−−−

σσσσ

====

σσσσ

====

σσσσ

====

⋅⋅⋅⋅

++++

−−−−

⋅⋅⋅⋅

++++

−−−−

====

⋅⋅⋅⋅

++++

σσσσ

⋅⋅⋅⋅

++++

σσσσ

====

σσσσ

−−−−

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

−−−−

−−−−

====

⋅⋅⋅⋅

−−−−

====

σσσσ

ττττ

ττττ

−−−−

−−−−

12

23

Ć

wiczenie T9 – cz

ęść

2

Obliczanie napr

ęż

e

ń

maksymalnych dla pr

ę

tów

równocze

ś

nie

zginanych

i

skr

ę

canych

Przykład nr 3 –

Temat

:

=

J

o

k

Wspornik instalacyjny jak na rysunku

,

jest wykonany z materiału

spr

ęż

ysto -

kruchego

maj

ą

cego k

r

= 65 MPa.

Sprawdzi

ć

waru -

nek

bezpiecze

ń

stwa

tego wspornika, gdy jest on obci

ąż

ony mo -

mentem

zginaj

ą

cym

M

X

= -3 kNm oraz ma w punktach A i B

przekrojów napr

ęż

enia

styczne

:

ττττ

A

= 20 MPa,

ττττ

B

= 15 MPa.

Krok 4 - Sformułowanie

liczbowej

postaci warunku

bezpiecze

ń

stwa

oraz

wniosku

do uzyskanych wyników.

MPa

65

k

MPa

8

,

17

,

MPa

65

k

MPa

5

,

45

r

zB

r

zA

====

<<<<

====

σσσσ

====

<<<<

====

σσσσ

17,8

-54,8

0

4,1

-50,7

B

45,5

-9,3

0

43,1

33,8

A

σσσσ

z

,

MPa

σσσσ

3

,

MPa

σσσσ

2

,

MPa

σσσσ

1

,

MPa

σσσσ,

MPa

Punkt

Tablica

wyników

Warunek bezpiecze

ń

stwa wspornika jest spełniony

Wniosek

Wpływ napr

ęż

e

ń

stycznych

analizowanego wspornika na jego warunek

bezpiecze

ń

stwa

jest ekwiwalentny do

powi

ę

kszenia

momentu

zginaj

ą

cego

M

x

o ok. 35%.