1
1
Materiały dydaktyczne zawieraj
ą
ce 19 slajdów na 10 stronach,
dotycz
ą
ce
ć
wiczenia T4 z przedmiotu „Wytrzymało
ść
materiałów”,
przeznaczone
dla studentów II roku studiów I stopnia w kierunku „Energetyka”
na wydz. Energetyki i Paliw w AGH
Autor materiałów i osoba prowadz
ą
ca
ć
wiczenia:
Marek Płachno, dr hab. in
ż
., prof. AGH
Autor nie wyra
ż
a zgody na inne wykorzystywanie tych materiałów,
ni
ż
podane w ich przeznaczeniu.
Ć
wiczenie T4
Temat:
Analiza stanu napr
ęż
enia i odkształcenia w materiale elementu konstrukcji
Na
ć
wiczeniu T4 studenci poznaj
ą
wa
ż
ny
przypadek
analizy wytrzymało
ś
ciowej
dotycz
ą
cy tej analizy w punkcie materiału nale
żą
cym nie
tylko
do wskazanej
powierzchni
przekroju
pr
ę
ta, ale
te
ż
do
obj
ę
to
ś
ci
materiału w
bliskim otoczeniu
tego punktu.
Przykład nr 1. –
Temat
Obliczy
ć
warto
ś
ci
i
kierunki
dla ekstremalnych
napr
ęż
e
ń
rozci
ą
gaj
ą
cych
oraz
ś
ciskaj
ą
cych -
tj.
napr
ęż
e
ń
głównych,
a tak
ż
e kierunki i warto
ś
ci ekstremalnych napr
ęż
e
ń
stycznych
w punk-
cie obj
ę
to
ś
ci materiału maj
ą
cym
płaski
stan napr
ęż
e
ń
o parametrach wyra
ż
onych w
ogólnej
postaci jako
σσσσ
x
= 150 MPa,
σσσσ
y
= -250 MPa,
ττττ
xy
= -240 MPa.
Nowe
poj
ę
cia dotycz
ą
ce
tematu
zadania:
1. Definicje i oznaczenia
ogólnej postaci
parametrów dla
przestrzennego
stanu napr
ęż
e
ń
w punkcie obj
ę
to
ś
ci materiału.
2. Definicje i oznaczenia
napr
ęż
e
ń
głównych
i
kierunków
głównych
dla
przestrzennego
stanu napr
ęż
e
ń
jw
.
3. Oznaczenia
napr
ęż
e
ń
głównych
i
kierunków
głównych
dla
płaskiego
i
jednoosiowego
stanu napr
ęż
e
ń
jw.
4. Zale
ż
no
ś
ci algebraiczne do obliczania warto
ś
ci i kierunków
napr
ęż
e
ń
głównych
oraz
warto
ś
ci i kierunków ekstremalnych
napr
ęż
e
ń
stycznych
dla parametrów
płaskiego
stanu napr
ęż
e
ń
wyra
ż
onych w
postaci ogólnej
.
2
2
Ć
wiczenie T4 - Przykład nr 1
Obliczy
ć
warto
ś
ci
i
kierunki
dla ekstremalnych
napr
ęż
e
ń
rozci
ą
gaj
ą
cych,
ś
ciskaj
ą
cych
oraz
stycznych
w punkcie obj
ę
to
ś
ci materiału maj
ą
cym
płaski stan
napr
ęż
e
ń
o parametrach
σσσσ
x
= 150 MPa,
σσσσ
y
= -250 MPa,
ττττ
xy
= -240 MPa
1.
Szablon
tablicy
wyników oblicze
ń
.
2.
Schemat
elementarnego prostok
ą
ta
EPT
dla analizowanego stanu napr
ęż
e
ń
.
3.
Obliczenia
i wpisanie wyników
oblicze
ń
do
tablicy
tych wyników.
4.
Ilustracja
warto
ś
ci
i
kierunków
napr
ęż
e
ń
głównych
na schemacie
EPT
.
Cztery
kroki
post
ę
powania
obliczeniowego:
σσσσ
3180
σσσσ
3135
σσσσ
390
σσσσ
345
σσσσ
3
ττττ
E135
ττττ
E90
ττττ
E45
ττττ
E
ττττ
E-45
Warto
ś
ci napr
ęż
e
ń
α
αα
α
t
+ 135°
α
αα
α
t +
90°
α
αα
α
t
+ 45°
α
αα
α
t
α
αα
α
t
- 45°
K
ą
t
α
αα
α
tn
wzgl
ę
dem osi x
Warto
ś
ci napr
ęż
e
ń
Parametry napr
ęż
e
ń
stycznych
Parametry napr
ęż
e
ń
normalnych
σσσσ
2180
σσσσ
1180
α
αα
α
1
+ 180°
σσσσ
2135
σσσσ
1135
α
αα
α
1
+ 135°
σσσσ
290
σσσσ
190
α
αα
α
1
+ 90°
σσσσ
245
σσσσ
145
α
αα
α
1
+ 45°
σσσσ
2
σσσσ
1
α
αα
α
1
K
ą
t
α
αα
α
1n
wzgl
ę
dem osi x
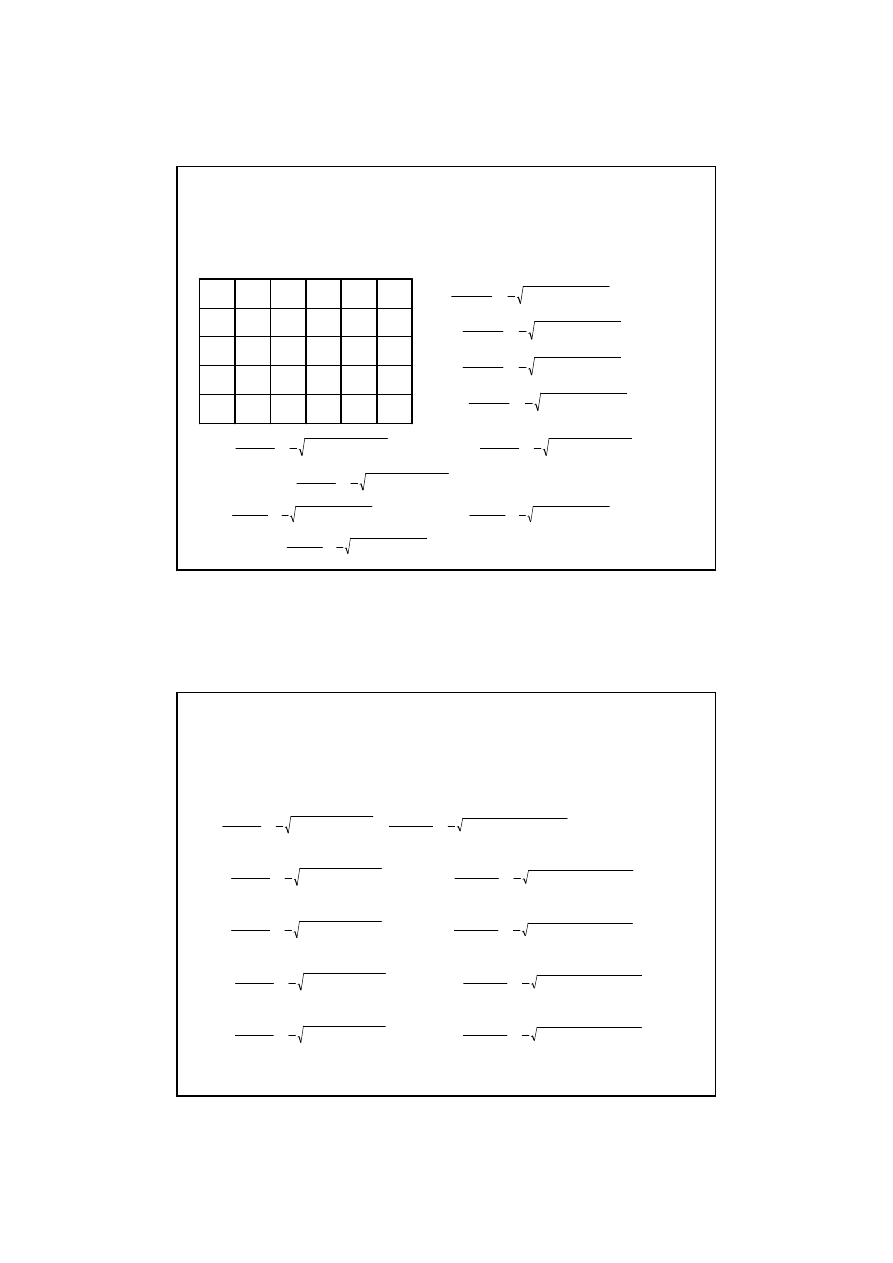
Krok 1 -
Szablon
tablicy
wyników oblicze
ń
σσσσ
1
≥
σσσσ
2
≥
σσσσ
3
–
napr
ęż
enie
główne
działaj
ą
ce w
kierunku
głównym
odpowiednio
1
,
2
i
3
,
σσσσ
145
≥
σσσσ
245
≥
σσσσ
345
–
napr
ęż
enie
działaj
ą
ce
pod k
ą
tem
45° do
kierunku
głównego
odpow.
1
,
2
i
3
.
4
Ć
wiczenie T4 - Przykład nr 1
Krok 2.
Schemat
elementarnego prostok
ą
ta
EPT
dla analizowanego stanu napr
ęż
e
ń
.
Cz
ęść
1. Zasady sporz
ą
dzania schematu
EPT
dla
płaskiego
stanu napr
ęż
e
ń
we
wskazanym
punkcie obj
ę
to
ś
ci materiału
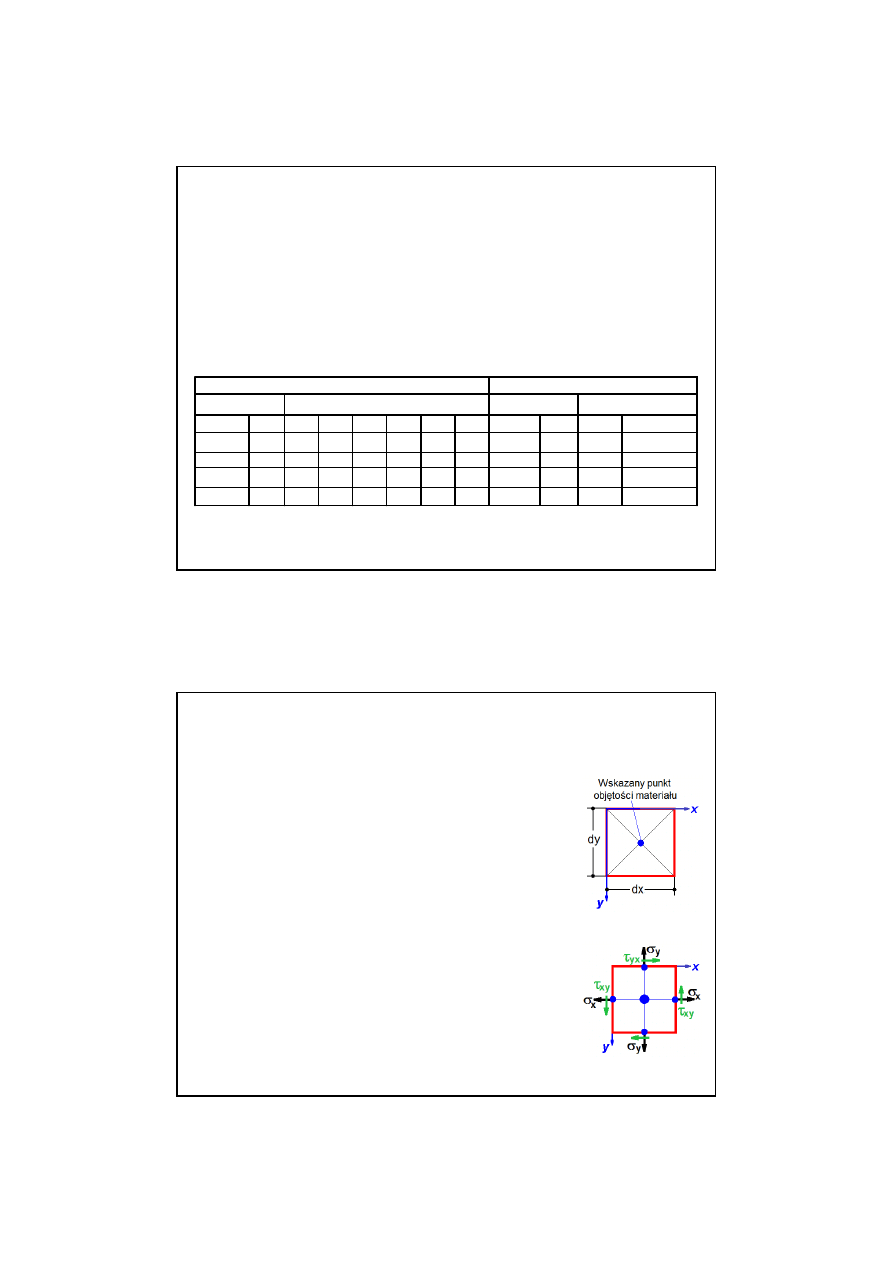
1). We
wskazanym
punkcie obj
ę
to
ś
ci materiału umieszcza si
ę
my
ś
-
lowo
ś
rodek geometryczny
prostok
ą
ta o bokach dx i dy tak, aby
kierunki
x
,
y
, napr
ęż
e
ń
normalnych
σσσσ
x
,
σσσσ
y
analizowanego stanu
pokrywały si
ę
z bokami tego prostok
ą
ta.
2). Do
ś
rodków
długo
ś
ci
boków prostok
ą
ta przykłada si
ę
wektory
napr
ęż
enia
σσσσ
x
i
σσσσ
y
oraz
wektory
napr
ęż
enia
ττττ
xy
i
ττττ
yx
.
3).
Wektory
ττττ
xy
przykłada si
ę
z przeciwnymi zwrotami do boków
EPT
maj
ą
cych kierunek osi
y
. Gdy napr
ęż
enie
ττττ
xy
jest dodatnie, to
zwrot
wektora
ττττ
xy
przy boku pokrywaj
ą
cyo
ś
y
jest zgodny z t
ą
osi
ą
, natomiast jest przeciwny, gdy napr
ęż
enie
ττττ
xy
jest ujemne.
4).
Wektory
ττττ
yx
przykłada si
ę
z przeciwnymi zwrotami do boków
EPT
maj
ą
cych kierunek osi
x
. Je
ż
eli napr
ęż
enie
ττττ
xy
jest dodatnie, to
zwrot
wektora
ττττ
yx
przy boku pokrywaj
ą
cym o
ś
x
jest zgodny z t
ą
osi
ą
, natomiast jest przeciwny, gdy napr
ęż
enie
ττττ
xy
jest ujemne.
Wektory napr
ęż
enia
σσσσ
x
i
σσσσ
y
rozci
ą
gaj
ą
EPT
, gdy to napr
ęż
enie jest
dodatnie, natomiast
ś
ciskaj
ą
, gdy jest ujemne.
3
5
Ć
wiczenie T4 - Przykład nr 1
Obliczy
ć
warto
ś
ci
i
kierunki
dla najwi
ę
kszych
napr
ęż
e
ń
rozci
ą
gaj
ą
cych
,
ś
ciskaj
ą
cych
oraz
stycznych
w punkcie obj
ę
to
ś
ci materiału maj
ą
cym
płaski stan
napr
ęż
e
ń
o parametrach wyra
ż
onych w postaci ogólnej:
.
MPa
240
,
MPa
250
,
MPa
150
xy
y
x
−
=
−
=
=
τ
σ
σ
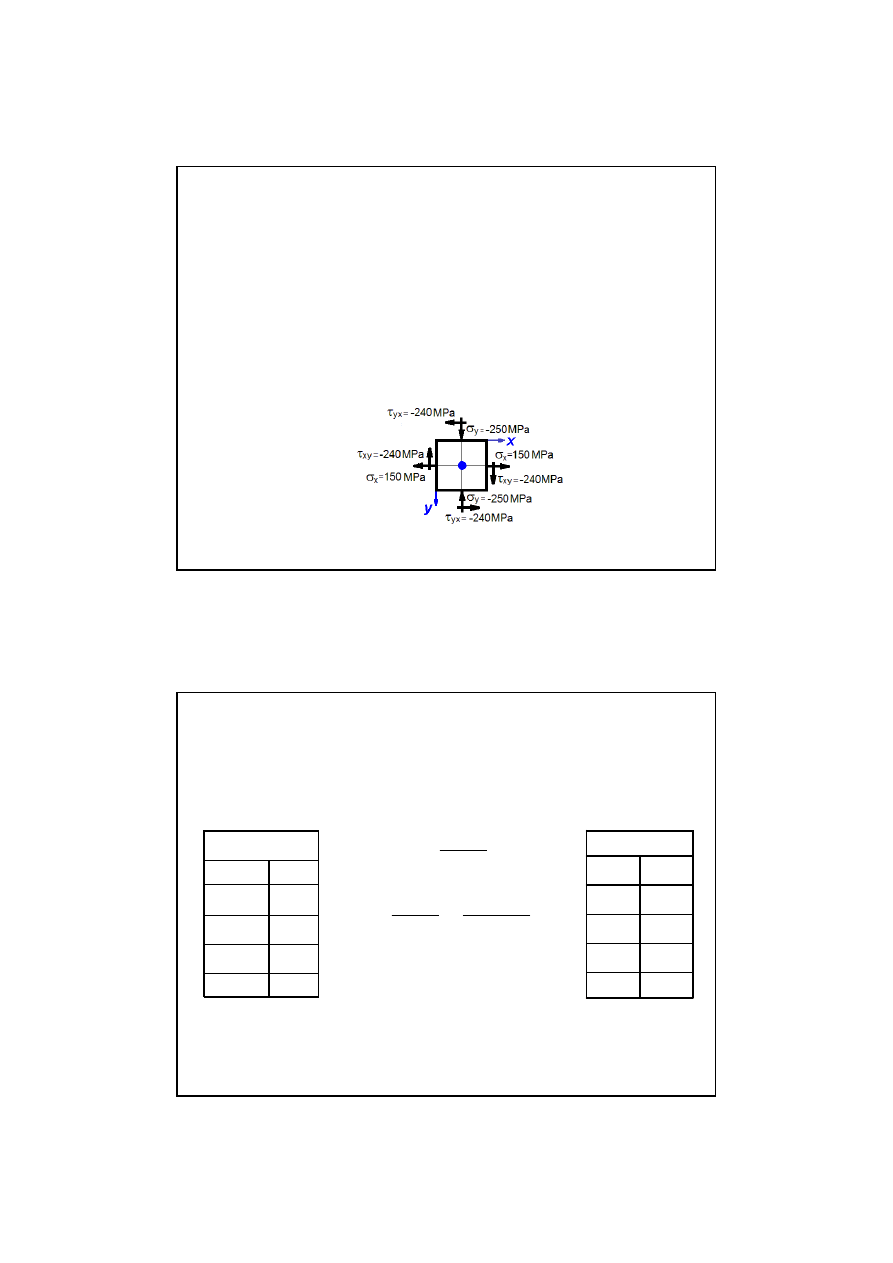
Krok 2.
Schemat
elementarnego go prostok
ą
ta
EPT
dla analizowanego stanu napr
ęż
e
ń
Cz.2. Sporz
ą
dzania schematu
EPT
dla
płaskiego
stanu napr
ęż
e
ń
zadanego w przykładzie 1
6
Ć
wiczenie T4 - Przykład nr 1
Krok 3 –
Obliczenia
i
wpisanie
wyników
oblicze
ń
do
tablicy
tych wyników.
y
x
xy
1n
2
tg2
σ
σ
α
−
−
=
τ
?
α
αα
α
1
α
αα
α
1
+ 180°
α
αα
α
1
+ 135°
α
αα
α
1
+ 90°
α
αα
α
1
+ 45°
?
?
?
?
K
ą
t
α
αα
α
1n
wzgl
ę
dem
osi x
Cz
ęść
1 – Obliczenie kierunków
napr
ęż
e
ń
głównych
dla płaskiego stanu napr
ęż
e
ń
o parametrach
σσσσ
x
= 150 MPa,
σσσσ
y
= -250 MPa,
ττττ
xy
= -240 MPa.
Nale
ż
y
obliczy
ć
:
Wzór
do oblicze
ń
:
(
)
(
)
o
o
o
o
90
n
25,1
2
1,
⋅
±
⇒
⋅
±
=
−
−
−
⋅
=
α
=
α
σ
σ
α
−
=
−
−
=
τ
n
1
n
1
y
x
xy
n
1
180
n
50,2
2
250
150
240
2
2
tg2
205°
α
αα
α
1
+ 180°
160°
α
αα
α
1
+ 135°
115°
α
αα
α
1
+ 90°
70°
α
αα
α
1
+ 45°
25°
α
αα
α
1
K
ą
t
α
αα
α
1n
wzgl
ę
dem
osi x
Obliczenia
:
Wyniki
oblicze
ń
:
o
25
1
≈
=
α
=
0)
(n
n
1
α
αα
α
Ekstremalnych
napr
ęż
e
ń
rozci
ą
gaj
ą
cych
i
ś
ciskaj
ą
cych
nale
ż
y spodziewa
ć
si
ę
w kierunkach okre
ś
lonych wzgl
ę
dem osi x przez k
ą
t
α
αα
α
1
równy ok. 25° oraz przez
ka
ż
dy k
ą
t wi
ę
kszy lub mniejszy od
α
αα
α
1
o krotno
ść
90°.
4
7
Ć
wiczenie T4 - Przykład nr 1
Krok 3 –
Obliczenia
i
wpisanie
wyników
oblicze
ń
do
tablicy
tych wyników
Cz
ęść
2 – Wzory dla
napr
ęż
e
ń
normalnych
w kierunkach
α
αα
α
1
+n·45°
wzgl
ę
dem osi x
płaskiego stanu napr
ęż
e
ń
:
σσσσ
x
= 150 MPa,
σσσσ
y
= -250 MPa,
ττττ
xy
= -240 MPa
Nale
ż
y
obliczy
ć
:
Wzory
do oblicze
ń
:
?
?
?
?
?
σσσσ
3135
σσσσ
390
σσσσ
345
σσσσ
3
σσσσ
3
?
σσσσ
2180
?
σσσσ
1180
?
σσσσ
2135
?
σσσσ
1135
?
σσσσ
290
?
σσσσ
190
?
σσσσ
245
?
σσσσ
145
?
σσσσ
2
?
σσσσ
1
)
45
n
2
cos(
4
)
(
2
1
2
)
90
2
cos(
4
)
(
2
1
2
)
45
2
cos(
4
)
(
2
1
2
)
0
2
cos(
4
)
(
2
1
2
2
xy
2
y
x
y
x
2
xy
2
y
x
y
x
2
xy
2
y
x
y
x
2
xy
2
y
x
y
x
o
o
o
o
⋅
⋅
⋅
+
−
+
+
⋅
⋅
+
−
+
+
⋅
⋅
+
−
+
+
⋅
⋅
+
−
+
+
=
τ
σ
σ
σ
σ
=
τ
σ
σ
σ
σ
=
τ
σ
σ
σ
σ
=
τ
σ
σ
σ
σ
⋅
45
1n
σσσσ
σσσσ
σσσσ
σσσσ
190
145
1
,
0
4
)
(
2
1
2
gdy
,
,
0
4
)
(
2
1
2
gdy
),
45
n
2
cos(
4
)
(
2
1
2
2
xy
2
y
x
y
x
2
xy
2
y
x
y
x
2
xy
2
y
x
y
x
<
+
−
−
+
=
≥
+
−
−
+
⋅
⋅
⋅
+
−
−
+
=
τ
σ
σ
σ
σ
τ
σ
σ
σ
σ
τ
σ
σ
σ
σ
⋅
⋅
0
lub
45
2n
45
2n
σσσσ
σσσσ
0
lub
45
3n
45
3n
0.
4
)
(
2
1
2
gdy
,
0,
4
)
(
2
1
2
gdy
),
45
n
2
cos(
4
)
(
2
1
2
2
xy
2
y
x
y
x
2
xy
2
y
x
y
x
2
xy
2
y
x
y
x
>
+
−
−
+
=
<
+
−
−
+
⋅
⋅
⋅
+
−
−
+
=
τ
σ
σ
σ
σ
τ
σ
σ
σ
σ
τ
σ
σ
σ
σ
⋅
⋅
σσσσ
σσσσ
o
8
Ć
wiczenie T4 - Przykład nr 1
Krok 3 –
Obliczenia
i
wpisanie
wyników
oblicze
ń
do
tablicy
tych wyników
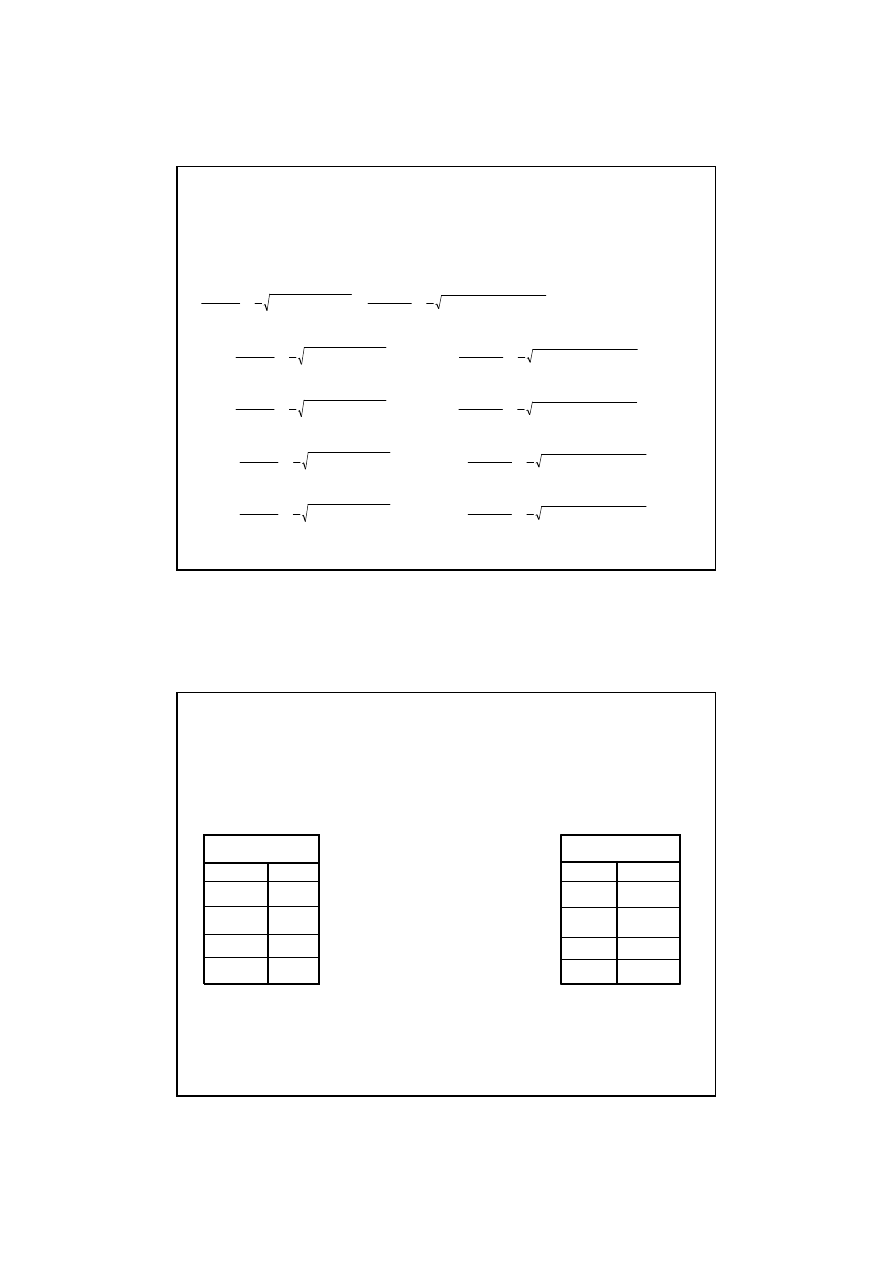
Cz
ęść
3 – Obliczenie
napr
ęż
e
ń
σσσσ
1n·45
w kierunkach
α
αα
α
1
+n·45°
okre
ś
lonych wzgl
ę
dem osi x
płaskiego stanu napr
ęż
e
ń
:
σσσσ
x
= 150 MPa,
σσσσ
y
= -250 MPa,
ττττ
xy
= -240 MPa
MPa.
262,4
MPa
50
MPa
362,4
MPa
50
MPa
262,4
1180
1135
190
145
1
=
=
⋅
+
+
+
−
=
⋅
⋅
+
−
+
+
−
=
=
⋅
+
+
+
−
=
⋅
⋅
+
−
+
+
−
=
=
⋅
+
+
+
−
=
⋅
⋅
+
−
+
+
=
=
⋅
+
+
+
−
=
⋅
⋅
+
−
+
+
=
=
+
+
+
−
=
+
−
+
+
τ
σ
σ
σ
σ
=
τ
σ
σ
σ
σ
=
τ
σ
σ
σ
σ
=
τ
σ
σ
σ
σ
=
τ
σ
σ
σ
σ
=
−
o
o
o
o
o
o
o
o
360
cos
4(-240)
)
250
150
(
2
1
2
250
150
)
180
2
cos(
4
)
(
2
1
2
270
cos
4(-240)
)
250
150
(
2
1
2
250
150
)
135
2
cos(
4
)
(
2
1
2
,
180
cos
4(-240)
)
250
150
(
2
1
2
250
150
)
90
2
cos(
4
)
(
2
1
2
,
90
cos
4(-240)
)
250
150
(
2
1
2
250
150
)
45
2
cos(
4
)
(
2
1
2
,
4(-240)
)
250
150
(
2
1
2
250
150
4
)
(
2
1
2
2
2
2
xy
2
y
x
y
x
2
2
2
xy
2
y
x
y
x
2
2
2
xy
2
y
x
y
x
2
2
2
xy
2
y
x
y
x
2
2
2
xy
2
y
x
y
x
,
σσσσ
σσσσ
σσσσ
σσσσ
σσσσ
5
9
Ć
wiczenie T4 - Przykład nr 1
Krok 3 –
Obliczenia
i
wpisanie
wyników
oblicze
ń
do
tablicy
tych wyników
Cz
ęść
4 – Obliczenie
napr
ęż
e
ń
σσσσ
2n·45
i
σσσσ
3n
·
45
w kierunkach
α
αα
α
1
+n·45°
okre
ś
lonych wzgl
ę
-
dem osi x stanu napr
ęż
e
ń
σσσσ
x
= 150 MPa,
σσσσ
y
= -250 MPa,
ττττ
xy
= -240 MPa
MPa.
362,4
MPa,
50
MPa,
262,4
MPa,
50
MPa,
362,4
:
dlatego
MPa
362,4
3180
3135
390
345
3
45
2n
0
−
=
=
⋅
+
+
+
−
=
⋅
⋅
+
−
+
+
−
=
=
⋅
+
+
+
−
=
⋅
⋅
+
−
+
+
=
=
⋅
+
+
−
−
=
⋅
⋅
+
−
−
+
−
=
=
⋅
+
+
−
−
=
⋅
⋅
+
−
−
+
−
<
−
=
+
+
−
−
=
+
−
−
+
τ
σ
σ
σ
σ
=
τ
σ
σ
σ
σ
=
τ
σ
σ
σ
σ
=
τ
σ
σ
σ
σ
=
=
=
τ
σ
σ
σ
σ
⋅
o
o
o
o
o
o
o
o
360
cos
4(-240)
)
250
150
(
2
1
2
250
150
)
180
2
cos(
4
)
(
2
1
2
270
cos
4(-240)
)
250
150
(
2
1
2
250
150
)
135
2
cos(
4
)
(
2
1
2
180
cos
4(-240)
)
250
150
(
2
1
2
250
150
)
90
2
cos(
4
)
(
2
1
2
90
cos
4(-240)
)
250
150
(
2
1
2
250
150
)
45
2
cos(
4
)
(
2
1
2
,
0
4(-240)
)
250
150
(
2
1
2
250
150
4
)
(
2
1
2
2
2
2
xy
2
y
x
y
x
2
2
2
xy
2
y
x
y
x
2
2
2
xy
2
y
x
y
x
2
2
2
xy
2
y
x
y
x
2
2
2
xy
2
y
x
y
x
oraz
σσσσ
σσσσ
σσσσ
σσσσ
σσσσ
σσσσ
10
Ć
wiczenie T4 - Przykład nr 1
Krok 3 –
Obliczenia
i
wpisanie
wyników
oblicze
ń
do
tablicy
tych wyników.
(
)
o
o
o
45
0
n
1
tn
t
1n
tn
)
(
90
n
45
+
α
=
α
=
α
⋅
±
+
α
α
=
=
?
α
αα
α
t
- 45°
α
αα
α
t
+ 135°
α
αα
α
t +
90°
α
αα
α
t
+ 45°
α
αα
α
t
?
?
?
?
K
ą
t
α
αα
α
tn
wzgl
ę
dem
osi x
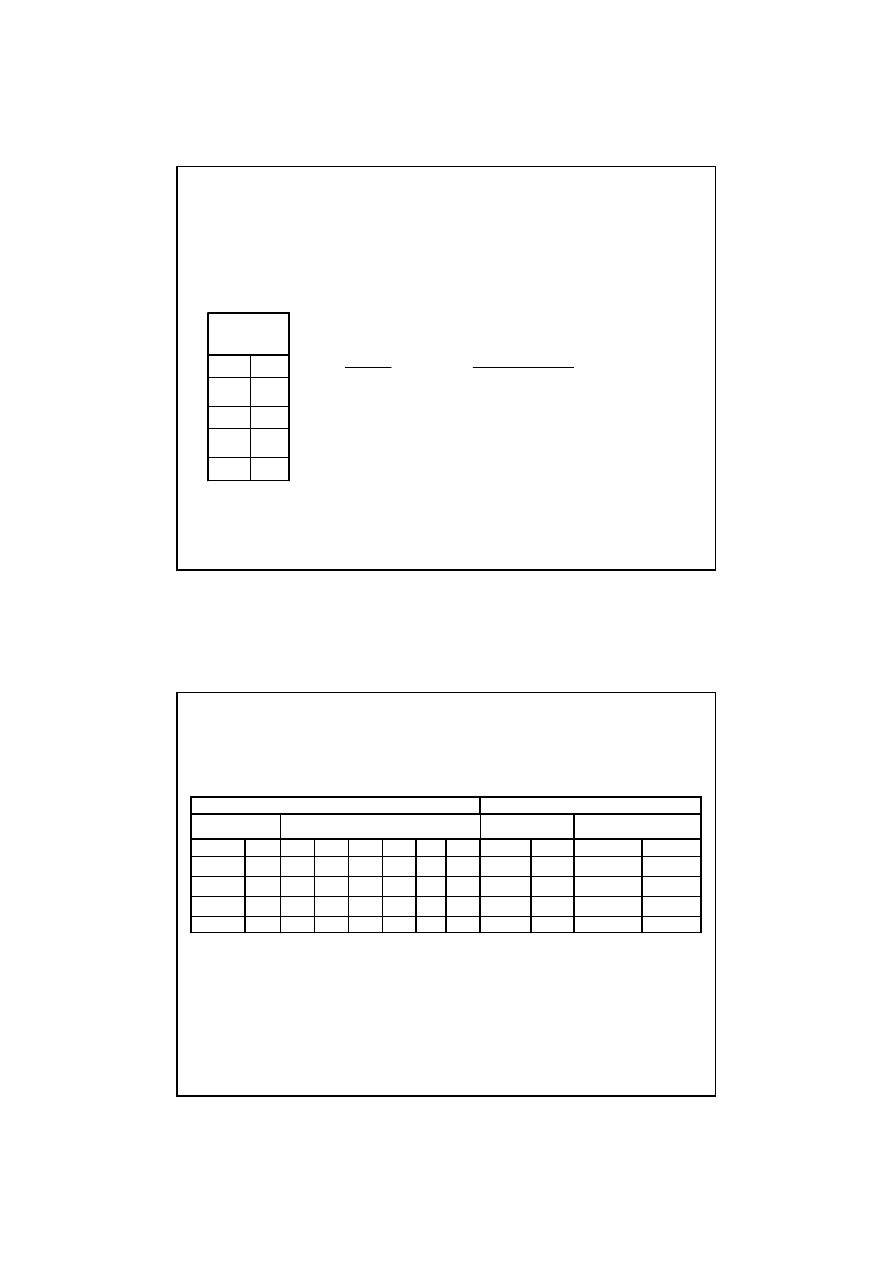
Cz
ęść
5 – Obliczenie kierunków dla ekstremalnych
napr
ęż
e
ń
stycznych
płaskiego
stanu napr
ęż
e
ń
o parametrach:
σσσσ
x
= 150 MPa,
σσσσ
y
= -250 MPa,
ττττ
xy
= -240 MPa
Nale
ż
y
obliczy
ć
:
Wzór
do oblicze
ń
:
205°
α
αα
α
t
+ 135°
160
α
αα
α
t +
90°
115°
α
αα
α
t
+ 45°
70°
α
αα
α
t
25°
α
αα
α
t
- 45°
K
ą
t
α
αα
α
tn
wzgl
ę
dem
osi x
Obliczenia
:
Wyniki
oblicze
ń
:
o
o
o
o
70
t
=
+
=
+
α
=
45
25
45
1
α
αα
α
Ekstremalnych
napr
ęż
e
ń
stycznych
nale
ż
y spodziewa
ć
si
ę
w kierunkach okre
ś
lonych
wzgl
ę
dem osi x przez k
ą
t
α
αα
α
t
równy ok. 70° oraz przez ka
ż
dy k
ą
t wi
ę
kszy lub mniejszy
od
α
αα
α
t
o krotno
ść
90°.
Poniewa
ż
dla stanu napr
ęż
e
ń
z przyk-
ładu 1
α
αα
α
1
= 25°, to dla
α
αα
α
t
ma warto
ść
:
6
11
Ć
wiczenie T4 - Przykład nr 1
Krok 3 –
Obliczenia
i
wpisanie
wyników
oblicze
ń
do
tablicy
tych wyników
Cz
ęść
6 – Obliczenia
napr
ęż
e
ń
stycznych
w kierunkach
α
αα
α
t
+n·45°
wzgl
ę
dem osi x
płaskiego stanu napr
ęż
e
ń
:
σσσσ
x
= 150 MPa,
σσσσ
y
= -250 MPa,
ττττ
xy
= -240 MPa
Nale
ż
y
obliczy
ć
:
Wzory
do oblicze
ń
i obliczenia
:
ττττ
E135
ττττ
E90
ττττ
E45
ττττ
E
ττττ
E-45
Warto
ś
ci
napr
ęż
e
ń
stycznych MPa
?
?
?
?
?
(
)
(
)
(
)
(
)
(
)
0
MPa
312,4
0
MPa
312,4
0
E135
E90
E45
E
45
-
E
=
⋅
=
+
⋅
⋅
=
−
=
⋅
=
+
⋅
⋅
=
=
⋅
=
+
⋅
⋅
=
=
−
−
=
⋅
⋅
−
=
=
⋅
=
−
⋅
⋅
=
τ
τ
τ
τ
o
o
o
o
o
o
o
o
o
o
o
o
o
sin360
312,4
135
45
2
sin
sin270
312,4
90
45
2
sin
sin180
312,4
45
45
2
sin
90
sin
2
4
,
362
4
,
262
45
2
sin
2
σ
σ
sin0
312,4
45
45
2
sin
E
E
E
3
1
E
ττττ
ττττ
ττττ
ττττ
ττττ
12
Ć
wiczenie T4 - Przykład nr 1
Krok 3 –
Obliczenia
i
wpisanie
wyników
oblicze
ń
do
tablicy
tych wyników
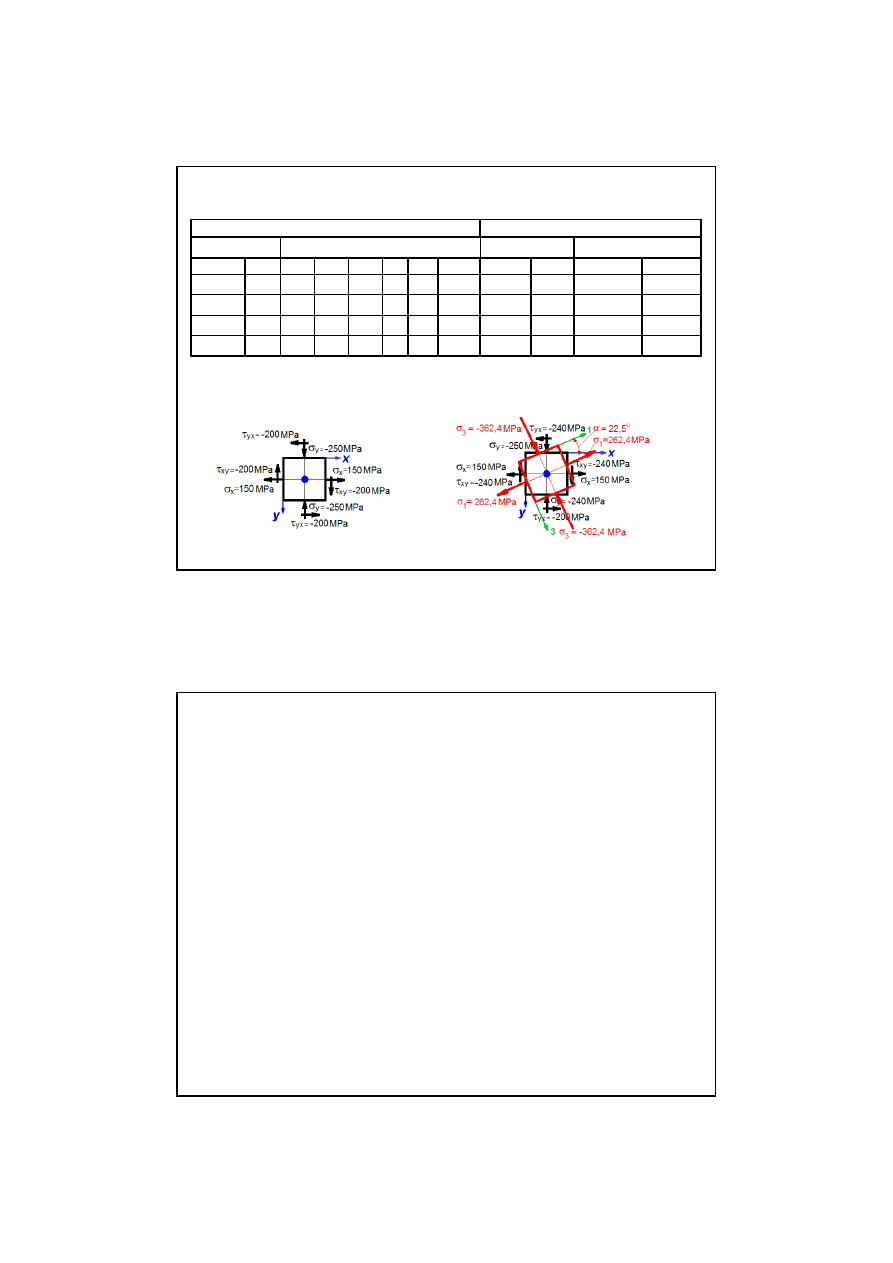
Cz
ęść
7 –Tablica wyników
oblicze
ń
ekstremalnych
napr
ęż
e
ń
rozci
ą
gaj
ą
cych
,
ś
ciskaj
ą
cych
i
stycznych
dla płaskiego stanu napr
ęż
e
ń
o parametrach
σσσσ
x
= 150 MPa,
σσσσ
y
=
-250 MPa,
ττττ
xy
= -240 MPa.
3. Maksymalne
napr
ęż
enie
rozci
ą
gaj
ą
ce
jest wi
ę
ksze od napr
ęż
enia
σσσσ
x
o ok. 75 %, ekstremal-
ne
napr
ęż
enie
ś
ciskaj
ą
ce
przekracza napr
ęż
enie
σσσσ
y
o ok. 45%, a ekstremalne
napr
ęż
enie
styczne
przekracza napr
ęż
enie
ττττ
xy
o ok. 30%.
1. Ekstremalne
napr
ęż
enia
rozci
ą
gaj
ą
ce
i
ś
ciskaj
ą
ce
działaj
ą
w kierunkach głównych okre
ś
lo-
nych wzgl
ę
dem osi
x
przez k
ą
t
α
αα
α
1n
= 25° ± n ·90°, dla których
napr
ęż
enia
styczne
s
ą
zerowe
.
Wnioski wynikaj
ą
ce z tablicy wyników dla przykładu 1
-362,4
-50,0
-362,4
-50,0
-362,4
σσσσ
3180
σσσσ
3135
σσσσ
390
σσσσ
345
σσσσ
3
0
ττττ
E135
205°
α
αα
α
t
+ 135°
0000
σσσσ
2180
262,4
σσσσ
1180
205°
α
αα
α
1
+ 180°
-312,4
ττττ
E90
160°
α
αα
α
t +
90°
0000
σσσσ
2135
-50
σσσσ
1135
160°
α
αα
α
1
+ 135°
0
ττττ
E45
115°
α
αα
α
t
+ 45°
0000
σσσσ
290
262,4
σσσσ
190
115°
α
αα
α
1
+ 90°
312,4
ττττ
E
70°
α
αα
α
t
0000
σσσσ
245
-50,0
σσσσ
145
70°
α
αα
α
1
+ 45°
0
ττττ
E-45
25°
α
αα
α
t
- 45°
0000
σσσσ
2
262,4
σσσσ
1
25°
α
αα
α
1
Warto
ś
ci napr
ęż
e
ń
, MPa
K
ą
t
α
αα
α
tn
Warto
ś
ci napr
ęż
e
ń
, MPa
K
ą
t
α
αα
α
1n
Parametry ekstr. napr
ęż
e
ń
stycznych
Parametry napr
ęż
e
ń
głównych
2. Ekstremalne
napr
ęż
enia
styczne
wyst
ę
puj
ą
w kierunkach okre
ś
lonym wzgl
ę
dem osi
x
przez
k
ą
t
α
αα
α
tn
= 70°± n ·90°
,
dla których
napr
ęż
enia
styczne
s
ą
ró
ż
ne
od
zera
.
7
13
Ć
wiczenie T4 - Przykład nr 1
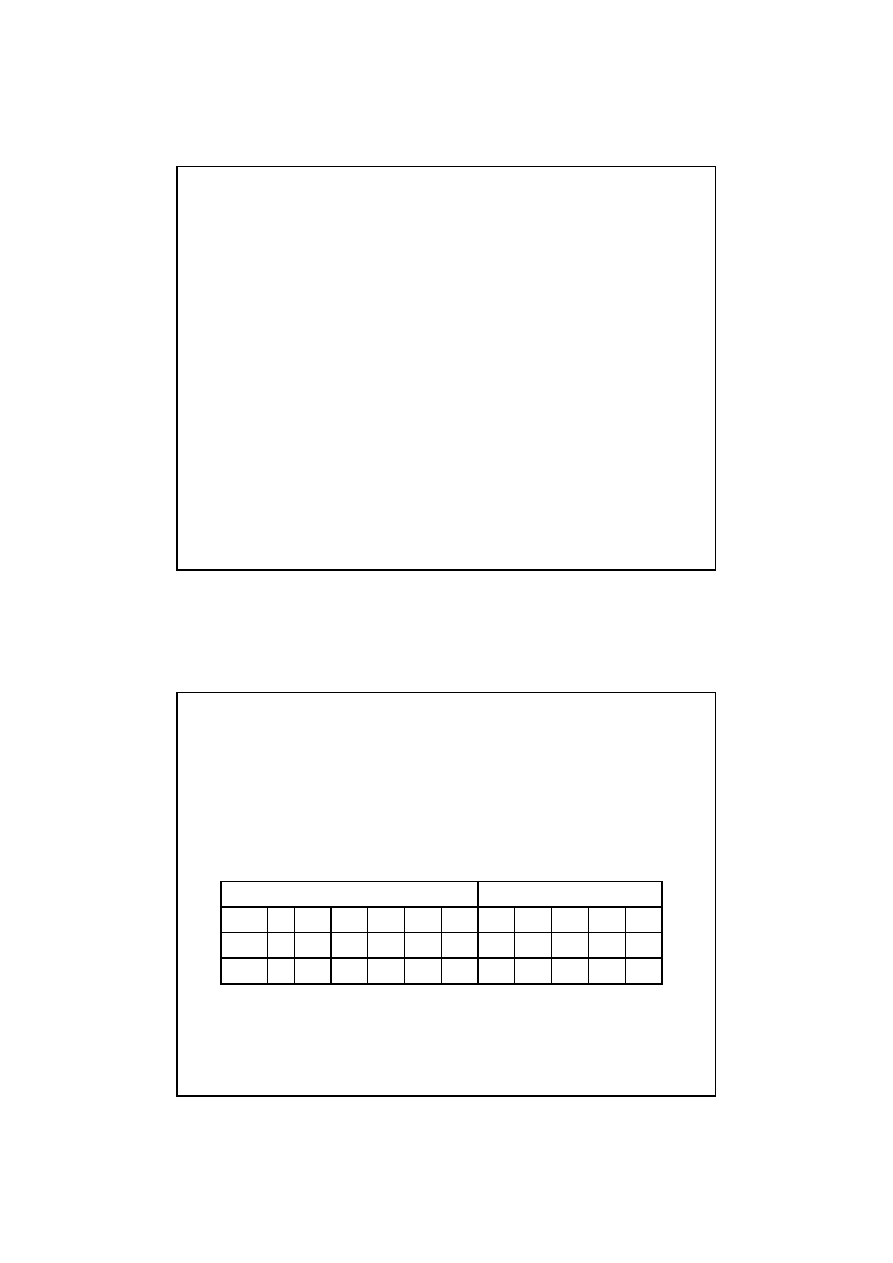
Krok 4 –
Ilustracja
warto
ś
ci
i
kierunków
napr
ęż
e
ń
głównych za pomoc
ą
schematu
EPT
.
Schemat
EPT
dla
zadanego
stanu
napr
ęż
e
ń
o parametrach
wyra
ż
onych
w postaci ogólnej
Schemat
EPT
dla
warto
ś
ci
i
kierunków
napr
ęż
e
ń
głównych obliczonych
dla
zadanego
stanu napr
ęż
e
ń
0
ττττ
E135
205°
α
αα
α
t
+ 135°
-362,4
σσσσ
3180
0000
σσσσ
2180
262,4
σσσσ
1180
205°
α
αα
α
1
+ 180°
-312,4
ττττ
E90
160°
α
αα
α
t +
90°
-50,0
σσσσ
3135
0000
σσσσ
2135
-50
σσσσ
1135
160°
α
αα
α
1
+ 135°
0
ττττ
E45
115°
α
αα
α
t
+ 45°
-362,4
σσσσ
390
0000
σσσσ
290
262,4
σσσσ
190
115°
α
αα
α
1
+ 90°
312,4
ττττ
E
70°
α
αα
α
t
-50,0
σσσσ
345
0000
σσσσ
245
-50,0
σσσσ
145
70°
α
αα
α
1
+ 45°
0
ττττ
E-45
25°
α
αα
α
t
- 45°
-362,4
σσσσ
3
0000
σσσσ
2
262,4
σσσσ
1
25°
α
αα
α
1
Warto
ś
ci napr
ęż
e
ń
, MPa
K
ą
t
α
αα
α
tn
Warto
ś
ci napr
ęż
e
ń
, MPa
K
ą
t
α
αα
α
1n
Parametry ekstr. napr
ęż
e
ń
stycznych
Parametry napr
ęż
e
ń
głównych
Ć
wiczenie T4 - Przykład nr 2
Temat:
Dla
płaskiego stanu
napr
ęż
e
ń
, który analizowano w przykładzie 1, obliczy
ć
– za pomoc
ą
uogólnionego prawa Hooke’a –
parametry
stanu odkształce
ń
głów-
nych
w punkcie obj
ę
to
ś
ci materiału spr
ęż
ysto-plastycznego o parametrach:
E = 0,7·10
5
MPa,
νννν
= 0,2, R
0,05
= 370 MPa, R
0,2
= 450 MPa,
oraz okre
ś
li
ć
graniczne warto
ś
ci
σσσσ
1g
i
σσσσ
3g
napr
ęż
e
ń
głównych
, które w tym mate-
riale
nie
powinny by
ć
przekroczone
, aby wykonane obliczenia były dokładne.
Nowe
poj
ę
cia dotycz
ą
ce
tematu
zadania
:
1. Uogólnione prawo Hooke’a dla odkształce
ń
obj
ę
to
ś
ciowych
(głównych) oraz
odkształce
ń
postaciowych
w punkcie obj
ę
to
ś
ci materiału.
2. Główne ró
ż
nice fizyczne pomi
ę
dzy odkształceniami
obj
ę
to
ś
ciowymi
a odksz-
tałceniami
postaciowymi
w punkcie objetosci materiału.
3. Nazwy i definicje fizyczne parametrów
spr
ęż
ysto
ś
ci
E,G,
νννν
dla materiałów kons-
trukcyjnych.
4. Nazwy i definicje fizyczne parametrów
wytrzymało
ś
ci
R
H
, R
0,05
, R
e
, R
0,2
, R
m
, R
c
,
R
r
dla materiałów
spr
ęż
ysto
-
plastycznych
i
spr
ęż
ysto
-
kruchych
.
14
8
Ć
wiczenie T4 - Przykład nr 2
Temat:
Dla
płaskiego stanu
napr
ęż
e
ń
, który analizowano w przykładzie 1, obliczy
ć
– za pomoc
ą
uogólnionego prawa Hooke’a – parametry stanu
odkształce
ń
głów-
nych
w punkcie obj
ę
to
ś
ci materiału spr
ęż
ysto-plastycznego o parametrach:
E = 0,7·10
5
MPa,
νννν
= 0,2, R
0,05
= 350 MPa, R
0,2
= 450 MPa,
oraz okre
ś
li
ć
graniczne warto
ś
ci
σσσσ
1g
i
σσσσ
3g
napr
ęż
e
ń
głównych
, które w tym mate-
riale
nie
powinny by
ć
przekroczone
, aby wykonane obliczenia były dokładne.
Kroki obliczeniowe:
1.Tablica
danych
i szablon tablicy
wyników
oblicze
ń
.
2. Obliczenie parametrów stanu
odkształce
ń
głównych
.
3. Okre
ś
lenie granicznych warto
ś
ci
σσσσ
1g
i
σσσσ
3g
napr
ęż
e
ń
głównych
.
4
.
Sformułowanie
wniosków
wynikaj
ą
cych z tablicy
wyników
oblicze
ń
.
15
Ć
wiczenie T4 - Przykład nr 2
Temat:
Dla
płaskiego stanu
napr
ęż
e
ń
, który analizowano w przykładzie 1, obliczy
ć
– za po-
moc
ą
uogólnionego prawa Hooke’a – parametry stanu
odkształce
ń
głównych
w punkcie
obj
ę
to
ś
ci materiału spr
ęż
ysto-plastycznego o parametrach
:
E = 0,7·10
5
MPa,
νννν
= 0,2, R
0,05
= 370 MPa, R
0,2
= 450 MPa
,
oraz okre
ś
li
ć
graniczne warto
ś
ci
σσσσ
1g
i
σσσσ
3g
napr
ęż
e
ń
głównych
, które w tym materiale
nie
po-
winny by
ć
przekroczone
, aby wykonane obliczenia były dokładne
.
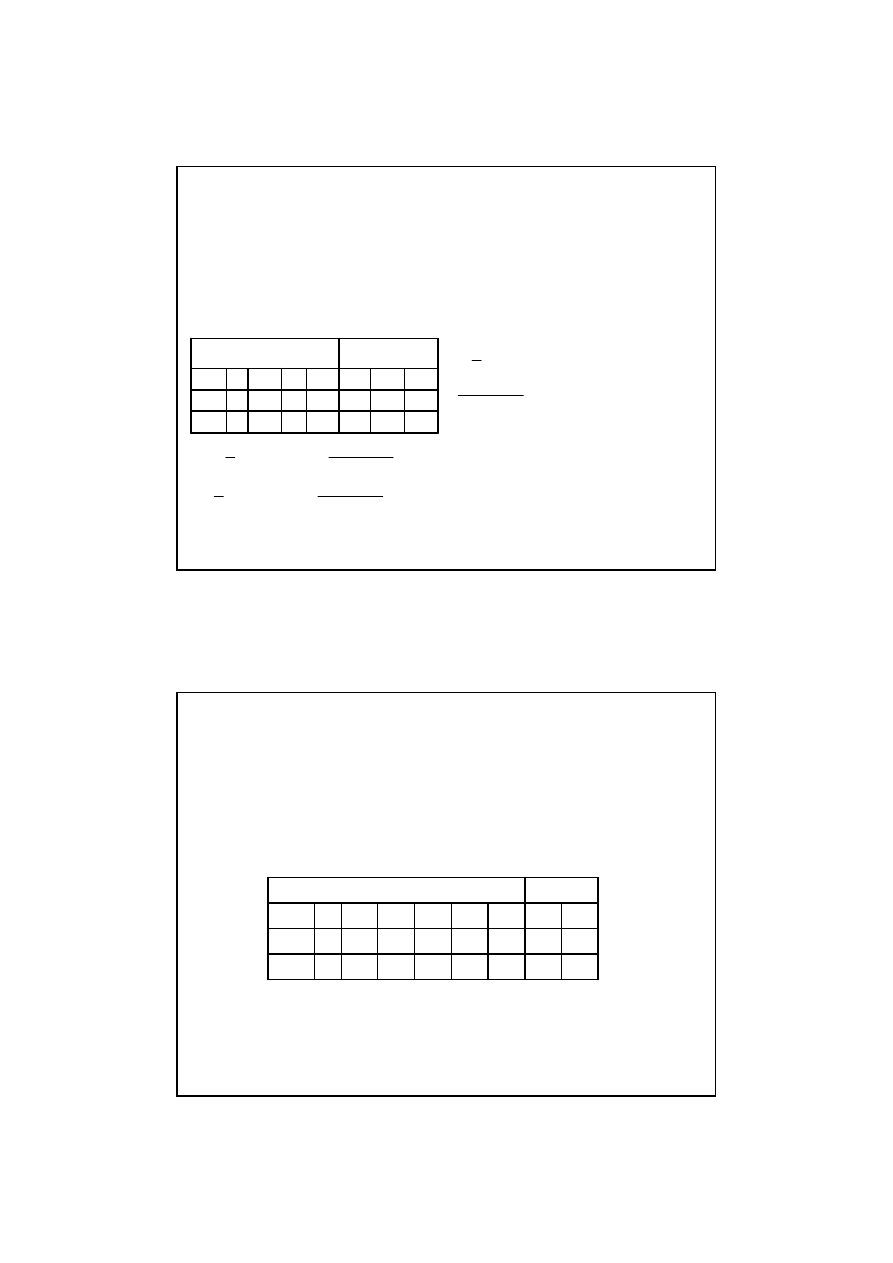
Krok 1.Tablica
danych
i szablon tablicy
wyników
oblicze
ń
16
Wyniki oblicze
ń
?
?
?
?
?
-362,4
0
262,4
450
350
0,2
0,7·10
5
MPa
MPa
promil
promil
promil
MPa
MPa
MPa
MPa
MPa
÷
MPa
σσσσ
2g
σσσσ
1g
εεεε
3
εεεε
2
εεεε
1
σσσσ
3
σσσσ
2
σσσσ
1
R
0,2
R
0,05
νννν
E
Dane do oblicze
ń
9
Ć
wiczenie T4 - Przykład nr 2
Temat:
Dla
płaskiego stanu
napr
ęż
e
ń
, który analizowano w przykładzie 1, obliczy
ć
– za po-
moc
ą
uogólnionego prawa Hooke’a – parametry stanu
odkształce
ń
głównych
w punkcie
obj
ę
to
ś
ci materiału spr
ęż
ysto-plastycznego o parametrach
:
E = 0,7·10
5
MPa,
νννν
= 0,2, R
0,05
=
370 MPa, R
0,2
= 450 MPa
,
oraz okre
ś
li
ć
graniczne warto
ś
ci
σσσσ
1g
i
σσσσ
3g
napr
ęż
e
ń
głównych
, któ-
re w tym materiale
nie
powinny by
ć
przekroczone
, aby wykonane obliczenia były dokładne
.
Krok 2. Obliczenie parametrów stanu
odkształce
ń
głównych
17
Nale
ż
y
obliczy
ć
:
Wzory
do oblicze
ń
i obliczenia:
?
?
?
-362,4
0
262,4
0,2
0,7·10
5
promil
promil
promil
MPa
MPa
MPa
÷
MPa
εεεε
3
εεεε
2
εεεε
1
σσσσ
3
σσσσ
2
σσσσ
1
νννν
E
Parametry stanu
odkształce
ń
Dane do oblicze
ń
3
1
10
4,8
−
−
⋅
=
⋅
=
⋅
−
⋅
−
⋅
⋅
⋅
=
=
σ
+
σ
ν
−
σ
=
5
6
6
6
5
3
2
1
10
4
,
478
)]
10
4
,
362
0
(
2
,
0
10
4
,
262
[
10
10
7
,
0
1
)]
(
[
E
1
εεεε
5
2
10
0,3
−
−
⋅
=
⋅
=
⋅
−
⋅
⋅
−
⋅
⋅
=
σ
+
σ
ν
−
σ
=
5
6
6
6
5
3
1
2
10
6
,
28
)]
10
4
,
362
10
4
,
262
(
2
,
0
0
[
10
10
7
,
0
1
)]
(
[
E
1
εεεε
3
3
10
5,9
−
−
⋅
−
=
⋅
−
=
+
⋅
⋅
−
⋅
−
⋅
⋅
=
σ
+
σ
ν
−
σ
=
5
6
6
6
5
2
1
3
10
7
,
592
)]
0
10
4
,
262
(
2
,
0
10
4
,
362
[
10
10
7
,
0
)]
(
[
1
E
1
εεεε
Ć
wiczenie T4 - Przykład nr 2
Temat:
Dla
płaskiego stanu
napr
ęż
e
ń
, który analizowano w przykładzie 1, obliczy
ć
– za po-
moc
ą
uogólnionego prawa Hooke’a – parametry stanu
odkształce
ń
głównych
w punkcie
obj
ę
to
ś
ci materiału spr
ęż
ysto-plastycznego o parametrach
:
E = 0,7·10
5
MPa,
νννν
= 0,2, R
0,05
=
370 MPa, R
0,2
= 450 MPa
,
oraz okre
ś
li
ć
graniczne warto
ś
ci
σσσσ
1g
i
σσσσ
3g
napr
ęż
e
ń
głównych
, któ-
re w tym materiale
nie
powinny by
ć
przekroczone
, aby wykonane obliczenia były dokładne
.
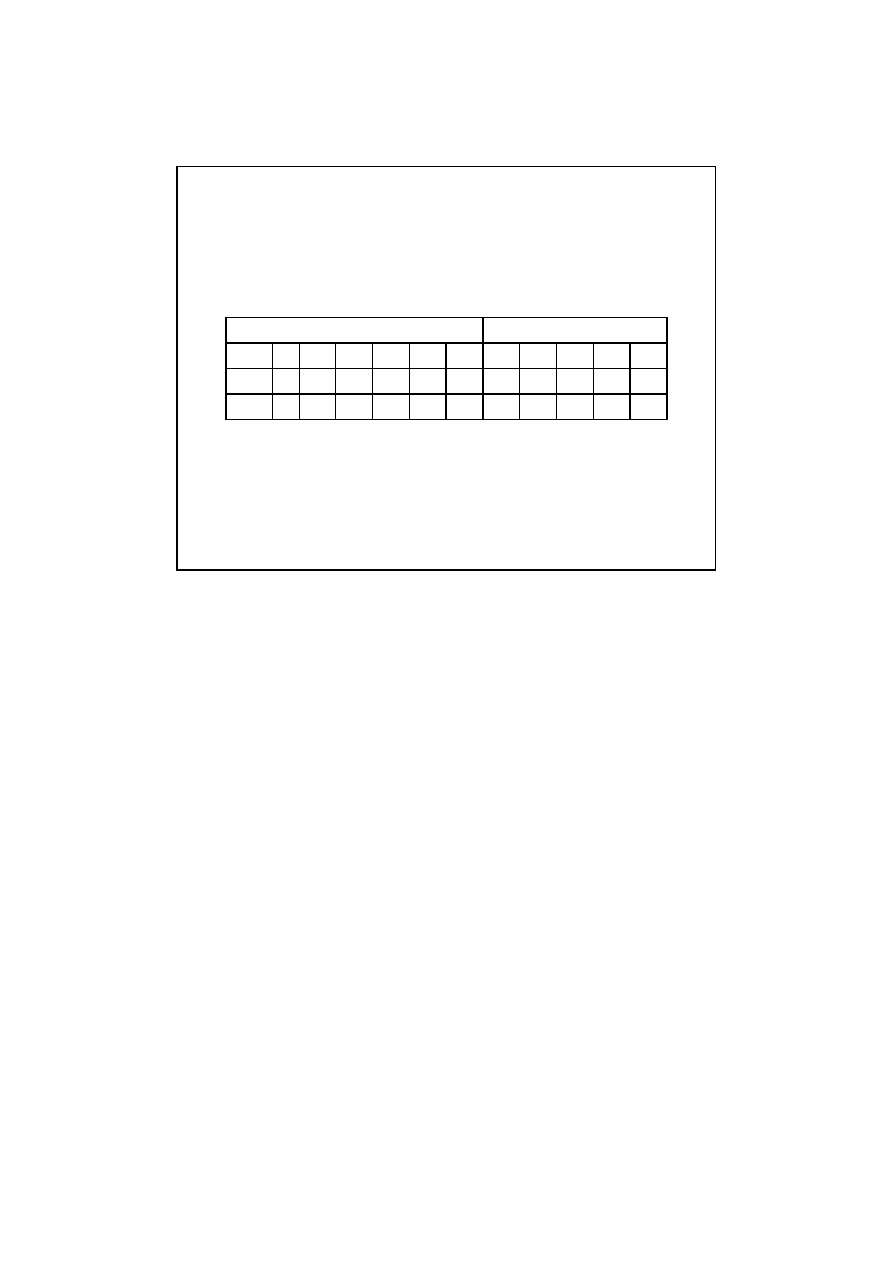
Krok 3. Okre
ś
lenie granicznych warto
ś
ci
σσσσ
1g
i
σσσσ
3g
napr
ęż
e
ń
głównych
18
Nale
ż
y
okre
ś
li
ć
:
Zasada okre
ś
lania napr
ęż
e
ń
σσσσ
1g
i
σσσσ
3g
:
?
?
-362,4
0
262,4
450
350
0,2
0,7·10
5
MPa
MPa
MPa
MPa
MPa
MPa
MPa
÷
MPa
σσσσ
2g
σσσσ
1g
σσσσ
3
σσσσ
2
σσσσ
1
R
0,2
R
0,05
νννν
E
Wyniki
Dane do oblicze
ń
Uogólnione
prawo
Hooke’a
daje wyniki
zgodne
z
rzeczywisto
ś
ci
ą
wtedy
,
gdy
najwi
ę
ksza warto
ść
bezwzgl
ę
dna
napr
ęż
enia
głównego
w analizowanej
obj
ę
to
ś
ci
materiału
nie
jest
wi
ę
ksza
od
granicy
proporcjonalno
ś
ci
tego materiału.
10
Ć
wiczenie T4 - Przykład nr 2
Temat:
Dla
płaskiego stanu
napr
ęż
e
ń
, który analizowano w przykładzie 1, obliczy
ć
– za po-
moc
ą
uogólnionego prawa Hooke’a – parametry stanu
odkształce
ń
głównych
w punkcie
obj
ę
to
ś
ci materiału spr
ęż
ysto-plastycznego o parametrach
:
E = 0,7·10
5
MPa,
νννν
= 0,2, R
0,05
=
370 MPa, R
0,2
= 450 MPa
,
oraz okre
ś
li
ć
graniczne warto
ś
ci
σσσσ
1g
i
σσσσ
3g
napr
ęż
e
ń
głównych
, któ-
re w tym materiale
nie
powinny by
ć
przekroczone
, aby wykonane obliczenia były dokładne
.
Krok 4. Sformułowanie
wniosków
wynikaj
ą
cych z tablicy
wyników
oblicze
ń
19
-370
370
-5,9
0,3
4,8
-362,4
0
262,4
450
350
0,2
0,7·10
5
MPa
MPa
promil
promil
promil
MPa
MPa
MPa
MPa
MPa
÷
MPa
σσσσ
2g
σσσσ
1g
εεεε
3
εεεε
2
εεεε
1
σσσσ
3
σσσσ
2
σσσσ
1
R
0,2
R
0,05
νννν
E
Wyniki oblicze
ń
Dane do oblicze
ń
Wnioski
wynikaj
ą
ce z tablicy
wyników
oblicze
ń
dla przykładu 2
1. Ka
ż
dy z parametrów
εεεε
1
,
εεεε
2
,
εεεε
3
stanu
odkształce
ń
głównych
obliczony dla
płaskiego
stanu
napr
ęż
e
ń
jest ró
ż
ny od zera, co wskazuje,
ż
e
płaski
stan
napr
ęż
e
ń
powoduje w punkcie
obj
ę
to
ś
ci materiału
przestrzenny
stan
odkształce
ń
.
2. Gdy
napr
ęż
enie
główne
jest
dodatnie
(rozci
ą
gaj
ą
ce), to boki elementarnego prostopadło
ś
-
cianu
EPN
zgodne z kierunkiem tego napr
ęż
enia ul
ę
gaj
ą
wydłu
ż
eniu
, gdy jest
ujemne
–
ulegaj
ą
skróceniu
.