1
7.1.4. Przekroje podwójnie zbrojone
Zazwyczaj najpierw zakłada się wymiary przekroju, a następnie oblicza się zbrojenie.
Im wyższy przekrój tym mniej potrzeba zbrojenia
, ale oczywiście tym więcej betonu i
tym mniej w pełni użytecznej przestrzeni pod belkami. Zagadnienie ekonomicznego
zbrojenia było przedmiotem analiz prawie od początków stosowania żelbetu. Takie
analizy można opierać np. na
minimalizacji sumy kosztów betonu i zbrojenia
. Poważne
znaczenie mogą mieć jednak różne inne czynniki (np. walory użytkowe, sztywność
elementu i konstrukcji, potrzeba dopasowania projektowanego elementu do innych itp.);
niektóre z nich trudno jednoznacznie ująć ilościowo. Dlatego zwykle wymiary
przekrojów dobiera się tak, aby uzyskać „zgrabne” rozwiązanie, dostosowane do
wymagań rozpatrywanego projektu, przy którym µ< µ
lim
(dla µ> µ
lim
otrzymuje się
bardzo duże zbrojenie, patrz Wykres 1, część 2), a ugięcia nie przekraczają wartości
granicznych. Wstępne wskazówki dotyczące stosunku wysokości użytecznej przekroju
do rozpiętości można uzyskać na podstawie tablicy zawartej w rozdziale dotyczącym
ugięć.
Tak więc, na ogół stosuje się wymiary przekroju na tyle duże, żeby zbrojenie
ściskane nie było potrzebne.
2
Najczęściej w praktyce występuje następujące zagadnienie. Potrzebna jest
nośność większa niż M
lim
(M
lim
oznacza tu moment graniczny osiągany dla
ξ = ξ
lim
). Np. projektując zbrojenie przekroju na moment M
Ed
stwierdzono, że
M
Ed
> M
lim
, a zbrojenie potrzebne do osiągnięcia tego momentu w przekroju bez
zbrojenia ściskanego jest bardzo duże. Jeżeli nie chcemy zwiększać przekroju, to
trzeba zastosować ściskane zbrojenie o polu A
s2
.
Poszukujemy rozwiązania przy x = x
lim
.
Każde zadanie dotyczące nośności można rozwiązać na podstawie warunków
równowagi i założenia płaskich przekrojów. Powszechnie stosowany prosty
sposób polega na przedstawieniu granicznego momentu zginającego w postaci
sumy dwóch par sił.
Wyjątkiem mogą być przypadki, w których występują lokalnie słabsze obszary
np. zmniejszenia wysokości użytecznej ze względu na wycięcia lub otwory.
Takie obszary można wzmocnić stosując zbrojenie ściskane.
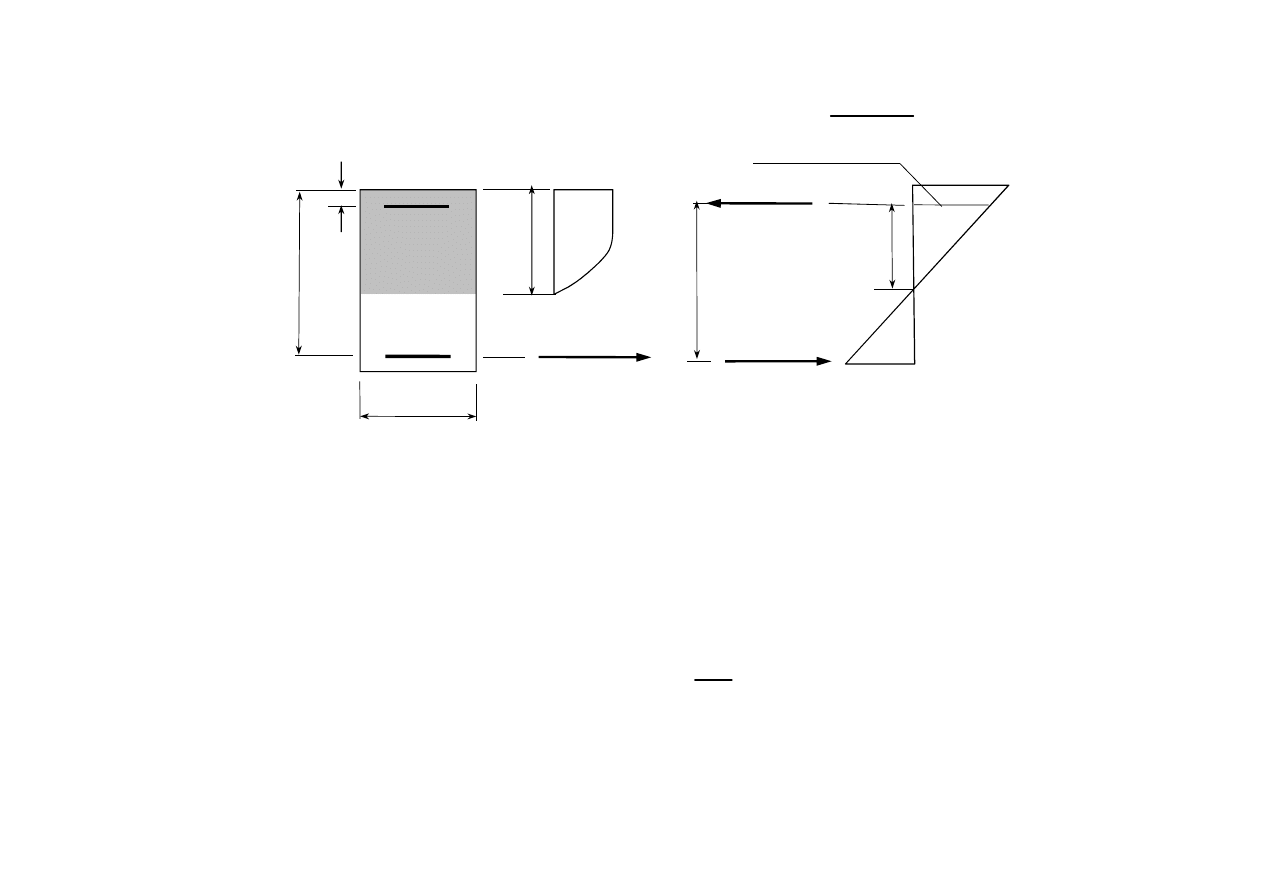
3
Para 1 składa się z siły ściskającej w betonie (wyznaczonej dla x = x
lim
) i równoważącej
ją siły w zbrojeniu rozciąganym. Do wytworzenia momentu M
lim
potrzebne jest zbrojenie
rozciągane o polu przekroju A
s1,lim
yd
cd
s
f
f
d
b
A
lim
,
1
lim
,
1
α
=
Współczynnik α
1,lim
można wziąć z tablic albo z wykresu.
Rys. 7.1.4. Siły wewnętrzne w przekroju podwójnie zbrojonym
lim
2
lim
2
2
x
a
x
cu
s
−
=
ε
ε
ε
cu2
a
2
x
lim
f
cd
b
A
s1
Para sił 1
(M
lim
)
A
s2
A
s2
σ
s2
∆A
s1
f
yd
A
s1,lim
f
yd
Para sił 2
(M
2
)
d-a
2
x
lim
- a
2
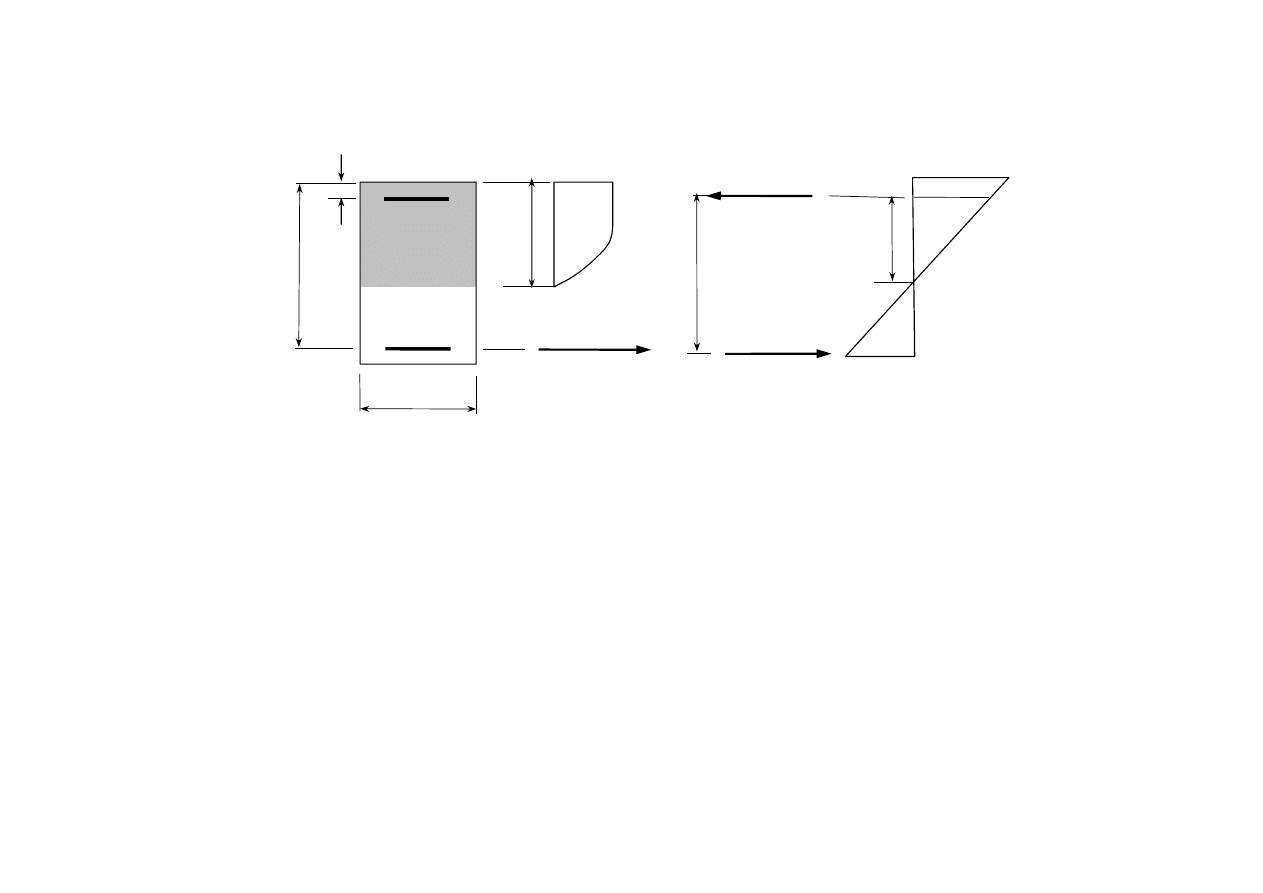
4
Para 2 składa się z dwóch równych sił: A
s2
σ
s2
i ∆A
s1
f
yd
Zwykle odkształcenie w zbrojeniu ściskanym jest na tyle duże, że σ
s2
= f
yd
, a więc nie
trzeba obliczać wartości σ
s2
i ∆A
s1
= A
s2
.
.
Wyjątkowo, w przekrojach, które mają małą
wysokość (np. niezbyt grube płyty), wartość a
2
może być duża w porównaniu do x
lim
– wtedy naprężenie w zbrojeniu ściskanym może być mniejsze od obliczeniowej
granicy plastyczności.
ε
cu2
a
2
x
lim
f
cd
b
A
s1
Para sił 1
(M
lim
)
A
s2
A
s2
σ
s2
∆A
s1
f
yd
A
s1,lim
f
yd
Para sił 2
(M
2
)
d-a
2
x
lim
- a
2
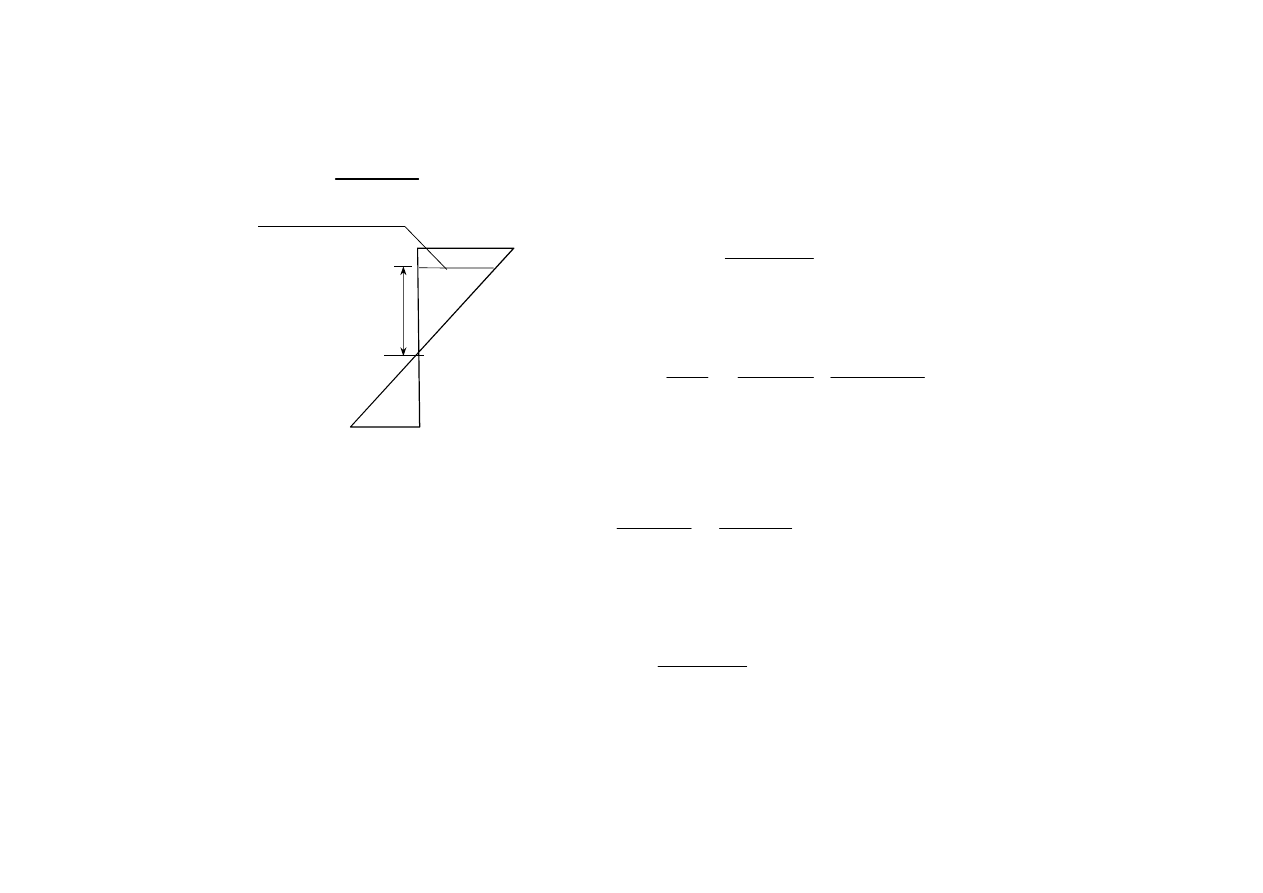
5
−
=
=
lim
2
lim
2
2
2
ξ
δ
ξ
ε
σ
yd
cu
s
yd
s
f
E
f
k
lim
lim
2
1
ξ
ξ
ε
−
=
yd
cu
s
f
E
lim
2
lim
2
1
ξ
δ
ξ
−
−
=
k
x
lim
- a
2
ε
cu2
lim
2
lim
2
2
x
a
x
cu
s
−
=
ε
ε
Z zależności
wynika, że
−
=
lim
2
lim
2
2
x
a
x
cu
s
ε
ε
6
Moment tej pary sił wynosi
(
)
2
2
2
2
a
d
A
M
s
s
−
=
σ
lim
2
M
M
M
Ed
−
=
Zbrojenie potrzebne ze względu na ten moment
(
)
2
2
lim
2
a
d
M
M
A
s
Ed
s
−
−
=
σ
Ostatecznie wymagane pole zbrojenia ściskanego wynosi A
s2
a pole zbrojenia
rozciąganego
1
lim
,
1
1
s
s
s
A
A
A
∆
+
=
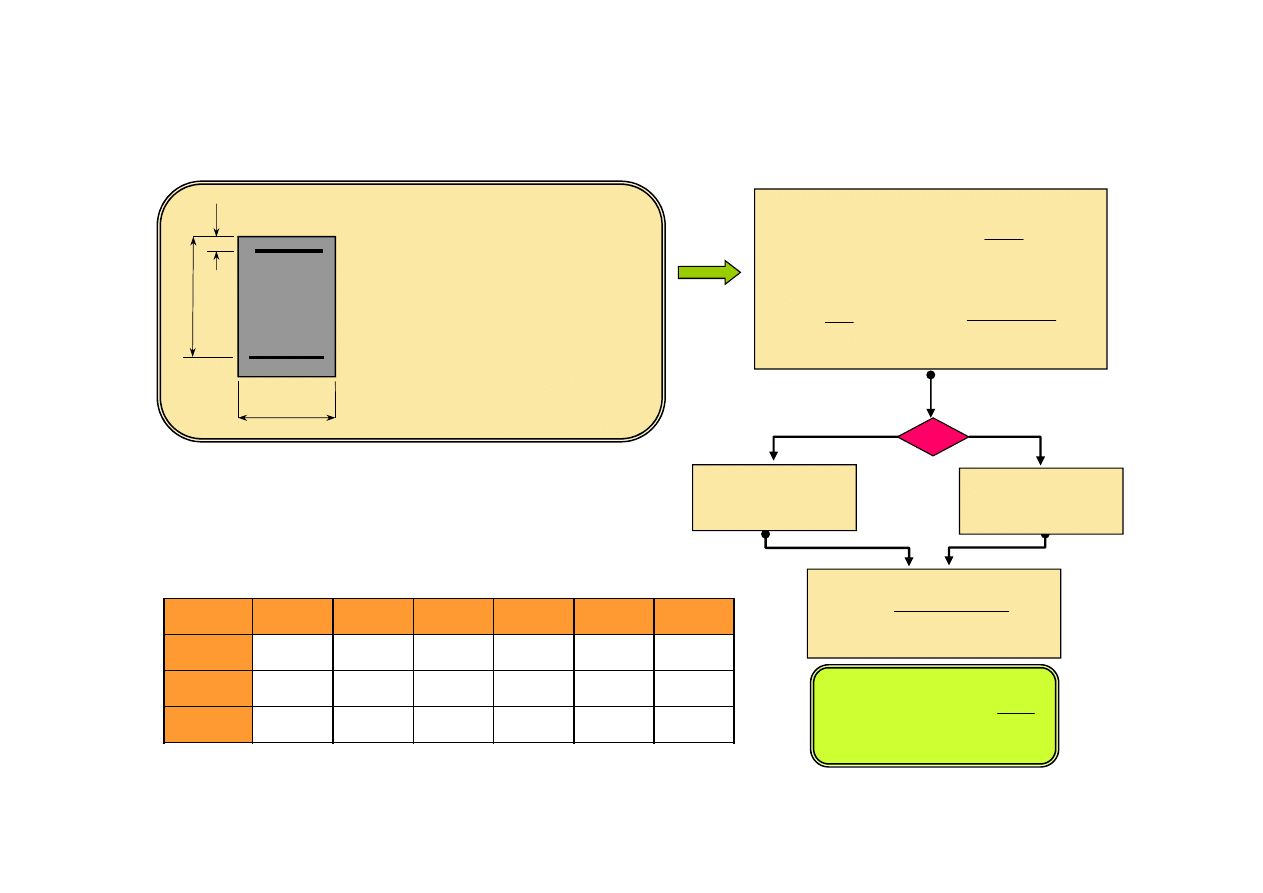
Wzory wyprowadzone w tym punkcie przedstawiono jako algorytm w tab. 4.
Druga para sił ma przenieść nadwyżkę momentu
Łatwo jest zbudować podobne algorytmy dla betonów mocniejszych wykorzystując
dane z tablicy 2.
yd
s
s
s
f
A
A
2
2
1
σ
=
∆
7
Tab. 4. Obliczanie zbrojenia przekrojów podwójne zbrojonych - beton f
ck
≤ 50 MPa
yd
cd
s
f
f
d
b
A
lim
,
1
lim
,
1
α
=
lim
2
lim
2
1
ξ
δ
ξ
−
−
=
k
1
2
<
k
1
2
≥
k
(
)
2
2
lim
2
a
d
M
M
A
s
Ed
s
−
−
=
σ
yd
s
s
s
s
f
A
A
A
2
2
lim
,
1
1
σ
+
=
Dane: b, d, a
2
f
cd
, f
yd
Oblicza się: A
s1
, A
s2
a
2
b
d
A
s1
A
s2
cd
Ed
f
d
b
M
M
2
lim
lim
µ
=
>
d
a
2
2
=
δ
f
yd
=
190
210
310
350
420
435
ξ
lim
=
0,787
0,769
0,693
0,667
0,625
0,617
µ
lim
=
0,428
0,424
0,399
0,390
0,374
0,371
α
1,lim
=
0,637
0,628
0,561
0,540
0,506
0,499
yd
s
f
k
2
2
=
σ
yd
s
f
=
2
σ
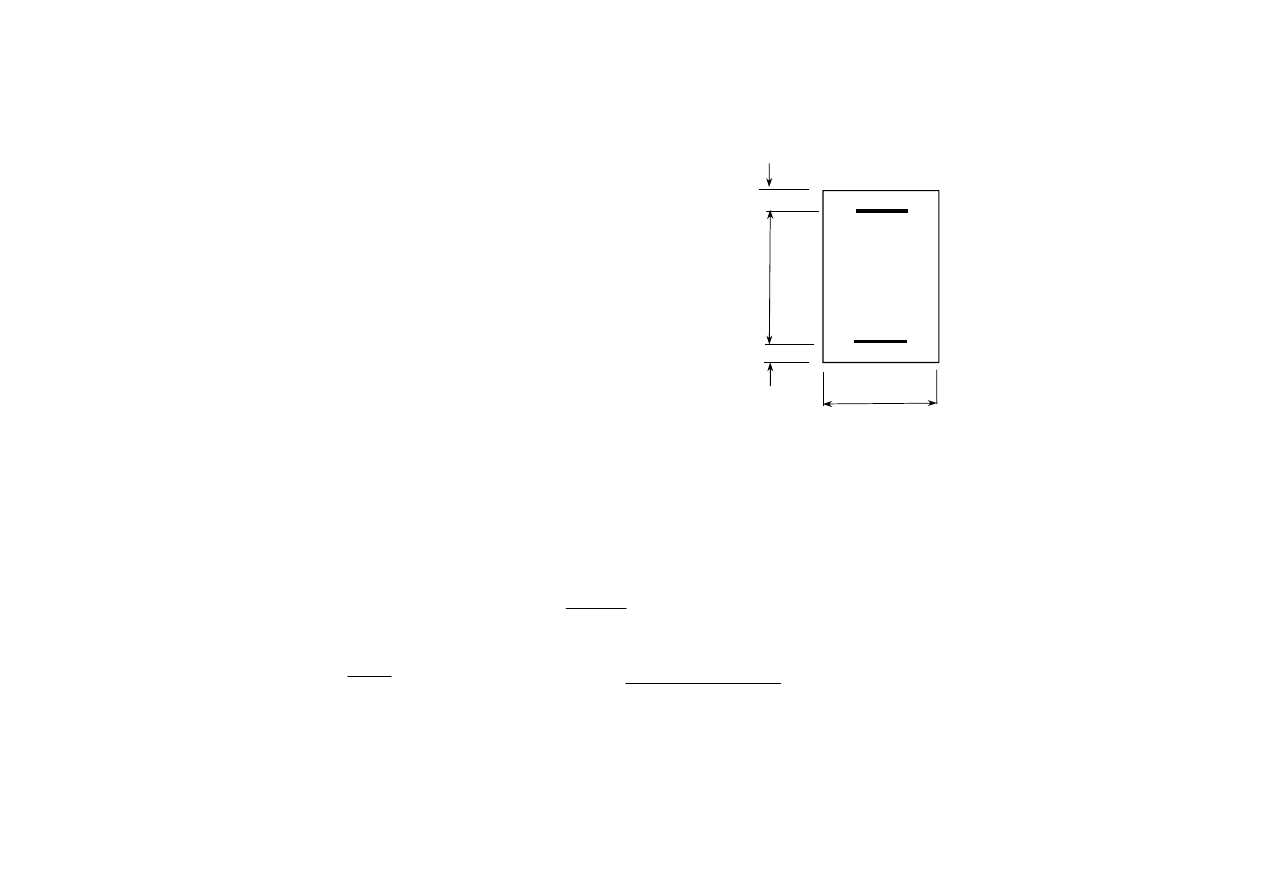
8
Przykład
Przekrój podwójnie zbrojony
Dane: wymiary przekroju,
beton f
ck
= 25 MPa, f
cd
= 17,86 MPa,
stal: f
yd
= 420 MPa ,
moment obliczeniowy: M
Ed
= 450 kNm.
Należy obliczyć A
s1
i A
s2
.
2
4
lim
,
1
cm
04
,
29
10
420
86
,
17
45
,
0
30
,
0
506
,
0
=
⋅
⋅
=
s
A
1111
,
0
450
50
2
=
=
δ
1
37
,
1
625
,
0
1
1111
,
0
625
,
0
2
>
=
−
−
=
k
a więc w zbrojeniu A
s2
osiąga się granicę plastyczności.
50
300
400
50
A
s2
A
s1
Według tab. 4:
MNm
0,450
M
4062
,
0
86
,
17
45
,
0
30
,
0
374
,
0
Ed
2
lim
=
<
=
⋅
⋅
⋅
=
M
Potrzebne jest zbrojenie ściskane
9
Warto porównać ten wynik z poprzednim przykładem. Stosując beton
f
ck
= 25 MPa, trzeba zużyć 2,61+31,65 = 34,26 cm
2
zbrojenia. Ten sam
moment można przenieść stosując 25,99 cm
2
zbrojenia rozciąganego i
beton f
ck
= 80 MPa.
(
)
2
4
2
cm
61
,
2
10
05
,
0
45
,
0
420
4062
,
0
450
,
0
=
−
−
=
s
A
2
1
cm
65
,
31
04
,
29
61
,
2
=
+
=
s
A
10
7.2. Przekroje teowe i inne obliczane jako teowe
7.2.1. Uwagi wstępne
Rozpatruje się przekroje teowe, w których strefa ściskana mieści się w półce,
całkowicie lub częściowo. Np. w belkach ciągłych (z półką u góry), momenty zginające
zwykle są dodatnie w środkach przęseł, a więc przekroje w tych częściach belek można
projektować jako przekroje teowe (półka jest po stronie ściskanej). Przekroje w
częściach przypodporowych, gdzie zwykle rozciągana jest górna część belki a ściskana
dolna, projektuje się jako prostokątne o szerokości równej grubości środnika.
Nośność przekrojów teowych zależy od kształtu strefy ściskanej. Kształt strefy
rozciąganej nie ma wpływu na obliczenia, gdyż zakłada się, że wytrzymałość betonu
na rozciąganie jest zerowa. Dlatego teoria przekrojów teowych znajduje zastosowanie
do innych przekrojów, mających prostokątną strefę ściskaną. Łatwo zauważyć, że
równania dotyczące przekroju teowego są takie same jak równania dotyczące
przekroju skrzynkowego, w którym suma szerokości ścianek jest równa szerokości
środnika w porównywanym teowniku.
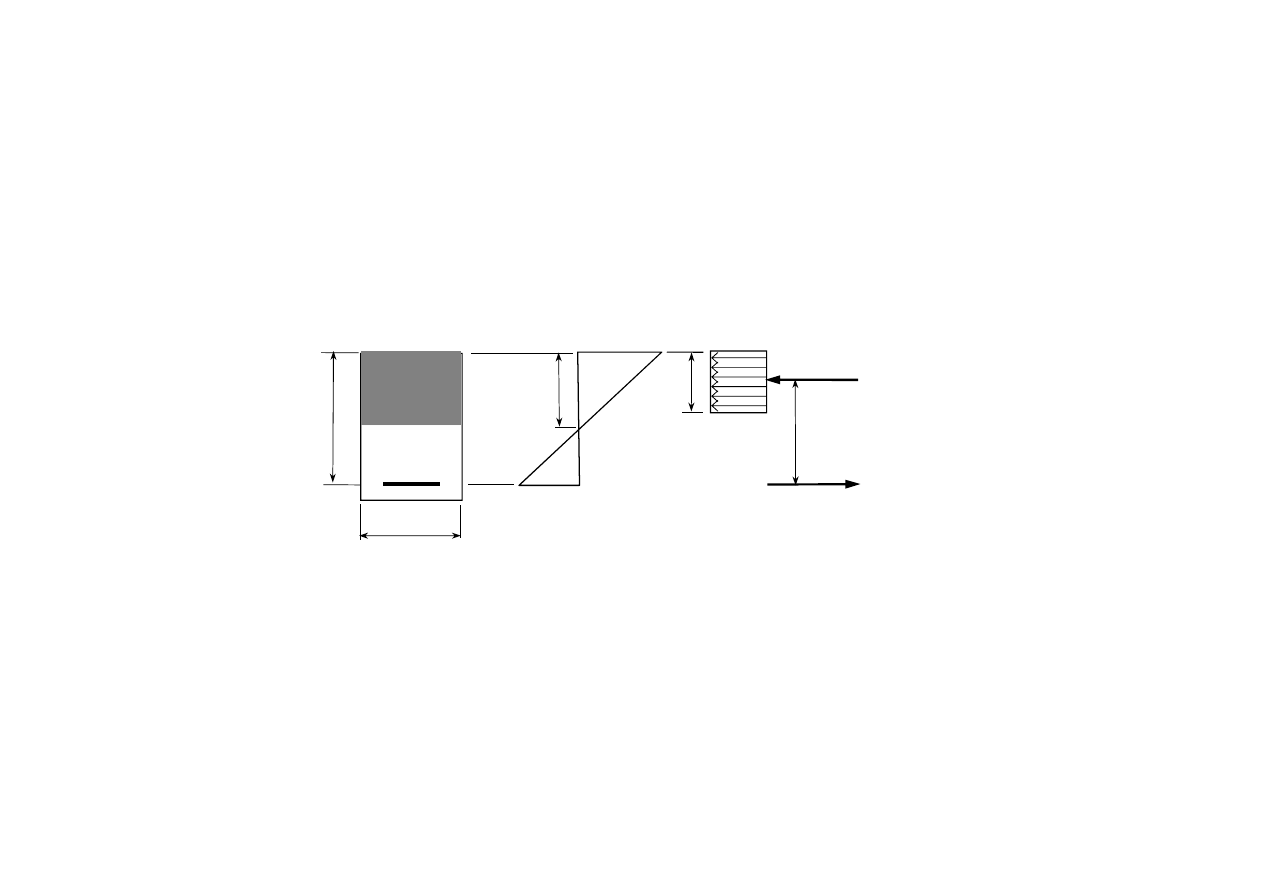
11
W piśmiennictwie, jak np. w [ ] i [], można znaleźć analizy przekrojów teowych
(w przypadku tzw. przekrojów rzeczywiście teowych raczej zawiłe) przy
zastosowaniu paraboliczno-prostokątnego wykresu naprężeń w betonie. Eurokod
zezwala na stosowanie prostokątnego wykresu naprężeń w strefie ściskanej. Takie
założenie bardzo upraszcza obliczenia przekrojów teowych - dlatego na nim
oprzemy metodę przedstawioną w tym wykładzie.
Współczynniki λ i η i inne szczegóły związane ze stosowaniem prostokątnego
wykresu naprężeń przedstawiono w wykładzie dotyczącym założeń Eurokodu.
Równania równowagi mają teraz postać
ηf
cd
ε
cu3
= ε
cu2
d
P
c
b
x
A
s1
λx
A
s1
f
yd
z = d - 0,5λx
yd
s
cd
c
f
A
f
x
b
P
1
=
=
η
λ
(
)
cd
c
Rd
f
x
d
x
b
z
P
M
η
λ
λ
5
,
0
−
=
=
(S)
(M)
12
Powtarzając w dalszym ciągu – przy założeniu, że wykres naprężeń jest
prostokątny - tok postępowania, który doprowadził do uzyskania wzorów
związanych z wykresem paraboliczno- prostokątnym, można uzyskać wzory
podobne do umieszczonych w tablicach 1 i 2. Jednakże w przekrojach teowych
przekroczenie ξ
lim
jest prawie niemożliwe, gdyż strefa ściskana jest zwykle
znacznie szersza od żebra i równowagę sił uzyskuje się przy umiarkowanym
zasięgu naprężeń ściskających. Dlatego wzorów, które są właściwe dla ξ > ξ
lim
nie
będzie się tu zamieszczać.
Dzieląc obie strony równania (S) przez bdf
cd
, a obie strony (M) przez bd
2
f
cd
otrzymuje się:
yd
s
cd
c
f
A
f
x
b
P
1
=
=
η
λ
(
)
cd
c
Rd
f
x
d
x
b
z
P
M
η
λ
λ
5
,
0
−
=
=
1
α
ληξ
ω
=
=
(
)
λξ
ληξ
µ
µ
5
,
0
1 −
=
=
Rd
(S)
(M)
Wyznaczając ξ z równania kwadratowego (M) i podstawiając do tego rozwiązania
wynikający z (S) związek ξ = ω/λη otrzymuje się
ηµ
η
η
ω
2
2
−
−
=
13
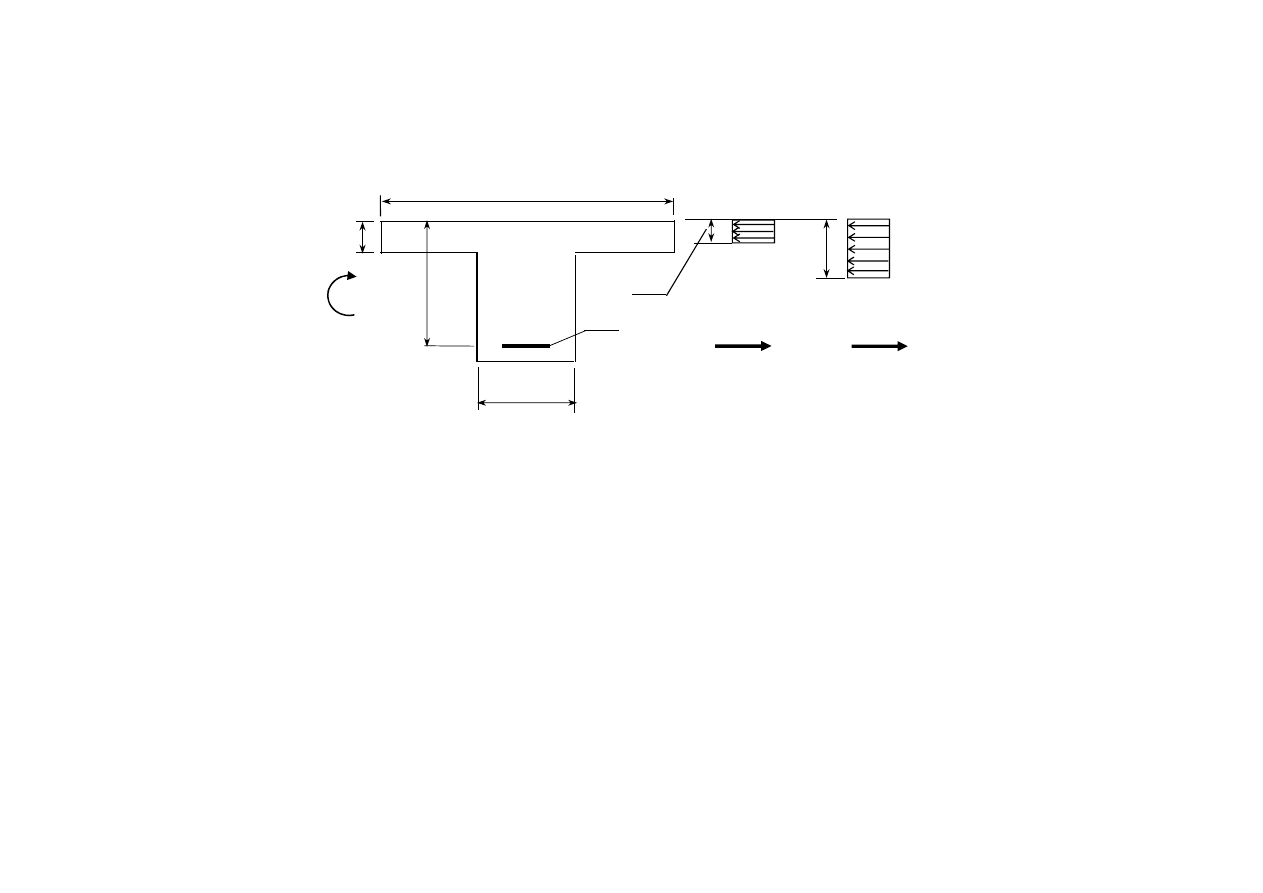
Przy obliczaniu przekrojów teowych istnieją dwie możliwości.
ηf
cd
ηf
cd
M
Rd
b)
h
f
λx
A
s1
b
w
d
A
s1
f
yd
a)
A
s1
f
yd
λx
b
f
Przekrój pozornie teowy i przekrój rzeczywiście teowy
Jeżeli zasięg strefy ściskanej λx jest mniejszy od grubości półki h
f
(rys. a)
poniżej), to występuje przypadek przekroju pozornie teowego. Przekrój taki
oblicza się jak przekrój prostokątny o szerokości b
f
, gdyż obliczenia zależą od
wymiarów strefy ściskanej i od zbrojenia, a kształt strefy rozciąganej nie ma
wpływu na nośność przekroju. W tym przypadku można więc zastosować
wzory dla przekroju prostokątnego z b = b
f
.
Jeżeli λx > h
f
, to strefa ściskana obejmuje półkę i część środnika poniżej półki
– przekrój jest rzeczywiście teowy.
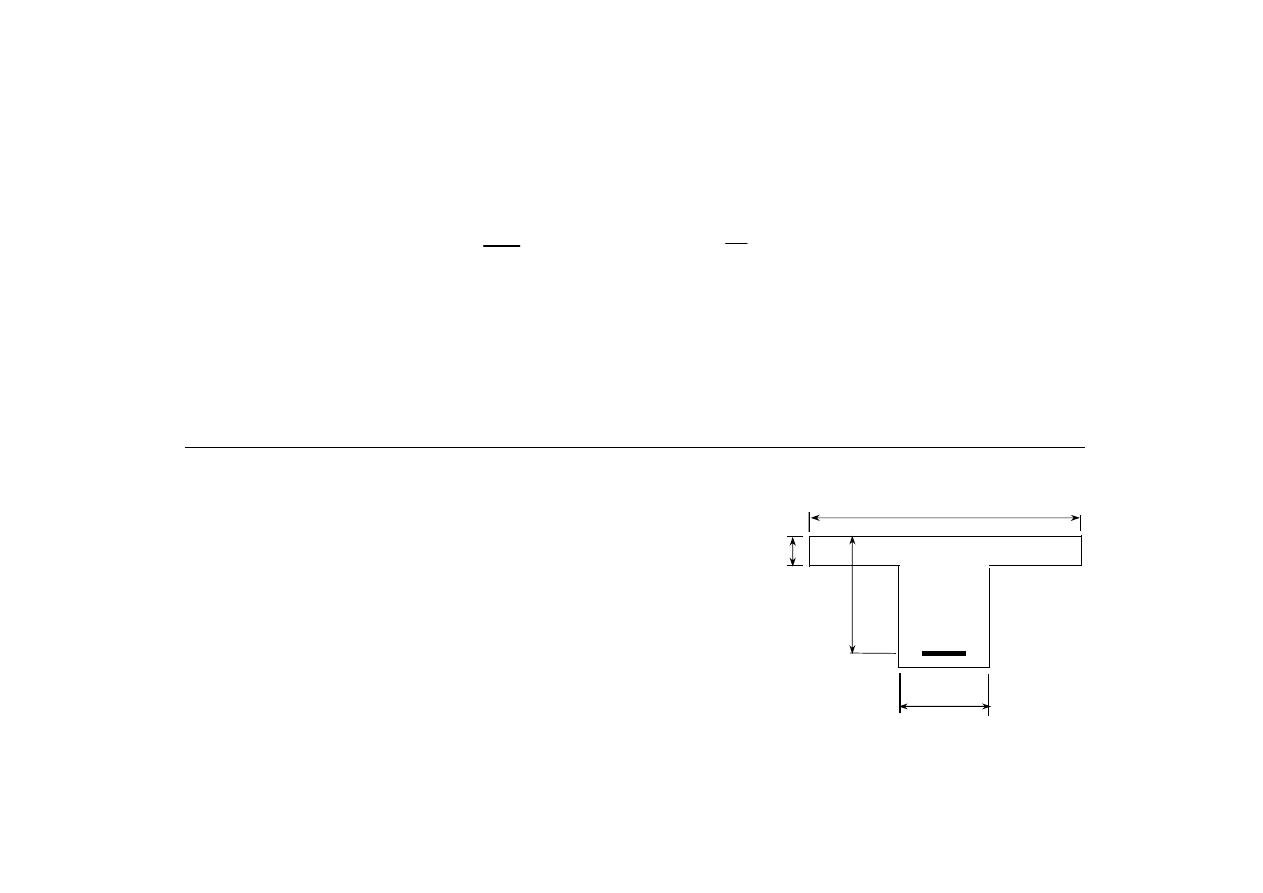
14
Pierwszym krokiem obliczeń jest sprawdzenie hipotezy λx ≤ h
f
. Dla wartości ω
obliczonej według tab. 5 przy b = b
f
wyznacza się
λη
ω
ξ
=
d
x
η
ω
λ
=
Jeżeli tak obliczony zasięg strefy ściskanej λx jest mniejszy niż grubość półki h
f
,
to przekrój jest pozornie teowy. W przeciwnym przypadku oś zerowych naprężeń
leży poniżej półki i przekrój rozpatruje się jako rzeczywiście teowy.
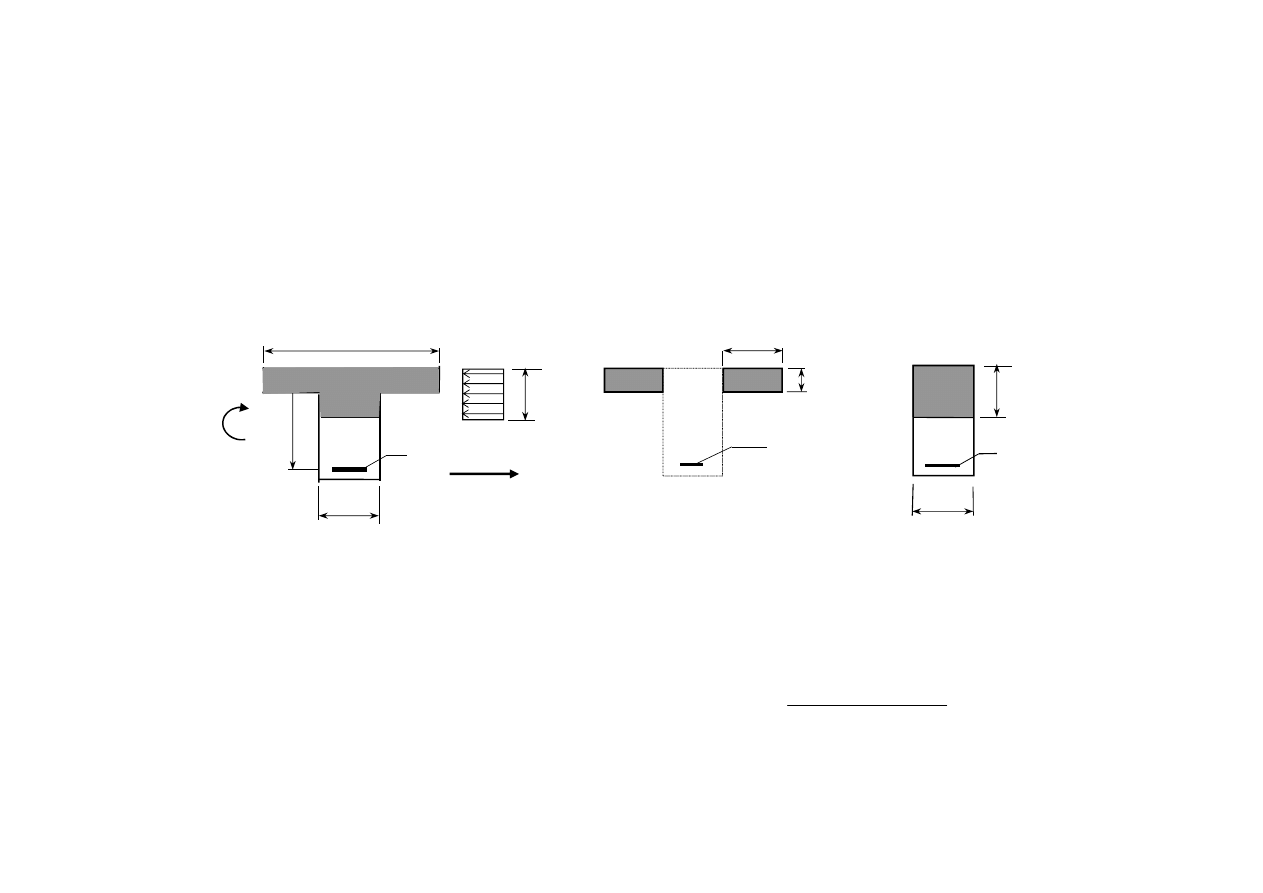
Uwaga. Inny sposób sprawdzenia, czy przekrój
jest pozornie teowy polega na porównaniu
momentu M
f
, który jest potrzebny do wytworzenia
strefy ściskanej o zasięgu równym h
f
z momentem
M
Ed.
. Jeżeli
(
)
,
5
,
0
f
cd
f
f
f
Ed
h
d
f
b
h
M
M
−
=
≤
η
to przekrój jest pozornie teowy.
h
f
b
w
d
b
f
15
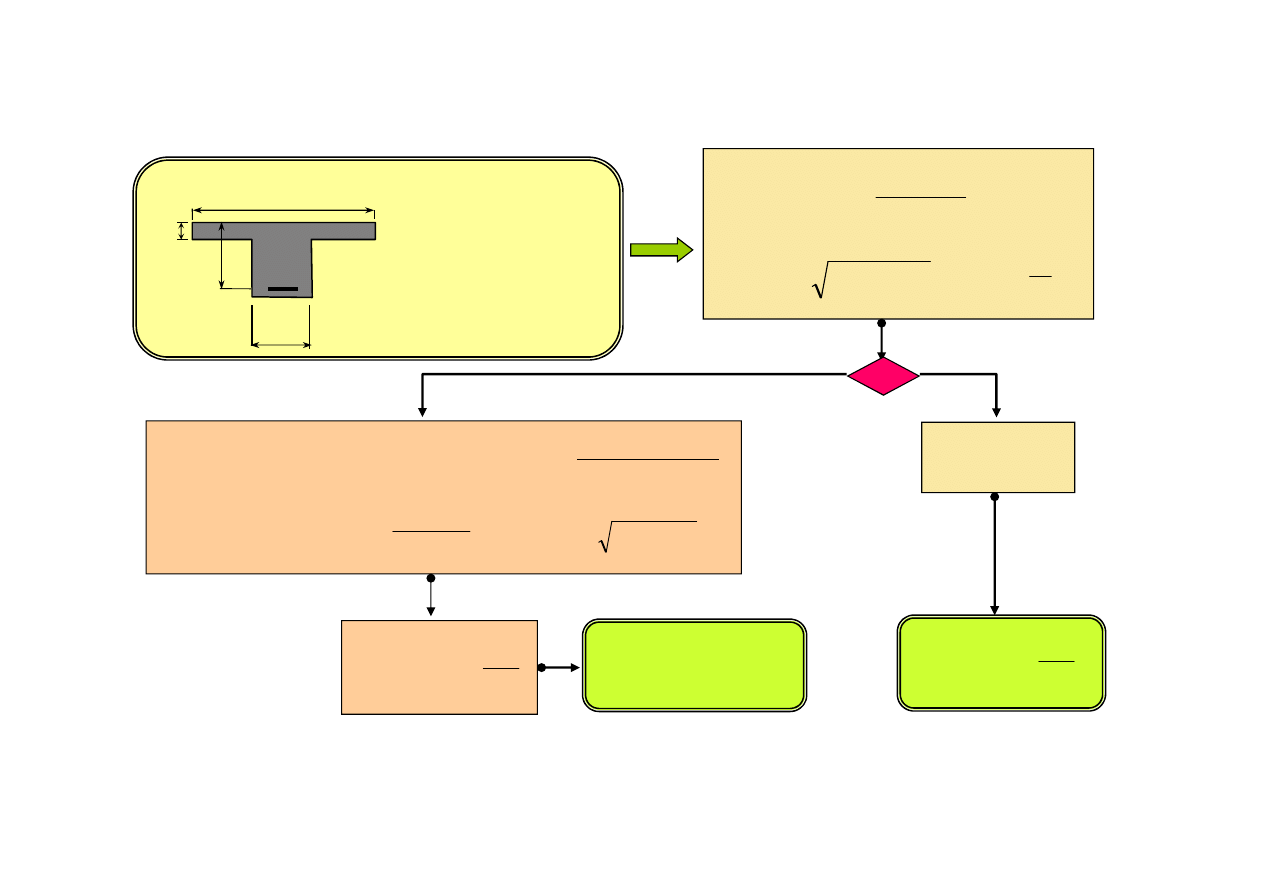
Prosty sposób obliczania przekrojów rzeczywiście teowych opiera się na
podzieleniu strefy ściskanej na dwie części:
część 1 – obszar półki o wymiarach (b
f
– b
w
) i h
f
część 2 - obszar środnika o wymiarach b
w
i λx.
ηf
cd
b
f
A
s1
f
yd
A
s1
b
w
d
λx
b
w
Część 2
0,5(b
f
-b
w
)
h
f
A
s1,1
Część 1
=
+
λx
A
s1,2
Moment zginający przenoszony przez część 1 przekroju i zbrojenie potrzebne
ze względu na ten moment:
(
)(
)
cd
f
w
f
f
f
h
d
b
b
h
M
η
5
,
0
1
−
−
=
(
)
yd
f
s
f
h
d
M
A
5
,
0
1
1
,
1
−
=
16
Na część 2 przypada moment
cd
w
f
d
b
M
2
2
=
µ
a następnie według tab. 4 wartość ω i
yd
cd
w
s
f
f
d
b
A
ω
=
2
,
1
Całe potrzebne zbrojenie jest sumą zbrojeń części 1 i 2
.
2
,
1
1
,
1
1
s
s
s
A
A
A
+
=
b
w
Część 2
λx
A
s1,2
1
2
M
M
M
Ed
−
=
Zbrojenie potrzebne ze względu na ten moment oblicza
się jak dla przekroju prostokątnego o szerokości b
w
.
..
Oblicza się
17
Tab. 5. Obliczanie zbrojenia przekrojów teowych
ω
α
=
:
1
yd
cd
f
s
f
f
d
b
A
1
1
α
=
Dane: b
w
, b
f
, h
f
, d
f
cd
, f
yd
, M
Ed
Oblicza się: A
s1
h
f
cd
f
Ed
f
d
b
M
2
=
µ
µ
η
η
η
ω
2
:
2
−
−
=
d
x
η
ω
λ
=
f
h
x >
λ
f
h
x ≤
λ
(
)(
)
cd
f
w
f
f
f
h
d
b
b
h
M
η
5
,
0
1
−
−
=
(
)
yd
f
,
s
f
h
,
d
M
A
5
0
1
1
1
−
=
1
2
M
M
M
Ed
−
=
cd
w
f
d
b
M
2
2
=
µ
µ
η
η
η
ω
2
:
2
−
−
=
yd
cd
w
s
f
f
d
b
A
ω
=
2
,
1
2
,
1
1
,
1
1
s
s
s
A
A
A
+
=
Uwaga: Założono, że zawsze µ ≤ µ
lim
.
b
w
b
f
d
18
Drugie podstawowe zadanie to obliczanie nośności M
Rd
dla danego zbrojenia
A
s1
. Podobnie jak poprzednio, najpierw zakłada się, że przekrój jest pozornie
teowy i z warunku równowagi
yd
s
cd
f
f
A
f
b
x
1
=
η
λ
wyznacza się λx. Jeżeli λx ≤ h
f
, to przekrój jest pozornie teowy, a w przeciwnym
przypadku, do obliczenia momentu granicznego stosuje się sposób oparty na
podziale strefy ściskanej na części 1 i 2.
Zbrojenie potrzebne ze względu na nośność części 1 można wyznaczyć z warunku
równowagi
(
)
cd
w
f
f
yd
s
f
b
b
h
f
A
η
−
=
1
,
1
Nośność części 2 oblicza się przyjmując A
s1,2
= A
s1
- A
s1,1
.
Nośność przekroju jest sumą nośności części 1 i 2.
19
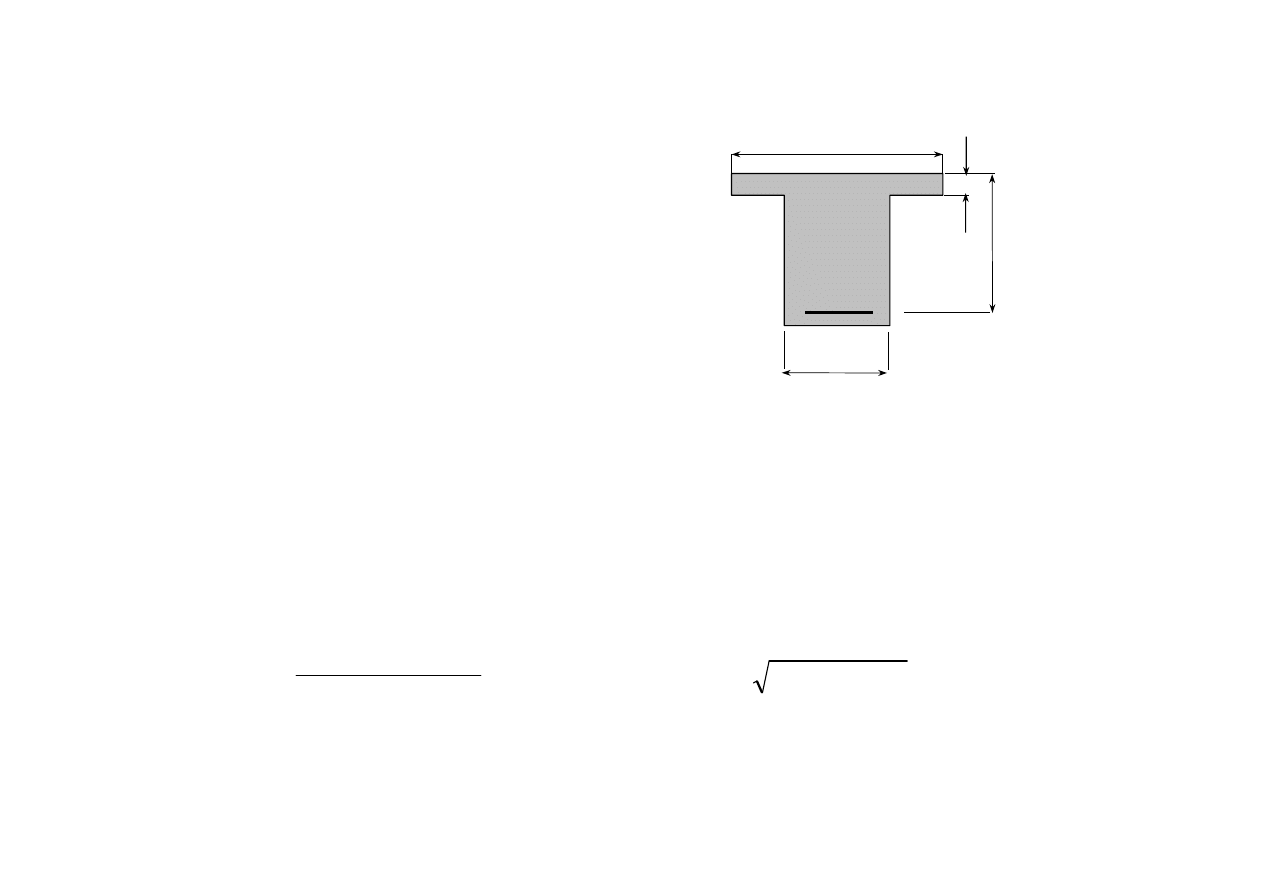
Przykład
Przekrój teowy
Dane są wymiary [w mm] przekroju,
beton: f
cd
= 20 MPa,
stal: f
yd
= 420 MPa,
moment obliczeniowy M
Ed
= 1700 kNm.
Należy obliczyć A
s1
.
400
800
700
150
Tu warto zauważyć, że przekroje belek stropowych są na ogół pozornie teowe
– tu dobrano dane w taki sposób, żeby otrzymać przekrój rzeczywiście teowy.
W takich przekrojach zbrojenie będzie na ogół bardzo duże.
Dla f
ck
≤ 50 MPa
η = 1,0 λ = 0,8
2168
,
0
0
,
20
70
,
0
80
,
0
70
,
1
2
=
⋅
⋅
=
µ
2475
,
0
2168
,
0
2
1
1
=
⋅
−
−
=
ω
Do przekroju teowego stosuje się algorytm według tab. 5.
m
15
,
0
1732
,
0
70
,
0
2475
,
0
=
>
=
⋅
=
f
h
x
λ
, a więc przekrój jest rzeczywiście teowy
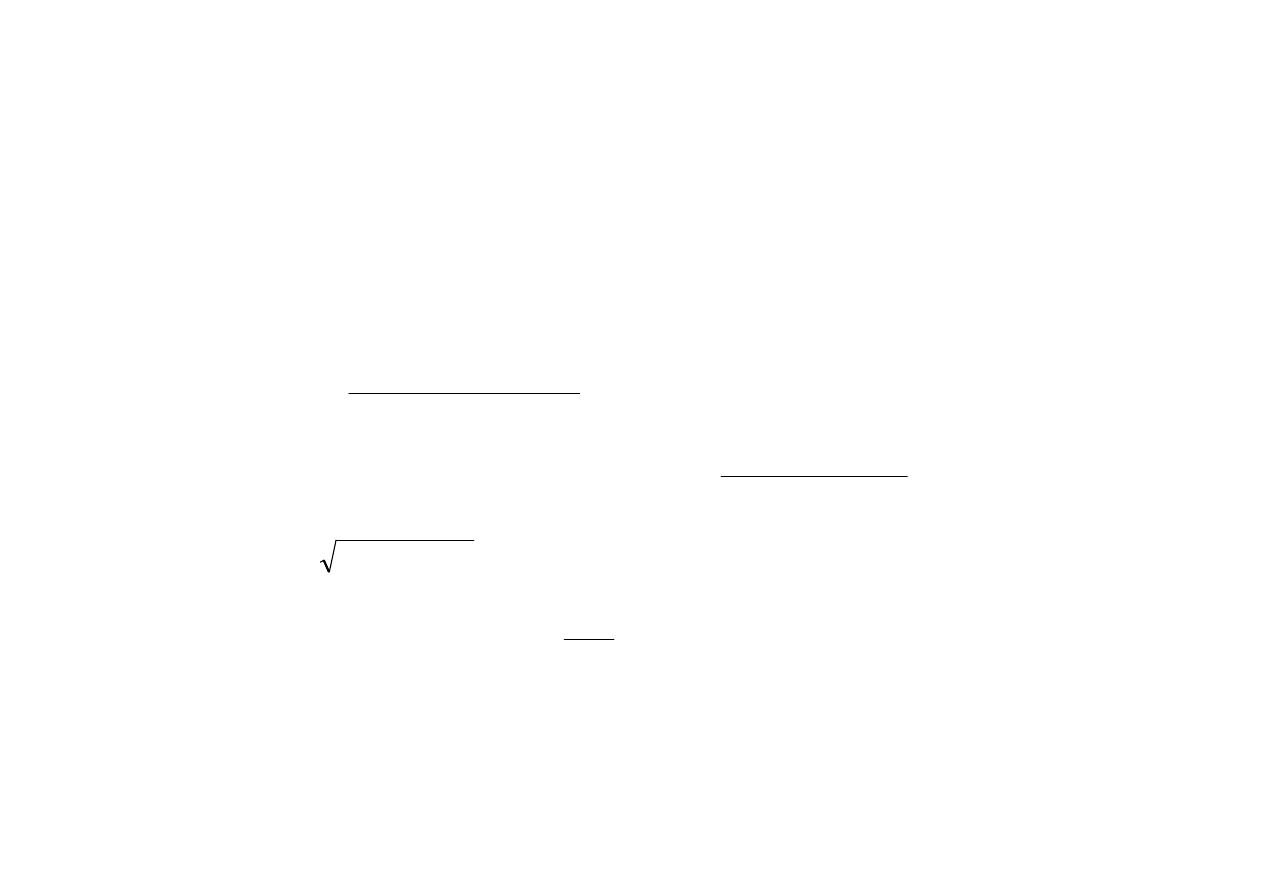
20
Drugi sposób sprawdzenia, czy przekrój jest rzeczywiście teowy
(
)
MNm
70
,
1
MNm
50
,
1
15
,
0
5
,
0
70
,
0
20
80
,
0
15
,
0
=
<
=
⋅
−
⋅
⋅
=
Ed
f
M
M
a więc przekrój jest rzeczywiście teowy.
(
)(
)
MNm
750
,
0
0
,
20
15
,
0
5
,
0
70
,
0
40
,
0
80
,
0
15
,
0
1
=
⋅
⋅
−
−
=
M
(
)
2
4
1
,
1
cm
57
,
28
10
420
15
,
0
5
,
0
70
,
0
750
,
0
=
⋅
⋅
⋅
−
=
s
A
kNm
950
750
1700
2
=
−
=
M
2423
,
0
0
,
20
70
,
0
40
,
0
950
,
0
2
=
⋅
⋅
=
µ
2822
,
0
2423
,
0
2
1
1
=
⋅
−
−
=
ω
.
2
4
2
,
1
cm
63
,
37
10
420
0
,
20
70
,
0
40
,
0
2822
,
0
=
⋅
⋅
⋅
=
s
A
2
2
,
1
1
,
1
1
cm
20
,
66
63
,
37
57
,
28
=
+
=
+
=
s
s
s
A
A
A
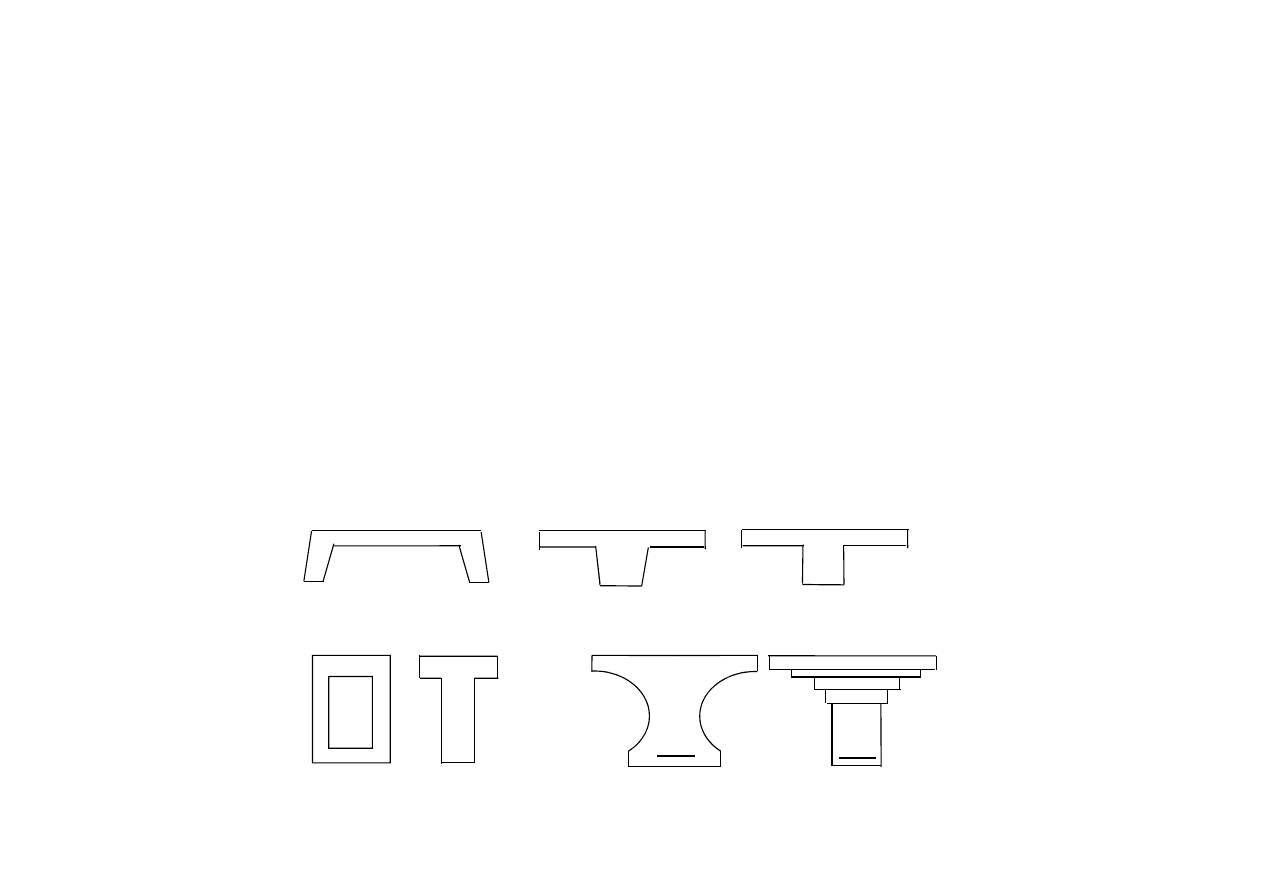
21
7.2.4. Przekroje skrzynkowe i inne obliczane jako teowe
Jeżeli kontur przekroju poprzecznego składa się z linii zakrzywionych lub prostych
nierównoległych do osi pionowej, to w zasadzie do obliczania nośności trzeba
stosować całkowanie.
Kształt rozciąganej części przekroju nie ma wpływu na obliczenia. Dlatego wiele
często stosowanych kształtów (np. płyty prefabrykowane, elementy skrzynkowe)
można z dobrym przybliżeniem analizować jako przekroje teowe. W celu obliczenia
nośności lub zbrojenia przekrój skrzynkowy można zastąpić przekrojem teowym, w
którym środnik ma grubość równą sumie grubości ścianek skrzynki. Również
złożone kształty można obliczać na podstawie teorii przekrojów teowych, stosując ją
„krok po kroku” do kolejnych części (niezbędną częścią analizy jest znalezienie
prostokąta, w którym leży oś zerowych naprężeń).
≈
≈
≈
=
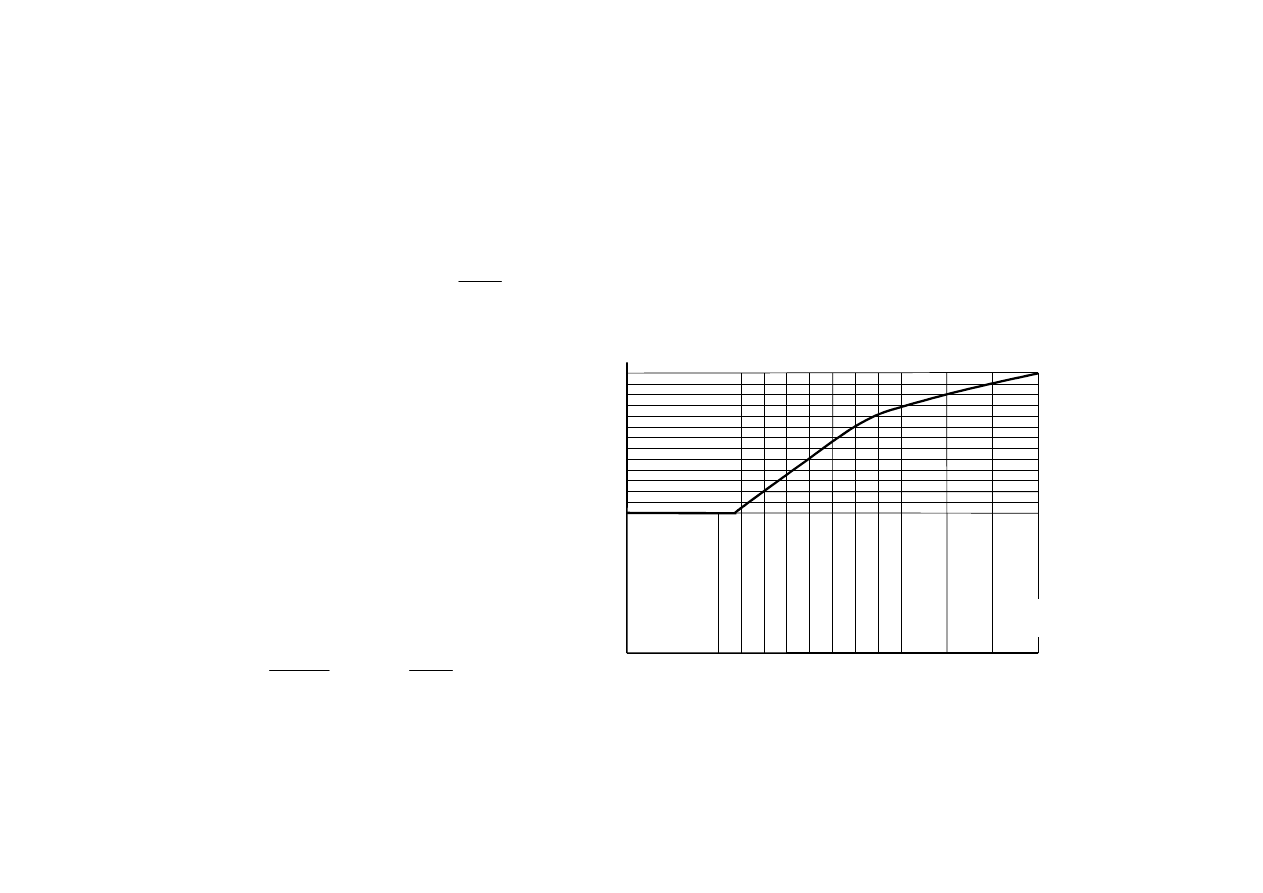
22
7.3. Minimalne i maksymalne zbrojenie podłużne elementów zginanych
7.3.1. Zbrojenie minimalne
Pole przekroju zbrojenia rozciąganego powinno być co najmniej równe A
s,min
.
b
t
oznacza średnią szerokość strefy
rozciąganej,
f
ctm
oznacza wytrzymałość betonu na
rozciąganie.
,
26
,
0
min
,
d
b
f
f
A
t
yk
ctm
s
=
lecz nie mniej niż 0,0013 b
t
d.
Minimalny stopień zbrojenia
rozciąganego wynosi zatem
yk
ctm
t
s
f
f
d
b
A
26
,
0
min
,
min
,
1
=
=
ρ
0,17
0,15
0,19
0,21
0,13
0,23
A
s,min
/(b
t
d) [%]
0,25
20 25
35
45
55
70
80
90
60
f
ck
[MPa]
ρ
1,min
(f
yk
= 500 MPa) w zależności od f
ck
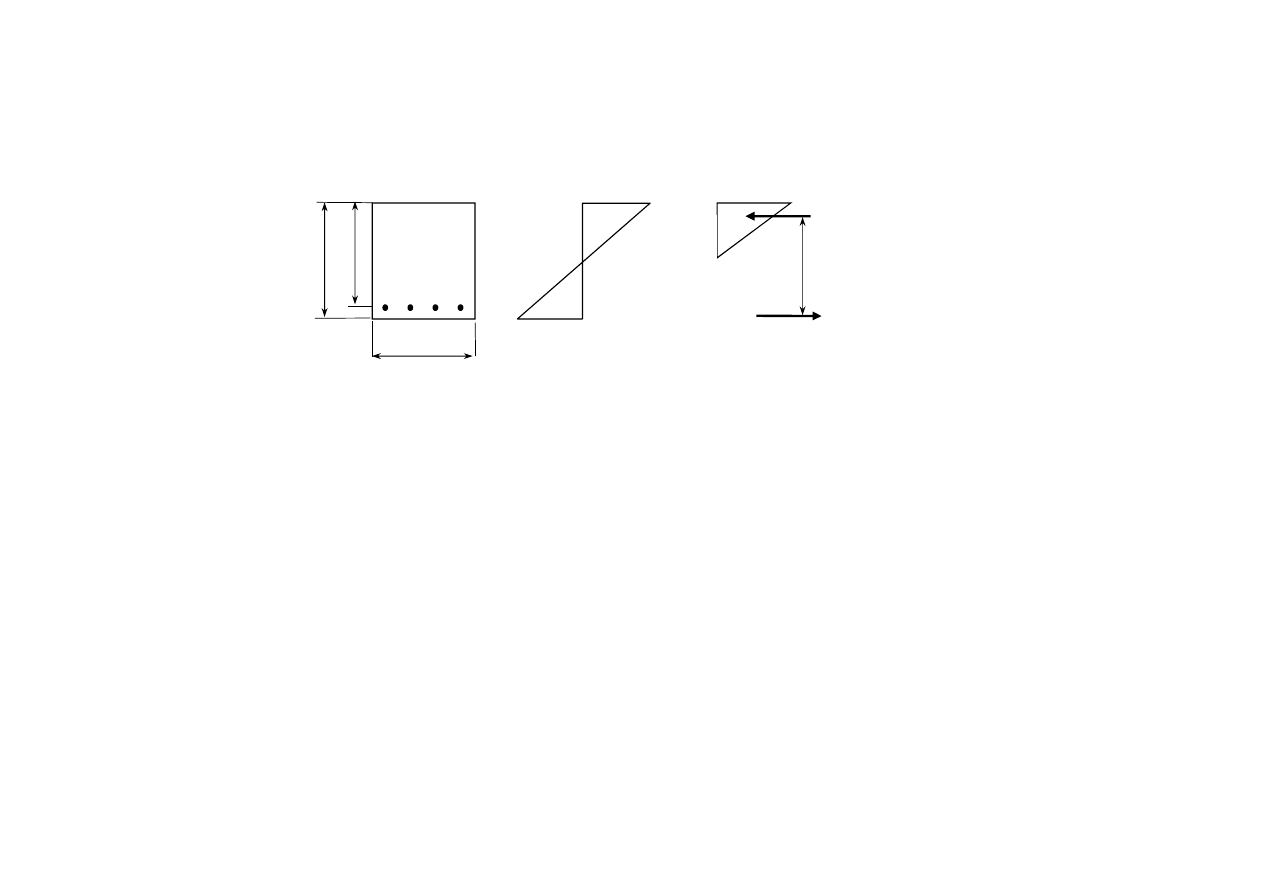
23
Uzasadnienie tego przepisu wynika z zależności przedstawionych na rysunku poniżej.
f
ctm
A
s1
σ
s1
d
z ≈ 0,8d
b
a)
b)
P
c
Siły wewnętrzne: a) bezpośrednio przed zarysowaniem, b) bezpośrednio po zarysowaniu
h
Moment rysujący wynosi
Zakłada się, że bezpośrednio przed pojawieniem się rysy naprężenie rozciągające w
skrajnych włóknach przekroju jest równe f
ctm
.
Po zarysowaniu naprężenia rozciągające beton spadają w rysie do zera i cała siła
rozciągająca zostaje przejęta przez zbrojenie. Moment zginający jest równy
momentowi pary sił A
s1
σ
s1
i P
c
i nadal jest równy M
cr
.
W
f
M
ctm
cr
=
W oznacza tu odpowiedni wskaźnik wytrzymałości przekroju, wyznaczony bez
uwzględniania wpływu zbrojenia – np. dla prostokąta W = 0,1667bh
2.
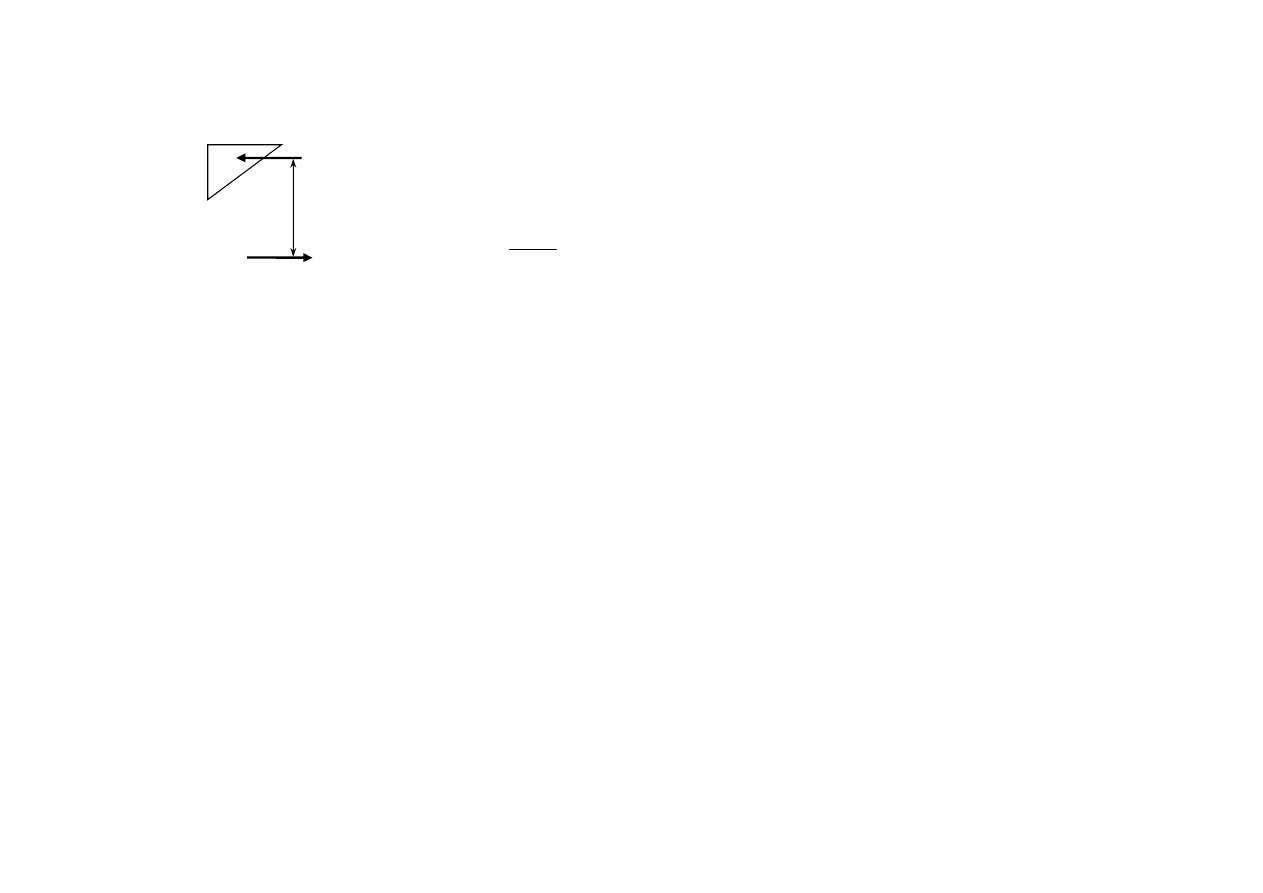
24
Oczywiście, naprężenie w zbrojeniu nie może być większe od granicy plastyczności
(jeśli nie uwzględnia się wzmocnienia). Tak więc, w tym przypadku graniczny
moment przekroju zbrojonego (obliczony dla σ
s1
= f
yk
) staje się mniejszy od
momentu granicznego przekroju niezbrojonego. Gdyby taki element wykonać i
zbadać, to natychmiast po przekroczeniu M
cr
, czemu towarzyszą tylko niewielkie
odkształcenia i ugięcia, nastąpi nagłe zniszczenie, gdyż zbrojenie nie jest w stanie
przejąć siły, która pojawi się w nim po zarysowaniu.
Nagłe zniszczenie przy małych odkształceniach, bez wyraźnych odkształceń
plastycznych, bywa nazywane zniszczeniem „kruchym”. Kruche zniszczenie uważa
się za zjawisko niepożądane i niebezpieczne, gdyż utrata nośności nie jest
poprzedzona fazą, w której rysy, rozszerzając się w miarę zwiększania obciążenia,
sygnalizują, że nośność elementu może być zagrożona.
A
s1
σ
s1
z ≈ 0,8d
P
c
z
A
M
s
s
cr
1
1
σ
=
z
A
M
s
cr
s
1
1
=
σ
Jeżeli ilość zbrojenia rozciąganego jest
bardzo mała, to naprężenie σ
s1
, obliczone
na podstawie zależności odpowiedniej dla
przekroju zarysowanego może być
większe od f
yk
.
25
Stosowanie zbrojenia o polu równym co najmniej określonemu w normie
minimum zapobiega kruchemu zniszczeniu. Minimum to można wyznaczyć na
podstawie wymagania, że naprężenie w zbrojeniu, wywołane przez moment
rysujący, nie powinno być większe niż f
yk
.
W przekroju prostokątnym:
bezpośrednio przed zarysowaniem, czyli w fazie I:
(
)
ctm
ctm
cr
f
b
d
f
h
b
M
6
1
,
1
6
1
2
2
≅
=
bezpośrednio po zarysowaniu, czyli w fazie II:
d
f
A
M
yk
s
cr
8
,
0
min
,
⋅
=
Porównując te dwie zależności otrzymuje się wzór zawarty w normie
yk
ctm
yk
ctm
yk
ctm
s
f
f
d
b
f
f
d
b
f
d
f
d
b
A
26
,
0
252
,
0
8
,
0
6
21
,
1
2
min
,
≅
=
⋅
=
26
Na podobnej zasadzie, tzn. porównując moment rysujący obliczony na podstawie
teorii fazy I z obliczonym na podstawie teorii fazy II, można uzyskać „ścisłe”
wzory na minimum zbrojenia dla przekrojów nieprostokątnych. Według normy
można poprzestać na prostym przybliżeniu określonym przez omówiony powyżej
wzór dla prostokąta.
Przekroje, które mają zbrojenie mniejsze od A
s,min
należy rozpatrywać jako
przekroje niezbrojone – współczynnik bezpieczeństwa stosowany do betonu jest
wtedy większy niż współczynnik stosowany, gdy element jest żelbetowy.
Dla dużych elementów (np. grubych płyt) ilość zbrojenia wynikająca z przepisów
dotyczących minimum może być bardzo znaczna.
Minimum zbrojenia nie zależy od momentu zginającego, a więc może się zdarzyć,
że przy niewielkich momentach potrzebna jest duża objętość zbrojenia, przede
wszystkim dlatego, że duża jest objętość betonu.
W takich przypadkach norma zezwala na pewne osłabienie wymagań. Według
Eurokodu: „Alternatywnie, w elementach drugorzędnych, w których można
akceptować pewne ryzyko kruchego zniszczenia, można stosować A
s,min
równe 120%
pola zbrojenia, które wynika ze sprawdzania stanu granicznego użytkowalnosci”.
27
Omawiane w tym punkcie minimalne zbrojenie ma zapobiegać kruchemu
zniszczeniu i ma być stosowane wszędzie tam, gdzie może wystąpić
rozciąganie, wywołane przez obciążenia.
Inne przepisy dotyczące minimalnego zbrojenia, związane z potrzebą
ograniczenia szerokości ewentualnych rys, które mogą być wywołane przez
obciążenia w SGU, a przede wszystkim przez skurcz betonu i odpływ ciepła
hydratacji cementu, zostaną omówione później. Do tych właśnie przepisów
nawiązuje cytowany powyżej punkt Eurokodu.
Ze wzoru na minimum zbrojenia wynika, że im mocniejszy jest beton, tym
większe jest potrzebne minimalne zbrojenie. Jest to ważna cecha
charakterystyczna konstrukcji żelbetowych (wystąpi ona także przy
sprawdzaniu SG użytkowalności). Stosowanie bardzo mocnego betonu, jeżeli
nie jest konieczne ze względu na wymagania dotyczące wytrzymałości i
trwałości, jest nieekonomiczne, gdyż pociąga za sobą potrzebę stosowania
wysokiego minimum zbrojenia w strefach słabo obciążonych
28
7.3.2. Zbrojenie maksymalne
Według Eurokodu pole przekroju zbrojenia rozciąganego (lub ściskanego) nie
powinno przekraczać A
s,max
= 0,04A
c
. Ograniczenie to dotyczy obszarów, w których
nie występują połączenia na zakład, co oznacza, że na odcinkach zakładów limit ten
może być przekroczony.
Zalecenie to wynika z wymagań dotyczących rozmieszczania zbrojenia – rozstaw
prętów powinien umożliwiać właściwe ułożenie i zagęszczenie betonu.
Ilości zbrojenia zbliżające się do A
s,max
mogą być racjonalnie wykorzystane tylko w
przekrojach podwójnie zbrojonych i teowych. Zbrojenie przekrojów pojedynczo
zbrojonych należy dobierać na podstawie warunku α
1
≤ α
1,lim
, w którym α
1,lim
oznacza
względną siłę graniczną w zbrojeniu, która powstaje gdy ξ = ξ
lim
(µ = µ
lim
). Graniczne
wartości α
1
, ξ, µ można wyznaczyć stosując tablice, a ewentualne przekroczenie tych
wartości „ujawnia się samo” przy stosowaniu zamieszczonych tam algorytmów.
Przykład. Dla zestawienia beton f
ck
= 25 MPa, stal f
yk
= 500 MPa otrzymuje się
α
1
≈ 0,5 i przyjmując f
yd
= 435 MPa, f
cd
= 30/1,4 = 21,4 MPa mamy
%
46
,
2
435
4
,
21
5
,
0
5
,
0
lim
,
1
lim
,
1
=
=
=
=
yd
cd
s
f
f
d
b
A
ρ
Niekiedy, chcąc uniknąć podwójnego zbrojenia, można zastosować zbrojenie pojedyncze
przy µ > µ
lim
, ale znaczne przekroczenie µ
lim
prowadzi do zupełnie nieracjonalnych ilości
zbrojenia.