1
Wyk
Wyk
ł
ł
ad IX
ad IX
Funkcja jednej zmiennej
Funkcja jednej zmiennej
Przypomnienie wiadomości
1
x
2
x
3
x
4
x
5
x
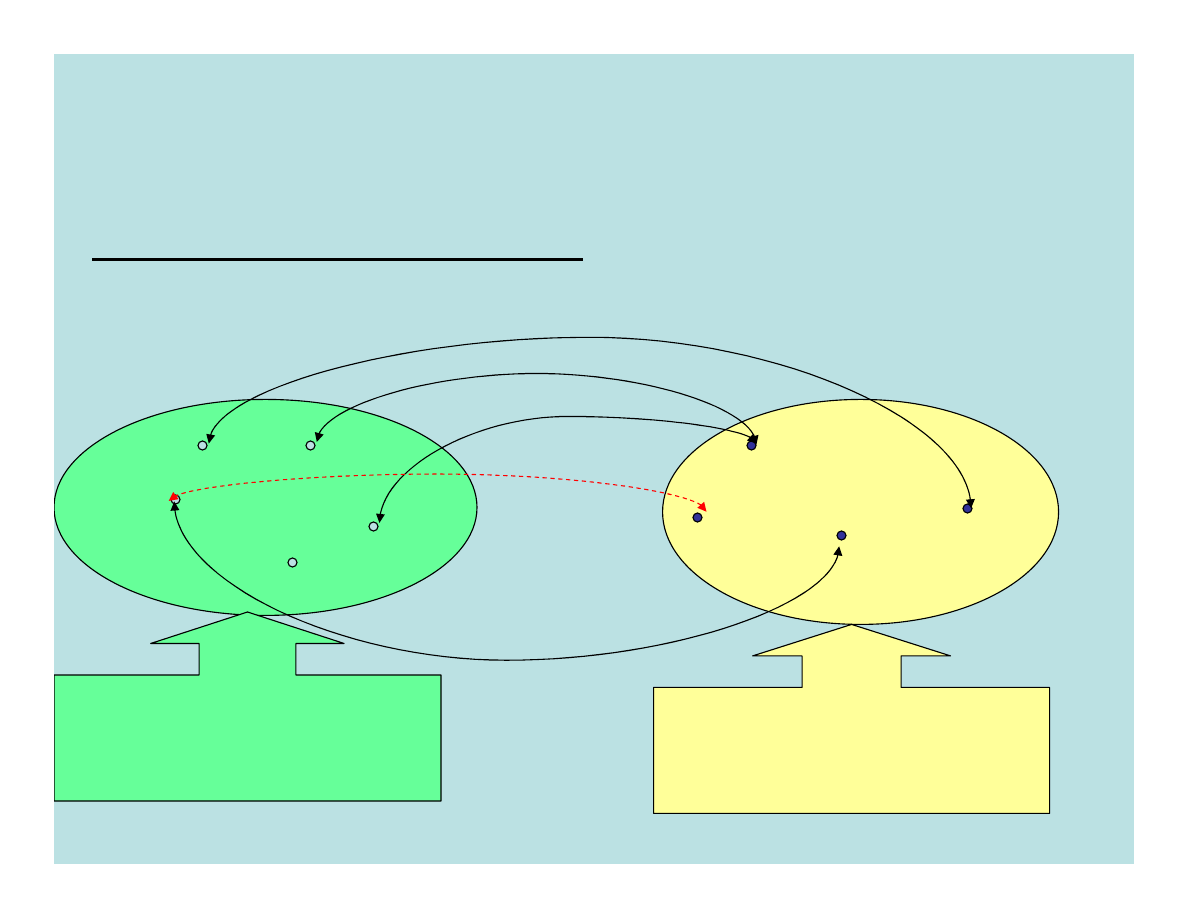
Funkcja jednej zmiennej y = f(x)
3
y
1
y
4
y
2
y
Dziedzina funkcji - Df:
zbiór argumentów x
Przeciwdziedzina:
zbiór wartości funkcji y
2
Granica i ciągłość funkcji
Funkcja f(x) ma granicę g w punkcie x
0
, jeśli dla
dowolnego ciągu x
n
dążącego do x
0
, wartości funkcji
f
(x
n
) dążą do g.
Funkcja f(x) jest ciągła w punkcie x
0
, jeśli punkt x
0
należy do dziedziny funkcji oraz granica lewostronna w
punkcie x
0
jest równa granicy prawostronnej w tym
punkcie i jest równa f(x
0
).
Jeśli funkcja f(x) posiada przynajmniej jeden punkt
nieciągłości to funkcja nie jest ciągła.
3
Funkcję f(x) nazywamy różnowartościową jeśli każdemu y
z przeciwdziedziny odpowiada dokładnie jeden x∈Df .
Funkcję taką nazywamy wzajemnie jednoznaczną.
Każda funkcja różnowartościowa f(x) posiada funkcję do
niej odwrotną y= f
-1
(x). Wykresy funkcji f(x) i do niej
odwrotnej y=f
-1
(x) są symetryczne względem prostej
y=x
.
Przykład.
Znaleźć funkcję odwrotną do funkcji
y
=3x-4
Rozwiązanie:
Aby znaleźć funkcję odwrotną do funkcji
y
=3x-4,
wstawiamy w miejsce
x
zmienną
y
oraz zamiast
y
wstawiamy
x
.
Następnie z równania wyznaczamy
y
.
x
=3y-4 |:3
3
4
3
−
= y
x
3
4
3
+
=
⇔
x
y
4
Podstawowe funkcje
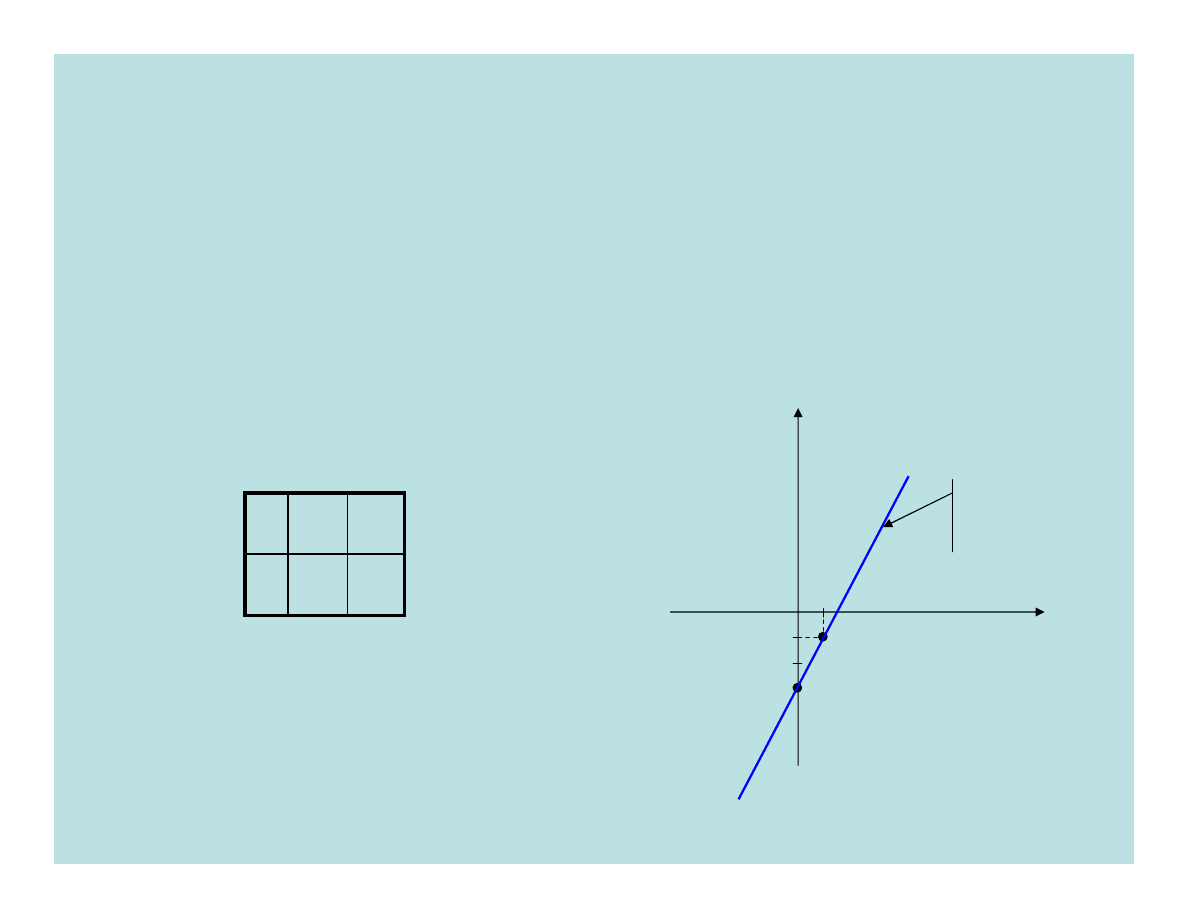
1. Funkcja liniowa
Funkcją liniową nazywamy funkcję postaci: y=ax+b .
Dziedziną funkcji jest zbór liczb rzeczywistych. Jest to
funkcja ciągła. Wykresem jest linia prosta.
Przykład:
y=
2x-3
-1
-3
y
1
0
x
y
=2x-3
5
2. Funkcja kwadratowa
Funkcją kwadratową nazywamy funkcję postaci:
y=ax
2
+bx+c
,
gdzie a≠0. Dziedziną funkcji jest zbór liczb rzeczywistych.
Jest funkcją ciągłą i jej wykresem jest parabola.
a
b
x
2
0
−
=
a
b
x
2
2
∆
+
−
=
Jeśli a>0 wówczas ramiona paraboli skierowane są do góry,
natomiast jeśli a<0 ramiona paraboli skierowane są do dołu.
Ilość miejsc zerowych zależy od wyróżnika ∆=b
2
-4ac.
Jeśli ∆<0 to nie ma miejsc zerowych.
Jeśli ∆=0 istnieje jedno miejsce zerowe:
Jeśli ∆>0 istnieją dwa pierwiastki:
a
b
x
2
1
∆
−
−
=
6
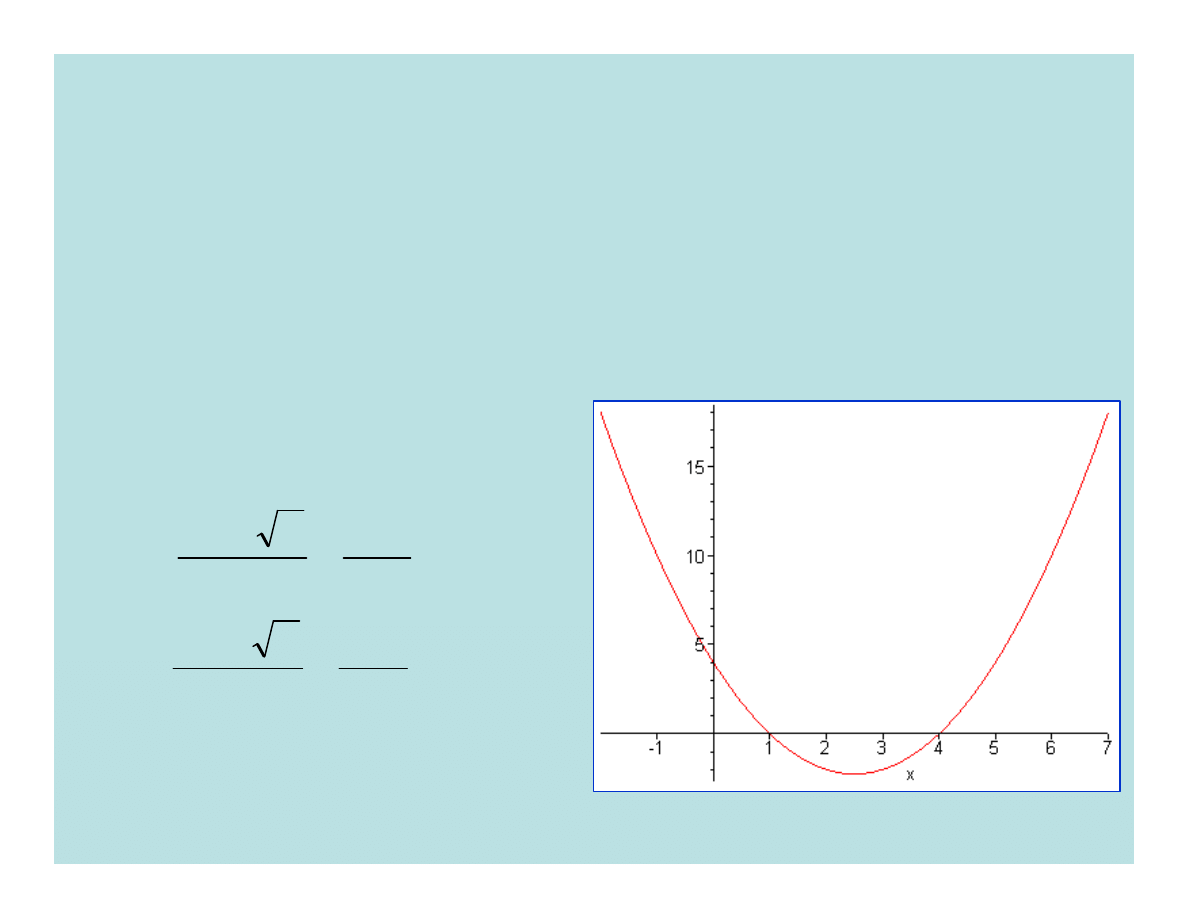
Przykład. Wykonać wykres funkcji:
4
5
2
+
−
=
x
x
y
0
4
5
2
=
+
− x
x
(
)
9
4
1
4
5
4
2
2
=
⋅
⋅
−
−
=
−
=
∆
ac
b
Znajdziemy punkty przecięcia paraboli z osią OX
(miejsca zerowe)
1
2
3
5
2
1
=
−
=
∆
−
−
=
a
b
x
4
2
3
5
2
2
=
+
=
∆
+
−
=
a
b
x
7
3. Funkcja wielomianowa
Funkcją wielomianową stopnia n nazywamy funkcję postaci:
y=a
0
x
n
+a
1
x
n
-1
+…+a
n
-1
x
+a
n
.
Dziedziną funkcji jest zbór liczb rzeczywistych.
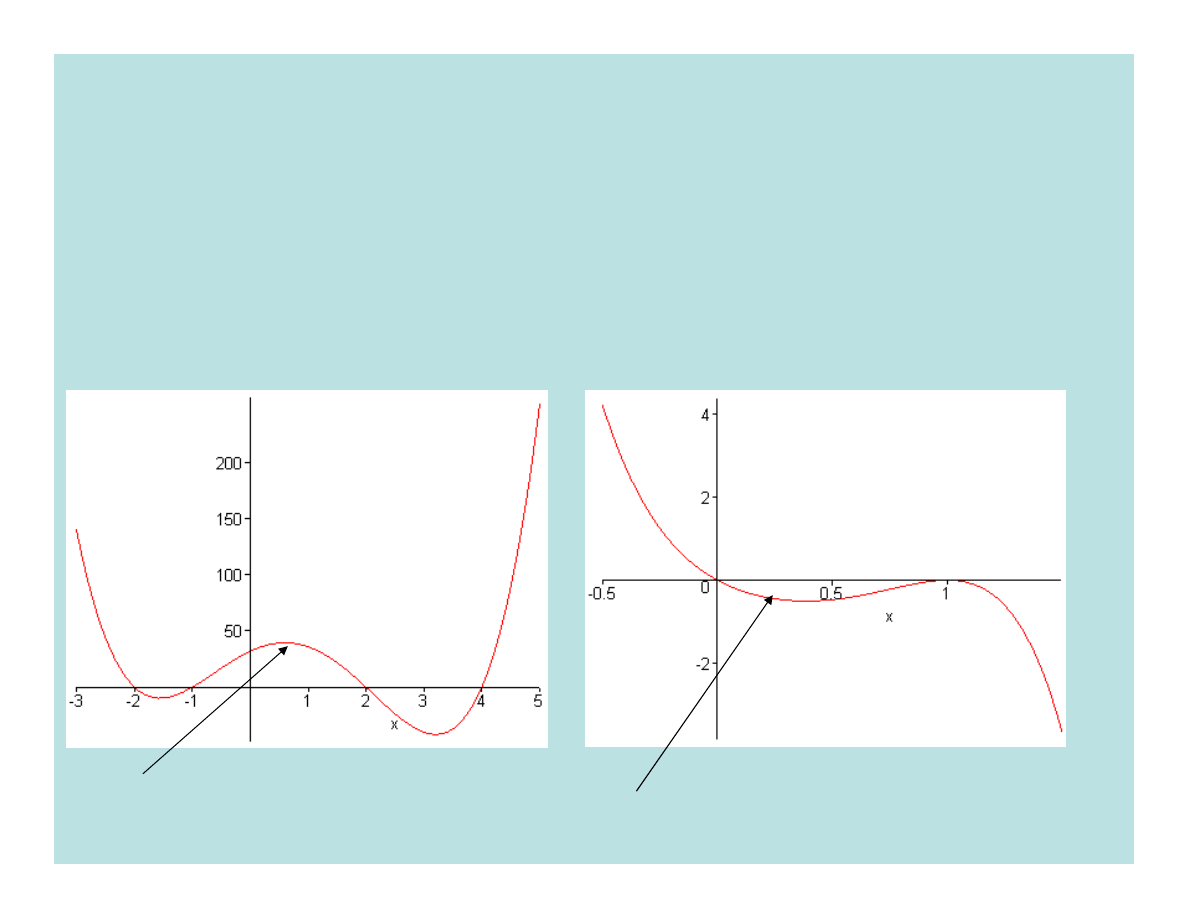
Wielomian jest funkcją ciągłą. Wykresem funkcji są np.
krzywe postaci:
y=
-3x
5
+6x
4
-6x
3
+6x
2
-3x
y=
2x
4
-6x
3
-16x
2
+24x+32
8
4. Funkcja wymierna
Funkcją wymierną nazywamy funkcję, która jest ilorazem
dwóch wielomianów:
Dziedziną funkcji jest zbór liczb rzeczywistych pomniejszony
o miejsca zerowe mianownika. Jeśli istnieją miejsca zerowe
mianownika to funkcja wymierna nie jest ciągła.
m
m
m
m
n
n
n
n
b
x
b
x
b
x
b
a
x
a
x
a
x
a
y
+
+
+
+
+
+
+
+
=
−
−
−
−
1
1
1
0
1
1
1
0
L
L
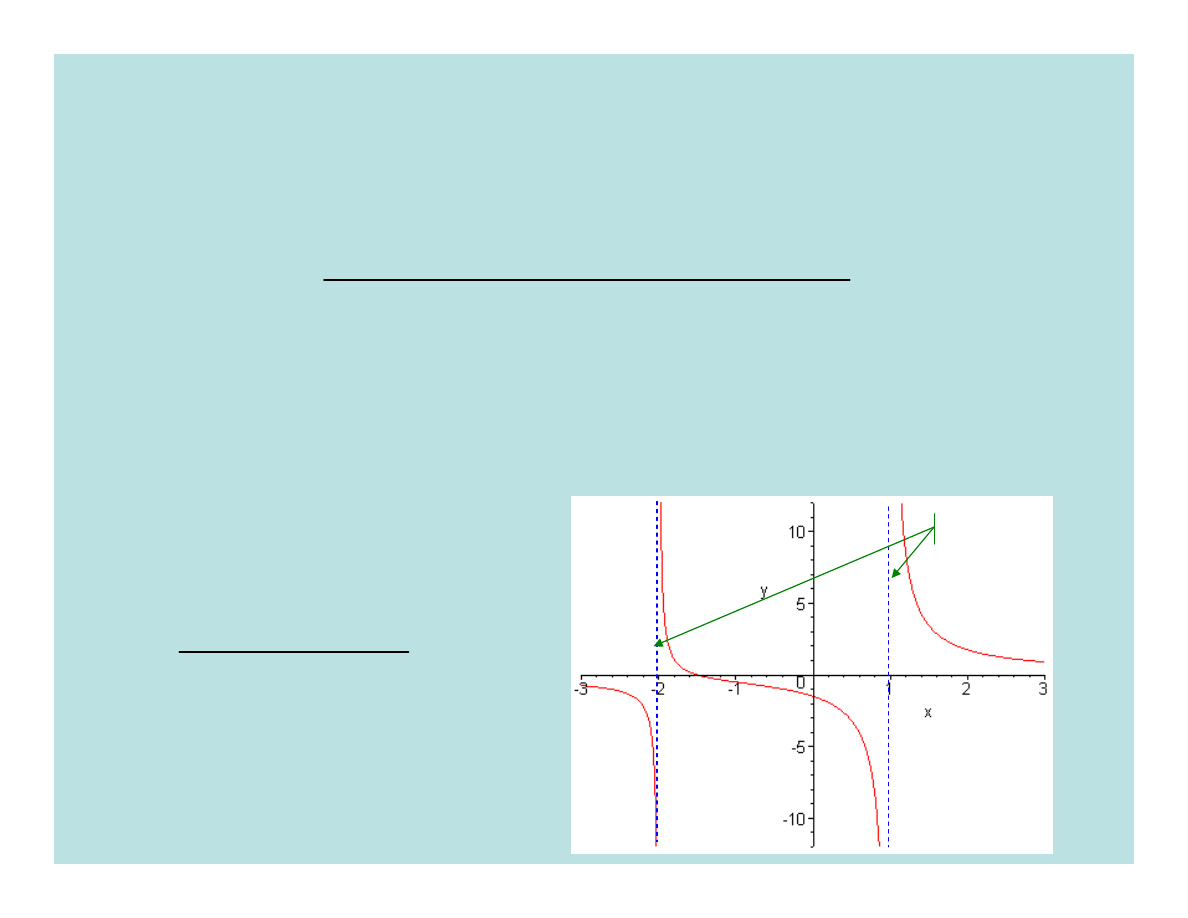
Wykresem funkcji
jest krzywa postaci:
)
2
)(
1
(
3
2
+
−
+
=
x
x
x
y
asymptoty
9
5. Funkcja wyk
ładnicza
.
;
;
;
a
3
2
2
1
3
1
=
Funkcją
wykładniczą
nazywamy funkcję postaci:
y=a
x
, a
>0.
Dziedziną funkcji są liczby rzeczywiste.
Funkcja wykładnicza przyjmuje wartości dodatnie oraz jest
funkcją malejącą dla 0<a<1 oraz rosnącą dla a>1.
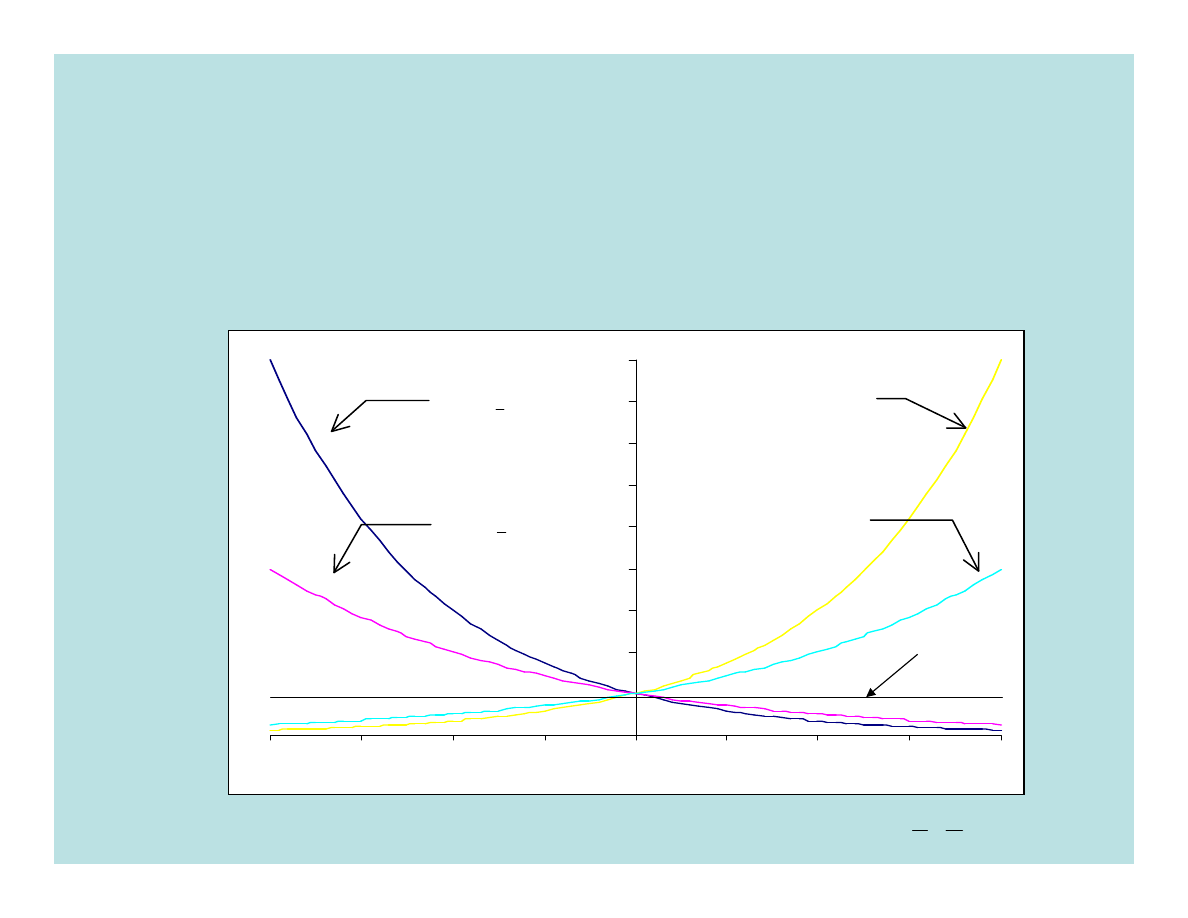
Wykresy funkcji wykładniczych dla wartości
0
1
2
3
4
5
6
7
8
9
-2
-1, 5
-1
-0 ,5
0
0,5
1
1,5
2
( )
x
y
3
1
=
x
y
3
=
x
y
2
=
( )
x
y
2
1
=
x
y
1
=
10
6. Funkcja logarytmiczna
Funkcją logarytmiczną nazywamy funkcję postaci
y=log
a
x
,
gdzie a>0 i a≠1.
Dziedziną tej funkcji są liczby dodatnie, tzn. x∈R
+
.
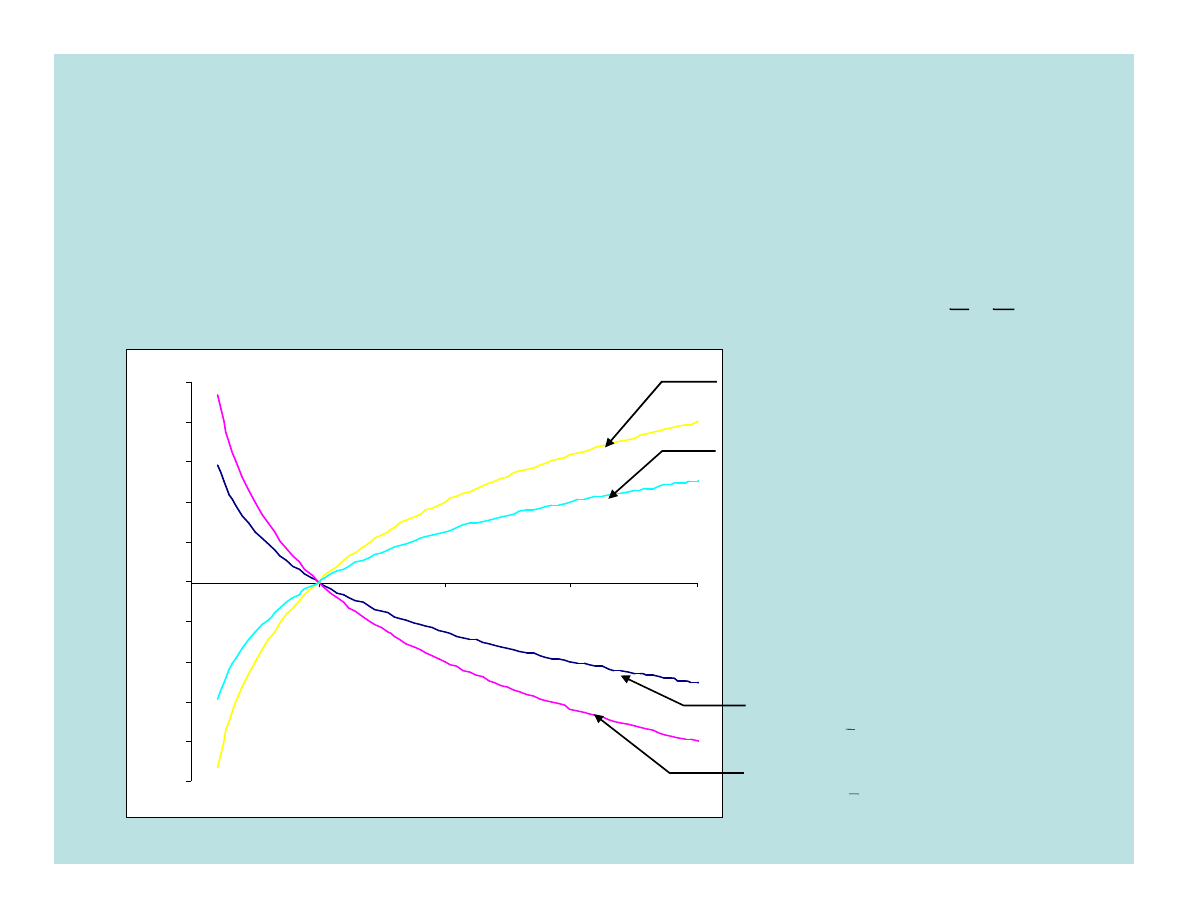
Wykresy funkcji logarytmicznych dla wartości
3
;
2
;
2
1
;
3
1
=
a
-2,5
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
2,5
0
1
2
3
4
x
y
2
log
=
x
y
3
log
=
x
y
3
1
log
=
x
y
2
1
log
=
11
Spośród funkcji wykładniczych i logarytmicznych
wyróżnimy funkcję wykładniczą i logarytmiczną o
podstawie liczby e, czyli funkcje:
y=e
x
oraz
y=lnx
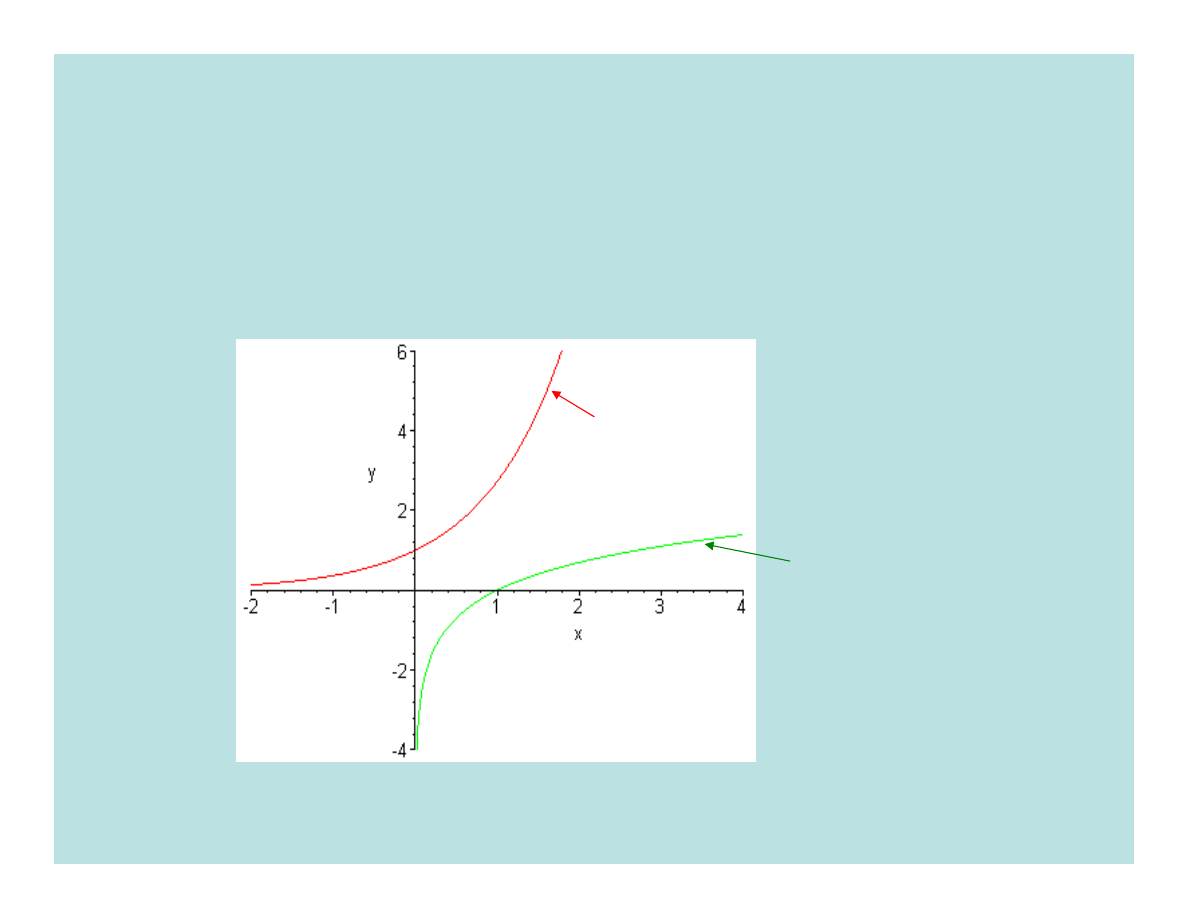
Wykresy funkcji y=e
x
oraz y=lnx
lnx
y =
x
e
y =
Wykresy funkcji y=e
x
oraz y=lnx
12
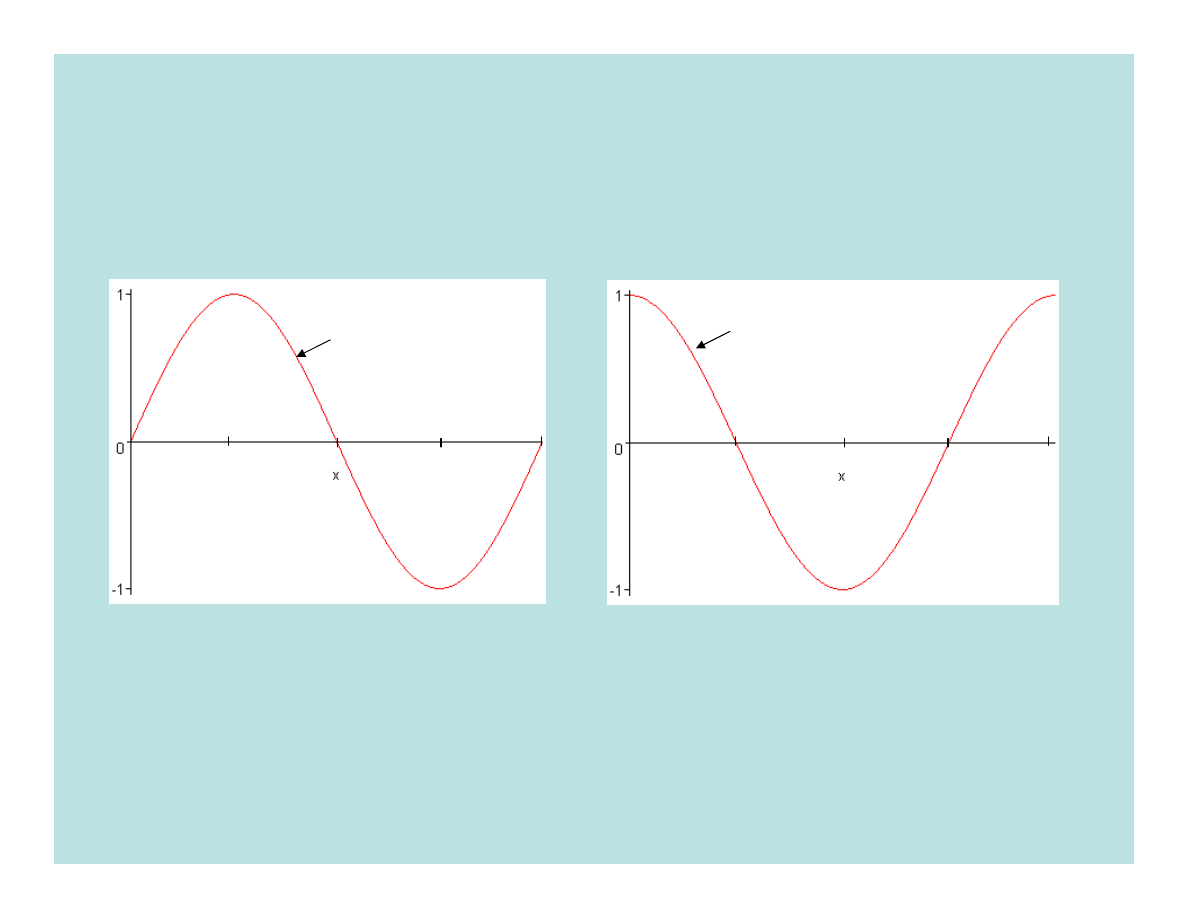
Do funkcji trygonometrycznych zaliczamy funkcje:
y
=sinx,
y=cosx
,
y
=tgx
i
y
=ctgx
. Wykresy funkcji:
7. Funkcje trygonometryczne
y
=sin
x
π/2
π
3/2π
2π
π/2
π
3/2π
2π
y
=cos
x
13
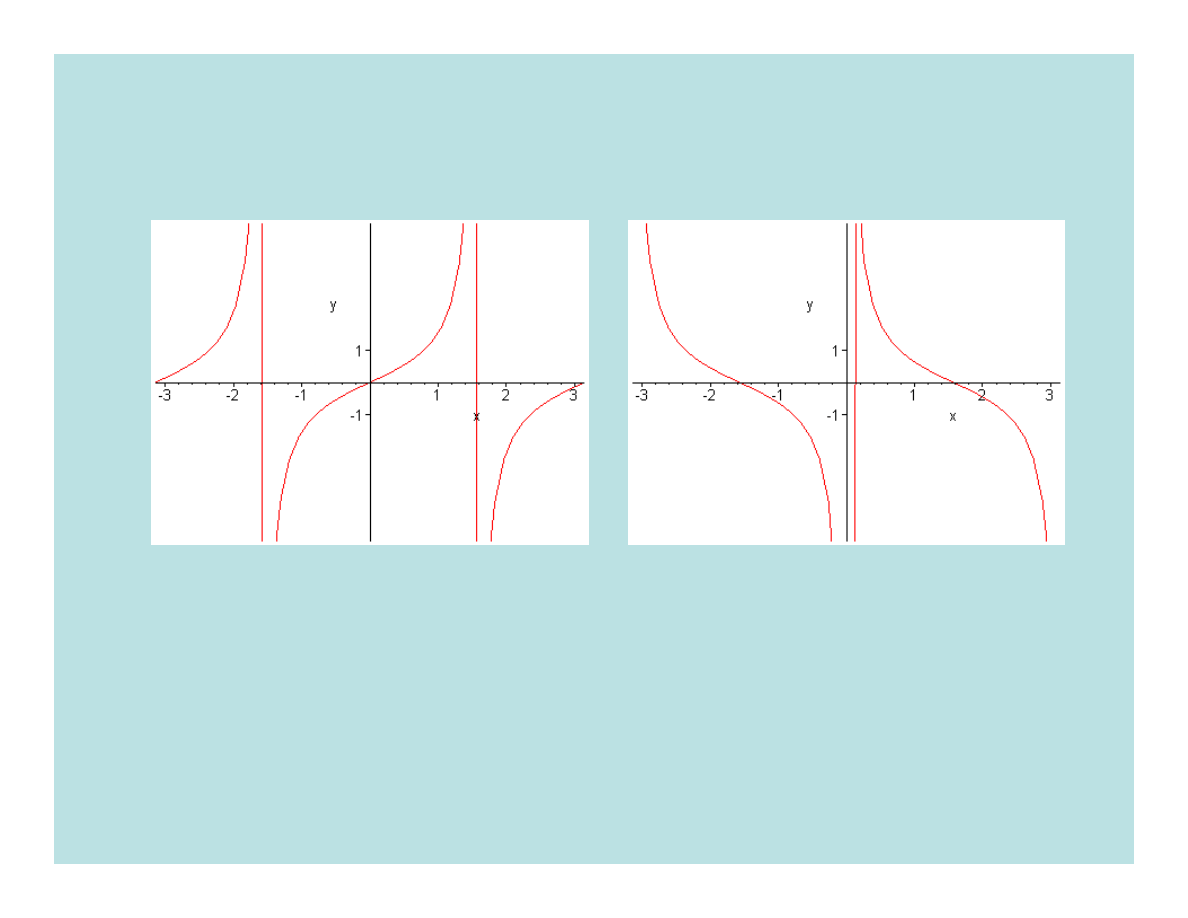
y
=tg
x
y
=ctgx
14
Funkcje trygonometryczne posiadają funkcje odwrotne
jedynie w pewnych przedziałach, w których są
różnowartościowe.
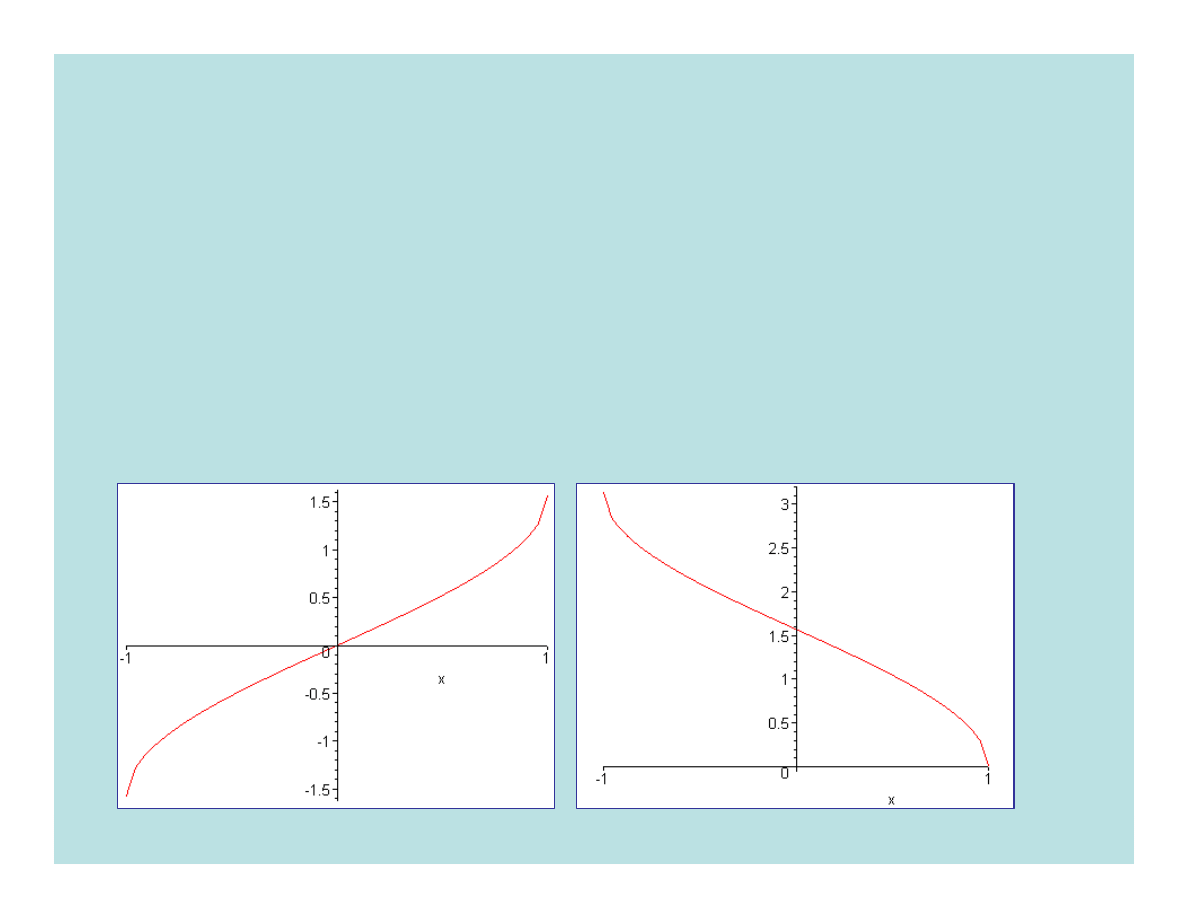
8. Funkcje cyklometryczne
y=arcsinx
y=arccosx
Funkcje odwrotne do funkcji:
y
=sinx,
y
=cosx
,
y
=tgx,
y
=ctgx
nazywamy odpowiednio:
y
=arcsinx, y=arccosx
,
y
=arctgx
i
y
=arcctgx.
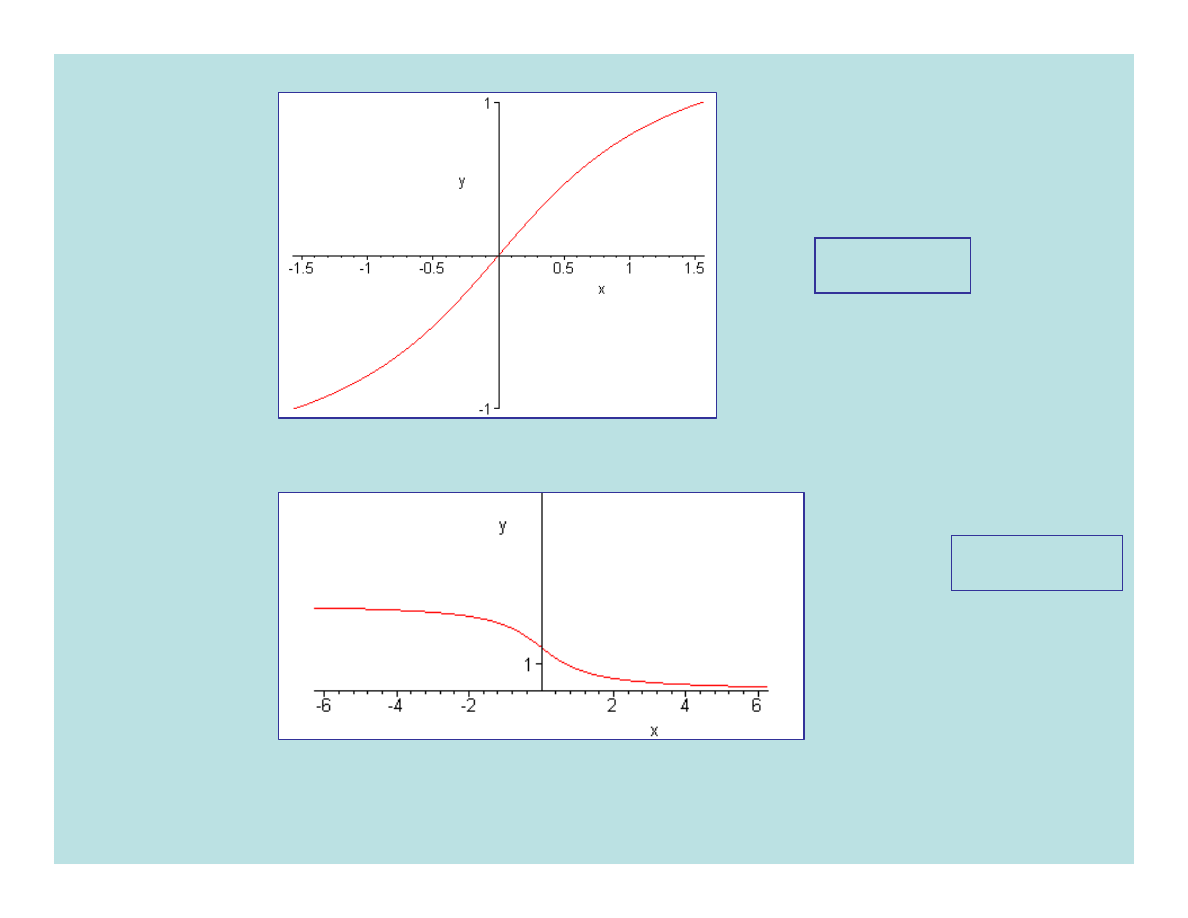
15
y=arctgx
y=arcctgx