MECHANIKA TEORETYCZNA

Temat nr 1

Rachunek wektorowy

1

2

Informacje organizacyjne

dr inż.

Maciej Przychodzki

A. Pokój: 304 (BL)
B. Konsultacje: poniedziałek 8:00-9:30
C. Telefon: [phone]
D. E-mail: [e-mail]
E. www: www.zmb.put.poznan.pl

Zasady zaliczenia przedmiotu

1. Ćwiczenia audytoryjne

Podstawą oceny końcowej są oceny otrzymane z dwóch kolokwiów. Oba kolokwia
muszą być zaliczone na ocenę pozytywną. W przypadku niezaliczenia kolokwium w
pierwszym terminie student może skorzystać z drugiego terminu. Otrzymanie ocen
niedostatecznych z kolokwium w pierwszym i drugim terminie skutkuje oceną
niedostateczną z zaliczenia. Wówczas student może przystąpić do kolokwium
poprawkowego z zakresu materiału, którego nie zaliczył. W przypadku niezaliczenia
kolokwium poprawkowego konieczne jest powtórzenie przedmiotu w następnym roku
akademickim.
Ponadto przy wystawianiu oceny końcowej będą wzięte pod uwagę oceny z bieżącej
kontroli wiedzy (np. odpowiedzi przy tablicy).
UWAGA:
Zaliczenie komisyjne może zarządzić Dyrektor IKB na wniosek studenta, jeżeli w
uzasadnieniu wniosku student wykaże, iż został potraktowany niesprawiedliwie.

3

2. Ćwiczenia projektowe

Ocena ćwiczeń projektowych jest wystawiana na podstawie ocen z pięciu zadań
przeznaczonych do samodzielnego wykonania oraz ocen z obron tych zadań.
Ocenę bardzo dobrą za pojedyncze zadanie projektowe można otrzymać, jeżeli
zadanie wykonane poprawnie i zgodnie z ustalonymi zasadami zostanie oddane w
terminie. Jeżeli zadanie będzie wykonane niepoprawnie lub niestarannie, wówczas
podlega ono zwrotowi do poprawienia, a ocena jest odpowiednio obniżona. Jeżeli
zadanie nie zostanie oddane w ciągu trzech tygodni od ustalonego terminu, to
wówczas jest ono ocenione na ocenę niedostateczną. Otrzymanie jednej oceny
niedostatecznej z zadania projektowego powoduje, że ocena z zaliczenia ćwiczeń
projektowych również jest oceną niedostateczną, a ocena poprawkowa jest ustalana
na podstawie pozostałych pozytywnych ocen z zadań. Jeżeli student otrzyma więcej niż
jedną ocenę niedostateczną z zadań projektowych, to wówczas zajęcia nie zostają
zaliczone i należy je powtórzyć w kolejnym roku akademickim.
Po oddaniu każdego ćwiczenia projektowego w wyznaczonym terminie będzie mieć
miejsce jego obrona w formie pisemnej. W przypadku niezaliczenia obrony przysługuje
jeden termin poprawkowy. Otrzymanie jednej oceny niedostatecznej w terminie
poprawkowym skutkuje oceną niedostateczną z zaliczenia zajęć projektowych , a
ocena poprawkowa jest ustalana na podstawie pozostałych pozytywnych ocen. Jeżeli
student otrzyma więcej niż jedną ocenę niedostateczną z obrony w terminie
poprawkowym, to wówczas zajęcia nie zostają zaliczone i należy je powtórzyć w
kolejnym roku akademickim.

4

5

Formularze ćwiczeń projektowych należy pobrać ze strony internetowej:

www.zmb.put.poznan.pl

Zakładka: studenci → formularze → studia stacjonarne → mechanika teoretyczna

6

3. Zasady wykonywania zadań projektowych

A. Rozwiązanie na kartkach formatu A4 zapisane jednostronnie.
B. Rysunek do zadania na pierwszej stronie ze wszystkimi danymi, wykonany

ołówkiem i od linijki.

C. Obliczenia zapisane starannie, czytelnie i bez skreśleń długopisem lub ołówkiem

(nie używać koloru czerwonego).

D. Kolejność zapisu obliczeń:

1 – wzór

2 – pełne podstawienie (bez obliczeń pośrednich)

3 – wynik.

E. Jednostki przy wszystkich wielkościach mianowanych w wyniku (Nie zapisywać

jednostek pośrednich).

F. Wykresy, schematy i rysunki pomocnicze wykonywać starannie ołówkiem używając

przyborów do kreślenia (linijka, cyrkiel). Na wykresach podać jednostki.

G. Kartki pojedyncze, równo przycięte spiąć spinaczem do papieru (nie zszywać!) lub

włożyć w koszulkę foliową.

Rachunek wektorowy

7

1. Pojęcie skalara i wektora

– wielkość, którą można określić za pomocą jednej liczby rzeczywistej.

Np.: masa, temperatura, czas, praca, energia.

Skalar

Wektor – wielkość, którą określa wartość, kierunek i zwrot w przestrzeni.

Np.: siła, prędkość, przyspieszenie.

Oznaczenia wektorów:

AB

a

a

,

,

,



a

Wartość bezwzględna wektora - moduł:

a

AB

a

,

,

,



a

8

2. Podział wektorów

Wektor związany z punktem (uczepiony)
Do jego określenia potrzebna jest linia działania, moduł, zwrot i położenie
początku wektora.

Wektor związany z prostą (posuwny, ślizgający się)
Do jego określenia potrzebna jest linia działania, moduł i zwrot. Wektor ten
można przesuwać wzdłuż linii działania.

Wektor swobodny
Do jego określenia potrzebny jest moduł, zwrot i kierunek równoległy do linii
działania. Wektor ten nie ma ściśle określonego miejsca w przestrzeni.

Wektor zerowy
Wektor, którego moduł jest równy zeru.

9

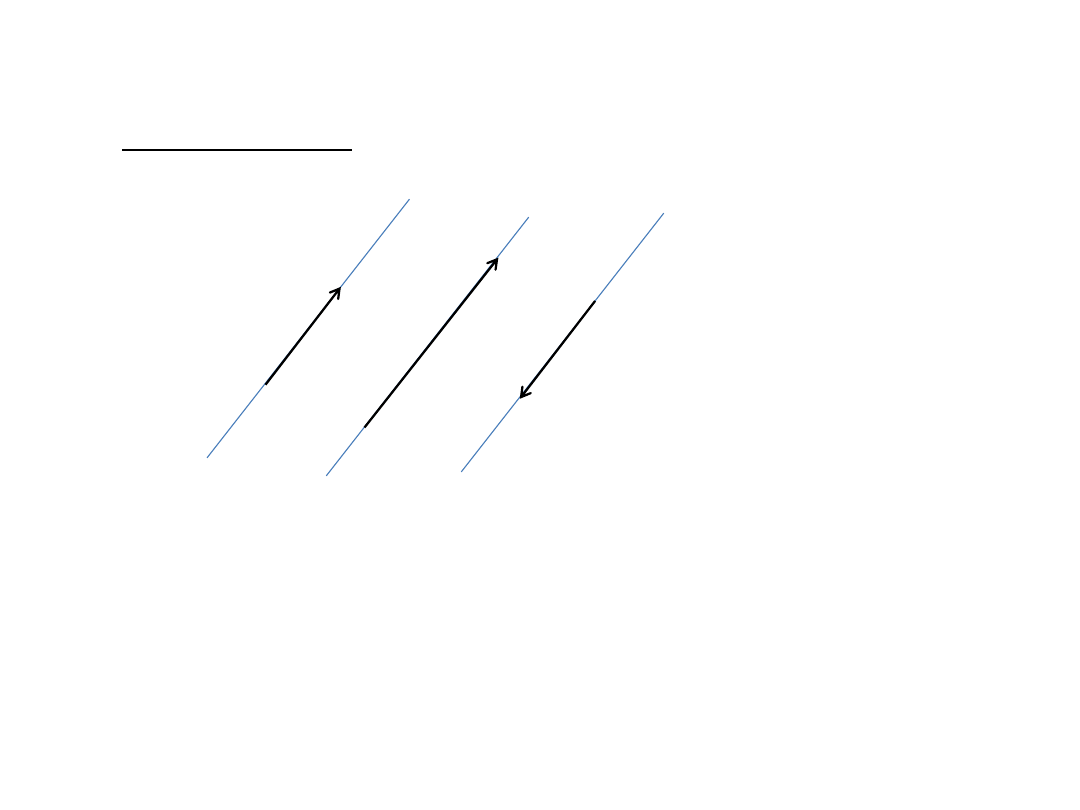
3. Relacje wektorów

Wektory równoległe - mają ten sam kierunek w przestrzeni.

a



b



c



10

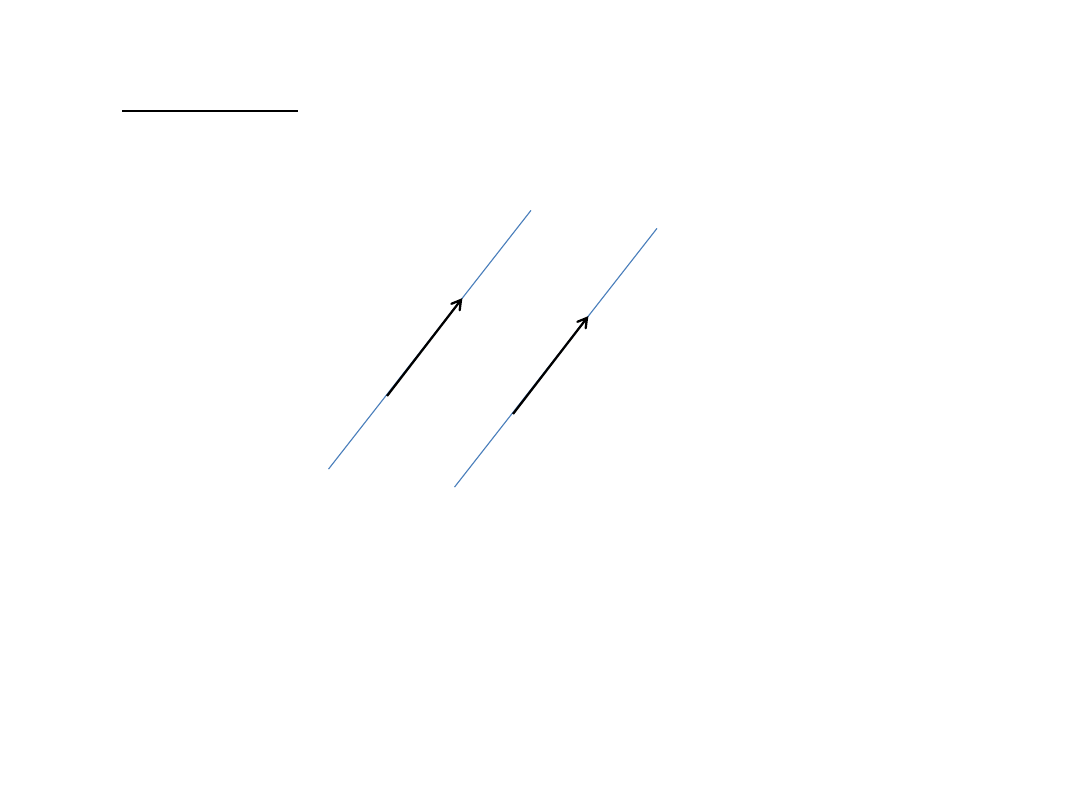
Wektory równe - wektory równoległe, które mają równe moduły i te same
zwroty.

a



b



11

Wektory przeciwne - wektory równoległe, które mają równe moduły i przeciwne
zwroty.

a



b



12

Wektory równoważne - wektory równe, które mają wspólną linię działania.

a



b



Wersor (wektor jednostkowy) wektora a – wektor, którego kierunek jest taki sam
jak kierunek wektora a, natomiast jego moduł jest równy jedności.

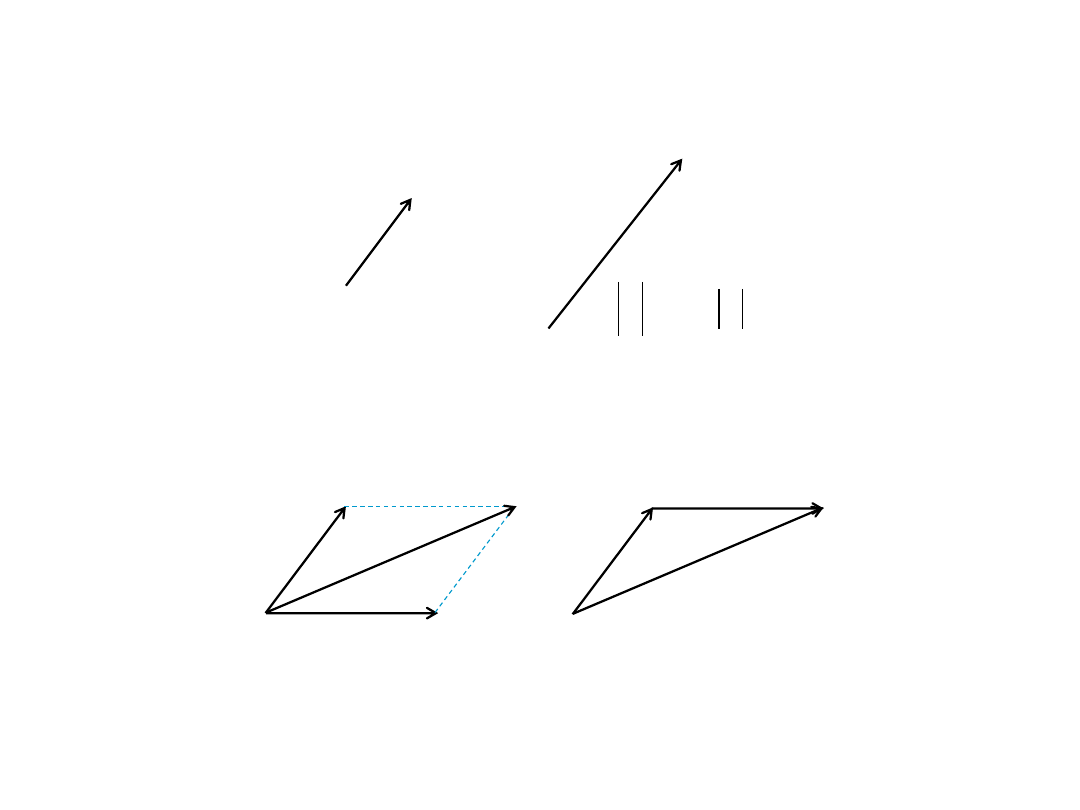
13

4. Mnożenie wektora przez skalar

a



a

b











a

b











5. Graficzne dodawanie wektorów

a



b



c



a



b



c



b

a

c











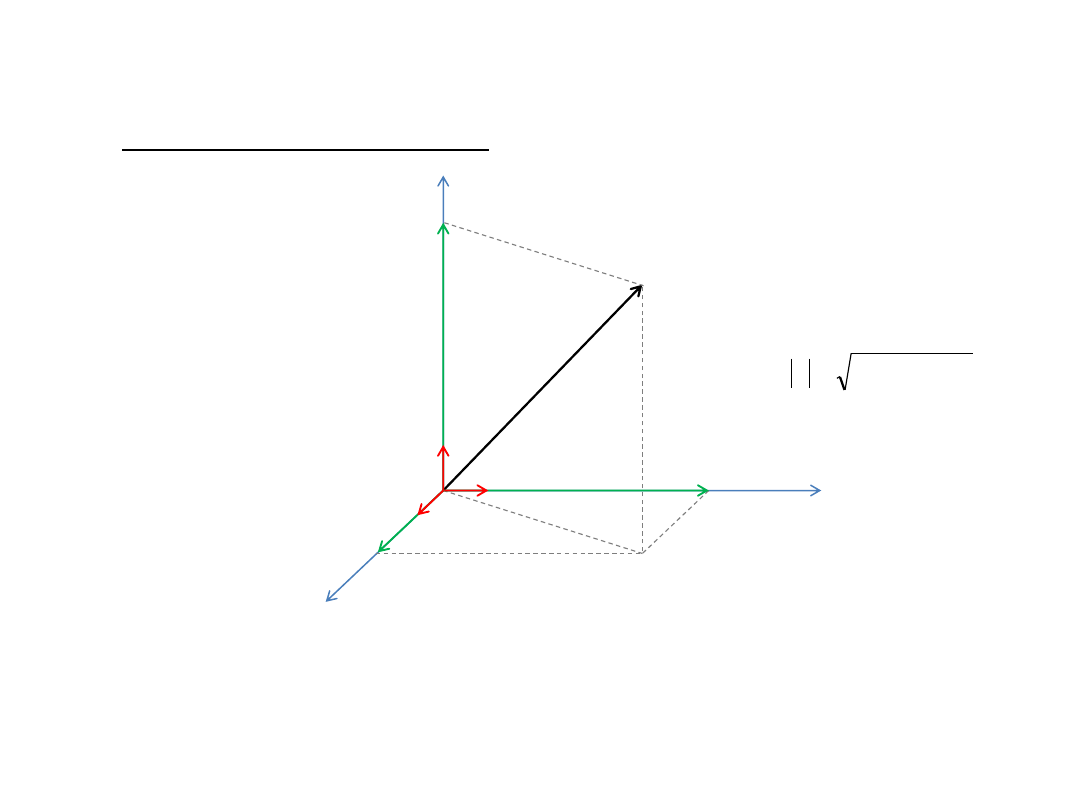
14

6. Analityczne przedstawienie wektora

Kartezjański układ współrzędnych

1

, e

i





1

, x

x

2

, x

y

2

, e

j





3

, e

k





3

, x

z

1

, a

a

x





2

, a

a

y





3

, a

a

z





a















































3

2

1

a

a

a

a

a

a

a

z

y

x



z

y

x

a

a

a

a















k

a

a

j

a

a

i

a

a

z

z

y

y

x

x



















k

a

j

a

i

a

a

z

y

x



























3

1

3

3

2

2

1

1

i

i

i

e

a

e

a

e

a

e

a

a











2

2

2

z

y

x

a

a

a

a









Moduł wektora:

15

7. Analityczne dodawanie wektorów

 

b

a

ab

b

a









,

cos





8. Iloczyn skalarny wektorów

Iloczyn skalarny dwóch wektorów jest to skalar równy iloczynowi modułów
wektorów składowych przez cosinus kata zawartego między nimi



 















k

c

j

c

i

c

k

b

a

j

b

a

i

b

a

k

b

j

b

i

b

k

a

j

a

i

a

b

a

c

z

y

x

z

z

y

y

x

x

z

y

x

z

y

x



































































z

z

y

y

x

x

b

a

b

a

b

a

b

a













 

ab

b

a

b

a

b

a

b

a

z

z

y

y

x

x











,

cos

Cosinusy kierunkowe:

 

a

a

i

a

i

a

x

a

x



















,

cos

 

a

a

j

a

j

a

y

a

y



















,

cos

 

a

a

k

a

k

a

z

a

z



















,

cos

16

9. Iloczyn wektorowy wektorów

Iloczyn wektorowy dwóch wektorów jest to wektor, którego moduł równa się
iloczynowi modułów wektorów składowych przez sinus kąta zawartego między nimi

 

b

a

ab

c

b

a

c











,

sin







a



b



c





UWAGA:
Iloczyn wektorowy nie spełnia prawa przemienności.

17













k

c

j

c

i

c

k

b

a

b

a

j

b

a

b

a

i

b

a

b

a

b

a

c

z

y

x

x

y

y

x

z

x

x

z

y

z

z

y











































z

y

x

z

y

x

b

b

b

a

a

a

k

j

i

b

a

c



















10. Iloczyn mieszany wektorów

 

d

c

b

a

c

b

a

c





























18

Zadanie 1

Dane są wektory:

k

j

i

a









5

3







k

j

i

b









6

4







k

j

i

c









7

2

2







k

j

i

d









4

4

3







c) znaleźć kąty między wektorami: ,

 

 

       

d

c

d

b

c

b

d

a

c

a

b

a

























,

,

,

,

,

,

,

,

,

,

,

b) określić wektor oraz jego cosinusy kierunkowe,

c

b

a

e









4

3

2







a) obliczyć sumę wektorów oraz znaleźć kąty, jakie wektor tworzy
z osiami układu współrzędnych x, y, z,

c

b

a

e















e



d) znaleźć iloczyny mieszane: .

 





   

b

a

d

d

b

c

c

a

b

c

b

a









































,

,

,

19

Odpowiedzi do zadania 1

k

j

i

e









18

4

7







a)

723

,

19

389





e



 

 

3

1

69

,

3549

,

0

723

,

19

7

,

cos













i

e

i

e









 

 

8

1

78

,

2028

,

0

723

,

19

4

,

cos













j

e

j

e









 

 

3

8

24

,

9126

,

0

723

,

19

18

,

cos













k

e

k

e









20

j

i

e







5

6





b)

810

,

7

61





e



 

7682

,

0

81

,

7

6

,

cos





i

e





 

6402

,

0

81

,

7

5

,

cos





j

e





 

0

,

0

81

,

7

0

,

cos





k

e





21

c)

 

 

8

5

43

,

7197

,

0

28

,

7

916

,

5

31

,

cos



















b

a

ab

b

a

b

a













 

 

0

4

15

,

9628

,

0

549

,

7

916

,

5

43

,

cos



















c

a

ac

c

a

c

a













 

 

3

1

33

,

8366

,

0

071

,

7

916

,

5

35

,

cos



















d

a

ad

d

a

d

a













 

 

8

29

,

8734

,

0

549

,

7

28

,

7

48

,

cos



















b

a

bc

c

b

c

b













 

 

4

3

51

,

6216

,

0

071

,

7

28

,

7

32

,

cos



















d

b

bd

d

b

d

b













 

 

7

38

,

7868

,

0

071

,

7

549

,

7

42

,

cos



















d

c

cd

d

c

d

c













22

d)

 

17









c

b

a











17







c

a

b







 

81







d

b

c







 

73







b

a

d





