PODSTAWY EKONOMETRII

dr Dariusz Karaś

1

ESTYMACJA PARAMETRÓW STRUKTURALNYCH JEDNORÓWNANIOWEGO LINIOWEGO MODELU

EKONOMETRYCZNEGO

Definicja

Estymacja (tj. szacowanie) parametrów strukturalnych modelu ekonometrycznego oznacza
znalezienie ocen parametrów strukturalnych na podstawie konkretnej próby (sprowadza się do
przypisywania nieokreślonym liczbowo parametrom konkretnych wartości liczbowych). Szacowanie
to powinno być przeprowadzone w taki sposób, aby zapewniło najlepsze dopasowanie modelu do
danych empirycznych.

Metoda

Powszechnie wykorzystywaną metodą szacowana parametrów strukturalnych liniowych modeli
ekonometrycznych jest klasyczna metoda najmniejszych kwadratów (KMNK).

Twierdzenie Gaussa-Markowa

W klasycznym modelu regresji liniowej najlepszym nieobciążonym estymatorem liniowym
parametrów jest estymator uzyskany Metodą Najmniejszych Kwadratów (MNK). Idea MNK:
minimalizuje sumę kwadratów odchyleń (reszt).

Własności estymatorów

Nieobciążoność – g jest nieobciążonym estymatorem θ, jeżeli E(g)= θ, to znaczy, gdy wartość
oczekiwana w rozkładzie z próby g jest równa θ.

Oznacza to, że gdybyśmy obliczali wartość g dla każdej z prób, którymi dysponujemy i powtarzali ten
proces nieskończenie wiele razy, to średnia z uzyskanych ocen byłaby równa θ.

Efektywność – estymator jest efektywny, jeżeli wartości g wyliczone dla różnych prób nie różnią się
między sobą znacznie tzn. jeżeli wariancja estymatorów jest mała. Estymator z najmniejszą wariancją
to estymator najbardziej efektywny.

Zgodność – (własność dużych prób) zwiększanie liczebności próby umożliwia uzyskiwanie estymatora
o wartości coraz bliższej szacowanego parametru, z prawdopodobieństwem bliskim jedności:

i

Można wykazać, że estymator oszacowany Klasyczną Metoda Najmniejszych Kwadratów jest:

nieobciążony

zgodny

najbardziej efektywny w klasie estymatorów nieobciążonych,

czyli: BLUE –Best Linear Unbiased Estimator (najlepszy liniowy neobciążony estymator).

PODSTAWY EKONOMETRII

dr Dariusz Karaś

2

Warunki stosowalności KMNK

1) liczba obserwacji musi być większa niż liczba szacowanych parametrów,

2) rząd macierzy zmiennych objaśniających X musi być równy liczbie szacowanych parametrów
(warunek ten oznacza brak wspóliniowości zmiennych, tzn. że zmienne objaśniające są liniowo
niezależne, czyli nie tworzą ze sobą takiej kombinacji liniowej, która w wyniku daje wektor zerowy),

3) postać modelu jest liniowa względem parametrów (lub sprowadzalna do liniowej),

4) wartość oczekiwana składnika losowego jest równa 0,

5) wariancja składnika losowego jest jednakowa dla wszystkich obserwacji (homoskedastyczność),

6) nie występuje autokorelacja składników losowych - składniki losowe dla różnych obserwacji nie
zależą od siebie,

7) zmienne objaśniające są nielosowe - nie zalezą od składnika losowego,

8) składnik losowy dla każdej obserwacji ma rozkład normalny.

Jeżeli nie są spełnione założenia 1) - 2), nie można zastosować matematycznych formuł na KMNK.

Jeżeli nie są spełnione założenia 4) - 7), to estymator KMNK nie jest efektywny.

Założenie 8) nie ma znaczenia dla własności estymatora KMNK. Jego spełnienie jest konieczne, aby
można było zastosować testy statystyczne pozwalające sprawdzić pozostałe założenia (większość
testów statystycznych bazuje na założeniu, że zmienna losowa ma rozkład normalny).

Estymator KMNK:

PODSTAWY EKONOMETRII

dr Dariusz Karaś

3

Procedura estymacji KMNK

Sposób I (krok po kroku)

1) zapisanie macierzy zmiennych X i Y

2) zapisanie macierzy transponowanej

3) wyznaczenie macierzy Hessa

4) wyznaczenie macierzy

5) obliczenie wyznacznika macierzy Hessa

6) wyznaczenie macierzy odwrotnej do macierzy Hessa

7) wyznaczenie wektora ocen parametrów strukturalnych modelu

8) zapis modelu w postaci empirycznej (zapisanie modelu z odpowiednimi wartościami ocen
parametrów)

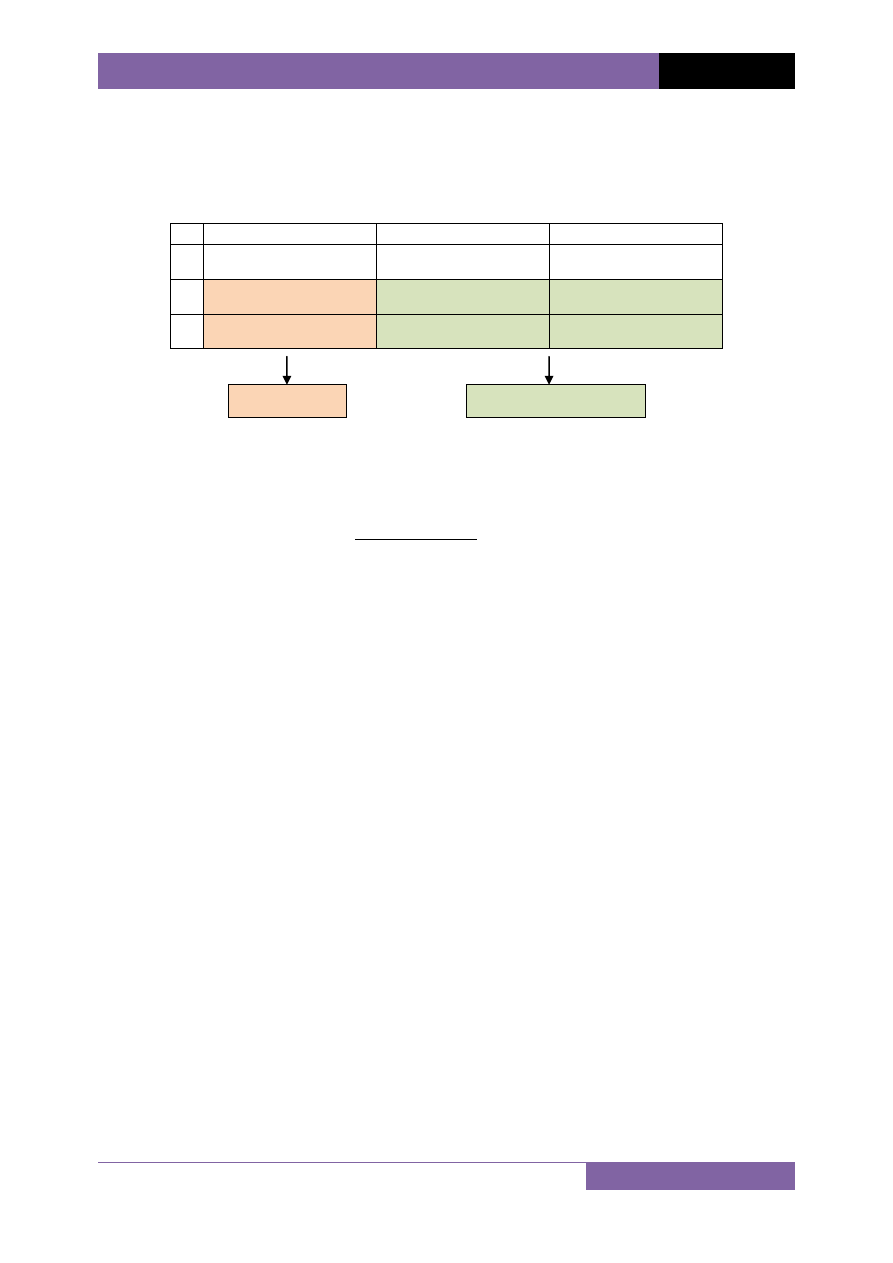
PODSTAWY EKONOMETRII

dr Dariusz Karaś

4

Sposób II (tabela Cross - przypadek dla modelu z jedną zmienną objaśniającą)

1) utworzenie tabeli

Y

1

X

Y

1

n

X

2) odwrócenie macierzy Hessa

3) wyznaczenie wektora ocen parametrów strukturalnych modelu

4) zapis modelu w postaci empirycznej

wektor

macierz Hessa

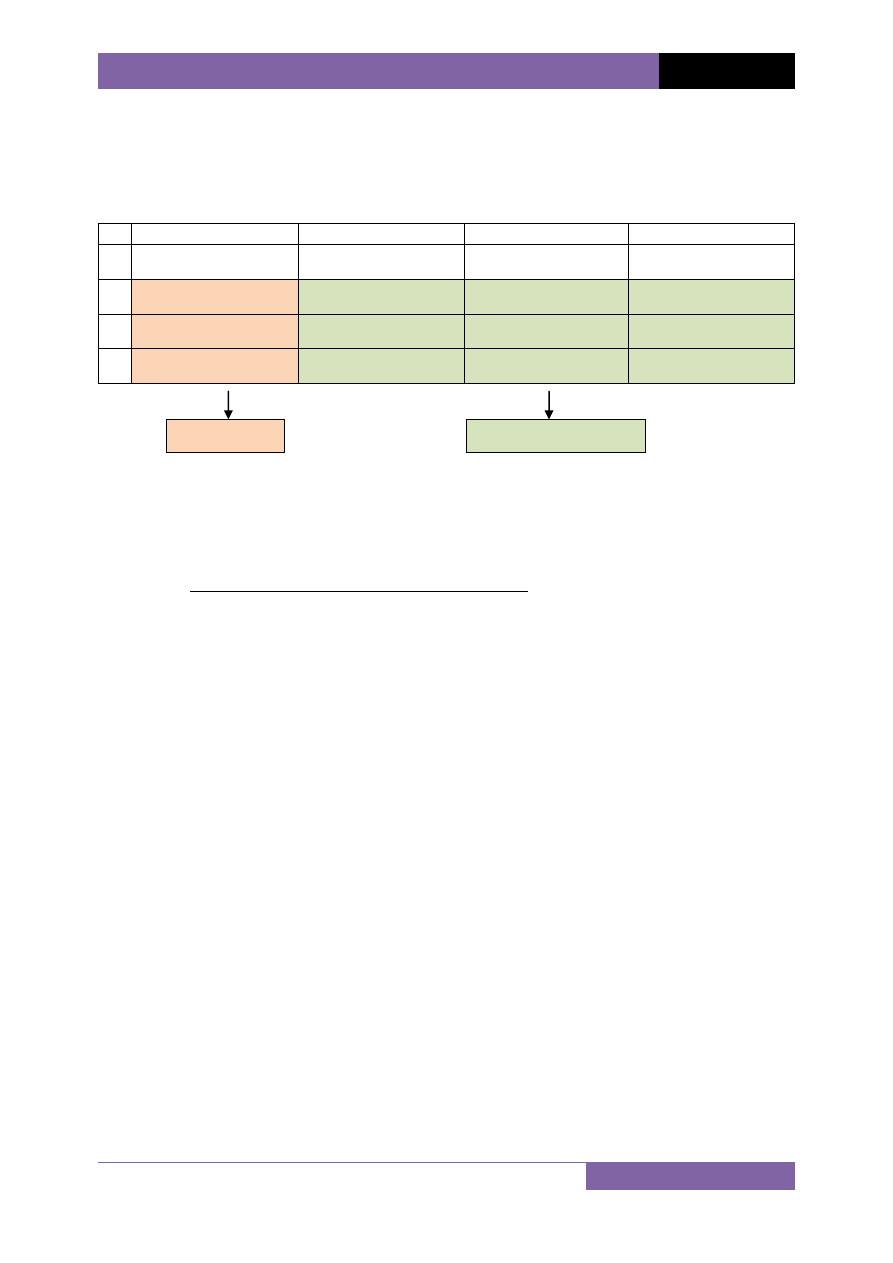
PODSTAWY EKONOMETRII

dr Dariusz Karaś

5

Sposób II (tabela Cross - przypadek dla modelu z dwiema zmiennymi objaśniającymi)

1) utworzenie tabeli

Y

1

X1

X2

Y

1

n

X1

X2

2) odwrócenie macierzy Hessa

3) wyznaczenie wektora ocen parametrów strukturalnych modelu

4) zapis modelu w postaci empirycznej

wektor

macierz Hessa

PODSTAWY EKONOMETRII

dr Dariusz Karaś

6

Interpretacja ocen parametrów strukturalnych modelu

- wyraz wolny, bez interpretacji

- wraz ze wzrostem zmiennej objaśniającej o jedną jednostkę, zmienna objaśniana zmieni się (tj.

wzrośnie/zmaleje) o

jednostek, przy pozostałych czynnikach niezmienionych (ceteris paribus).

Każdy parametr interpretuje się osobno.