Instytut Automatyzacji Procesów Technologicznych

i Zintegrowanych Systemów Wytwarzania

LABORATORIUM

Drgania układów fizycznych,

Drgania mechaniczne

BADANIE DRGAŃ DYSKRETNEGO UKŁADU

O DWÓCH STOPNIACH SWOBODY

2

1. CEL ĆWICZENIA I ZAKRES BADAŃ

Dyskretny układ drgający o dwóch stopniach swobody jest najprostszym modelem, na którym można

wykonać badania eksperymentalne oraz zaobserwować i z pewnym, nieuniknionym błędem wyznaczyć
specyficzne własnośći układu i jego ruchu drgającego, o podstawowym znaczeniu w procesie
projektowania nowych obiektów technicznych oraz modyfikacji konstrukcji obiektów już istniejących.

Podstawowym celem ćwiczenia jest doświadczalne potwierdzenie modeli i rozważań teoretycznych

przedstawionych w kolejnym podrozdziale i pełniejsze zrozumienie zjawisk towarzyszących drganiom
mechanicznym – wibracjom, które w znacznym zakresie można uogólnić dla drgań układów ciągłych.

Zakres badań obejmuje wyznaczenie postaci (modów) drgań, obliczenie naturalnych częstości drgań

oraz porównanie ich wartości z wyznaczonymi w eksperymencie. Należy porównać postacie drgań
wzbudzonych warunkami początkowymi odpowiadajacymi obliczonym wektorom własnym układu
z postaciami drgań wzbudzonymi warunkami początkowymi różniącymi się od opisanych wektorami
własnymi.

1.1. Wstęp teoretyczny

Równania drgań dyskretnych układów mechanicznych można wyznaczyć stosując zasadę

d’Alemberta. W przypadku układów o wielu stopniach swobody korzystniejsze jest posługiwanie się
równaniem Lagrange’a II rodzaju. Jeśli równania ruchu wyznaczane są dla współrzędnych odmierzanych
w układzie bezwzględnym, z czym mamy w praktyce najczęściej do czynienia, najwygodniej jest przyjąć
zapis macierzowy, w którym macierze tworzone są bezpośrednio na podstawie schematu układu
drgającego. Do wniosków takich można dojść śledząc analizę przeprowadzoną dla modelu układu
o dwóch stopniach swobody.

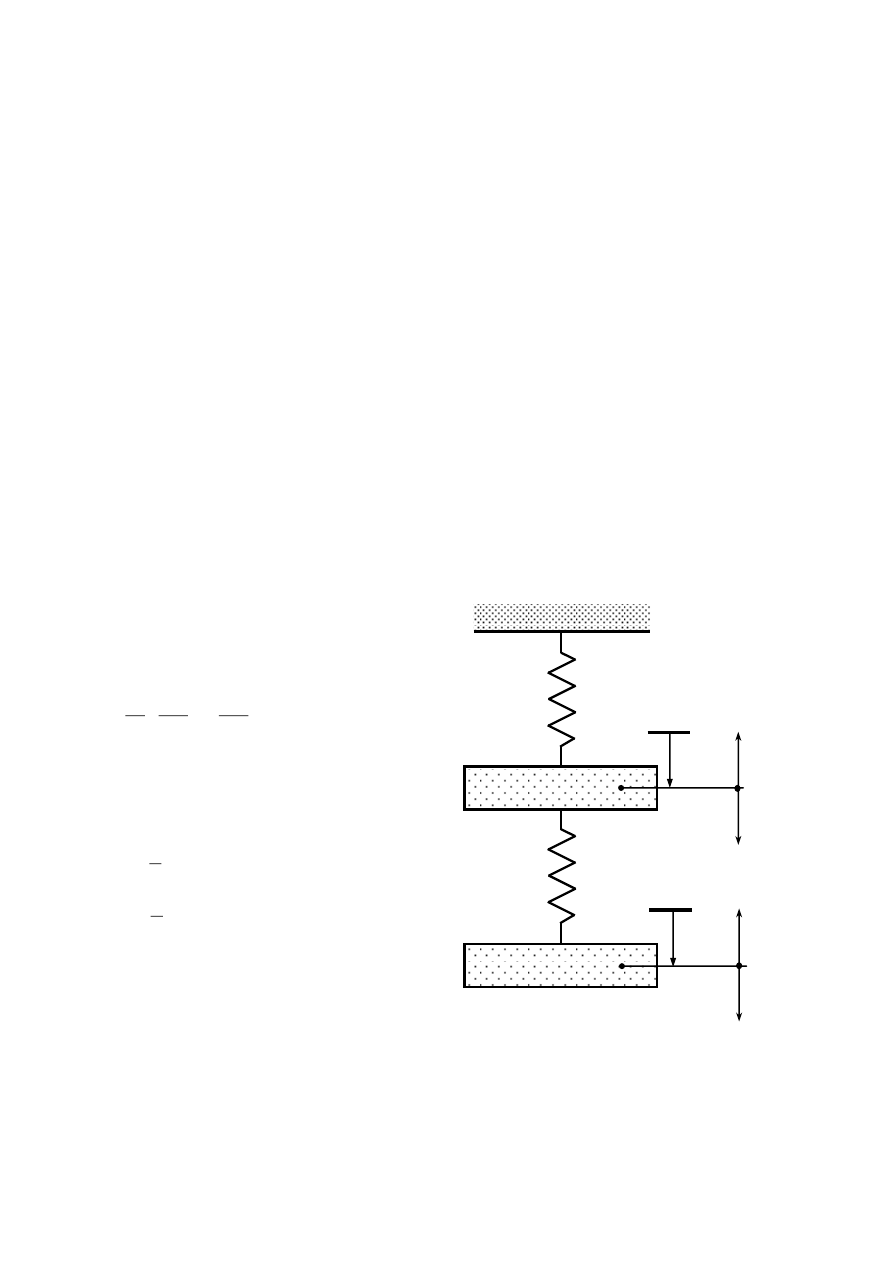
Do utworzenia równań ruchu drgającego na

kierunku pionowym mas m

1

oraz m

2

, rys. 4.1,

zastosowane będzie równanie Lagrange’a II
rodzaju

0

























i

i

q

U

q

E

dt

d



,

,

2

,

1



i

gdzie:

,

)

(

1

1

1

x

t

x

q





,

)

(

2

2

2

x

t

x

q









2

2

2

2

1

1

2

1

x

m

x

m

E









,









2

2

1

2

2

1

1

2

1

x

x

k

x

k

U







.

Współrzędne x

1

oraz x

2

są odmierzane

w układzie

bezwzględnym.

W

zapisie

uporządkowanym, ze względu na współrzędne
ruchu oraz ich pochodne, różniczkowe równania
ruchu przyjmują następującą formę

Rys. 4.1. Model układu o dwóch stopniach swobody

,

0

)

(

0

,

0

)

(

)

(

0

2

2

1

2

2

2

1

2

2

1

2

1

2

1

1



























x

k

x

k

x

m

x

x

k

x

k

k

x

x

m

















(4.1)

która w zapisie macierzowym ma postać

m

1

m

2

k

1

k

2

x

1 stat.

x

2 stat.

x

1

(t)

x

2

(t)

3

.

0

0

)

(

0

0

2

1

2

2

2

2

1

2

1

2

1







































































x

x

k

k

k

k

k

x

x

m

m









(4.2)

Gdy masy więzi sprężystych są pomijalnie małe w stosunku do mas dyskretnego modelu, to statyczne

ugięcia, można obliczyć następująco

.

,

2

2

1

2

1

.

2

1

2

1

.

1

k

g

m

k

g

m

g

m

x

k

g

m

g

m

x

stat

stat











(4.3)

Rozwiązaniem różniczkowych równań ruchu drgającego (4.1) są funkcje harmoniczne, które w

ogólnym przypadku można przyjąć w postaci

,

sin

2

,

1

2

,

1

t

a

x

o





(4.4)

gdzie a

1,2

są stałymi, które wyznacza się po obliczeniu naturalnych częstotliwości ω

o1,2

. Ponieważ drugie

pochodne podług czasu t funkcji (4.4) są równe

,

sin

2

,

1

2

2

,

1

t

a

x

o

o









(4.5)

to równanie macierzowe (4.2) można przekształcić do układu równań algebraicznych (4.6)

   





   

,

0

2









X

K

M

o

(4.6)

które po prostych operacjach przyjmują postać

 

 





   

,

0

2







X

E

H

o

(4.7)

gdzie:

 















2

1

0

0

m

m

M

- macierz mas,

 





















2

2

2

2

1

)

(

k

k

k

k

k

K

- macierz sztywności,

 















2

1

x

x

X

- wektor przemieszczeń mas dyskretnych,

     

K

M

H

1





- macierz dynamiczna,

 















1

0

0

1

E

- macierz jednostkowa.

Wektor przemieszczeń ma niezerowe współrzędne, jeśli masom znajdującym się w położeniu

równowagi statycznej nadamy, w chwili t = 0, prędkości lub wychylenia początkowe, albo wprowadzimy
równocześnie obydwa te oddziaływania, zmieniające energię układu dyskretnego odpowiadającą
ugięciom statycznym. Po wykonaniu działania w okrągłym nawiasie równania (4.7) i przyrównaniu
wyznacznika uzyskanej macierzy do zera, co jest koniecznym warunkiem by a

1

oraz a

2

były różne od

zera

4

0

2

22

21

12

2

11











o

o

h

h

h

h

,

(4.8)

otrzymuje się następujące równanie charakterystyczne

0

)

(

12

21

22

11

2

22

11

4















h

h

h

h

h

h

o

o

.

(4.9)

Z równania charakterystycznego oblicza się wartości częstości naturalnych (własnych) drgań

swobodnych modelu układu dyskretnego, które w rozpatrywanym przypadku wynoszą

































.

2

4

,

2

4

2

1

2

1

2

1

2

1

2

2

2

1

1

1

2

2

1

1

1

2

2

1

2

1

2

1

2

1

2

2

2

1

1

1

2

2

1

1

1

1





























































m

m

m

m

k

k

m

k

k

m

k

m

k

k

m

k

m

m

m

m

k

k

m

k

k

m

k

m

k

k

m

k

o

o

(4.10)

Każdej naturalnej częstości odpowiada oddzielna postać, moda drgań, którą opisuje pojedynczy dla

każdego stopnia swobody wektor przemieszczeń. Przemieszczenia te są niezmienne, jeśli porównać je
między sobą. Ta względna stałość jest drugą po naturalnej częstości podstawową własnością drgającego
układu.

Pierwsza postać drgań jest następująca

 















21

11

1

a

a

a

,

(4.11)

przy czym drugi wskaźnik oznacza pierwszą modę drgań. Często przyjmuje się dla wygody podstawienie

1

21



a

,

(4.12)

wówczas modalną składową masy m

1

dla pierwszej mody można wyznaczyć z pierwszego równania

(4.7), które ma postać









0

21

2

11

1

2

2

1











a

k

a

m

k

k

o

,

(4.13)

skąd









1

2
01

2

1

2

21

2
01

2

1

2

11



















k

k

k

a

k

k

k

a

.

(4.14)

Podobnie dla drugiej mody otrzymuje się

 















22

12

1

a

a

a

(4.15)

a następnie dla

1

22



a

oblicza kolejno





1

2
01

2

1

2

12











k

k

k

a

.

(4.16)

5

Macierz wektorów własnych, zwana również macierzą modalną czyli macierzą postaci drgań

swobodnych dla rozważanego układu o dwóch stopniach swobody jest macierzą kwadratową

 

  



































1

1

12

11

22

21

12

11

2

1

a

a

a

a

a

a

a

a

A

(4.17)

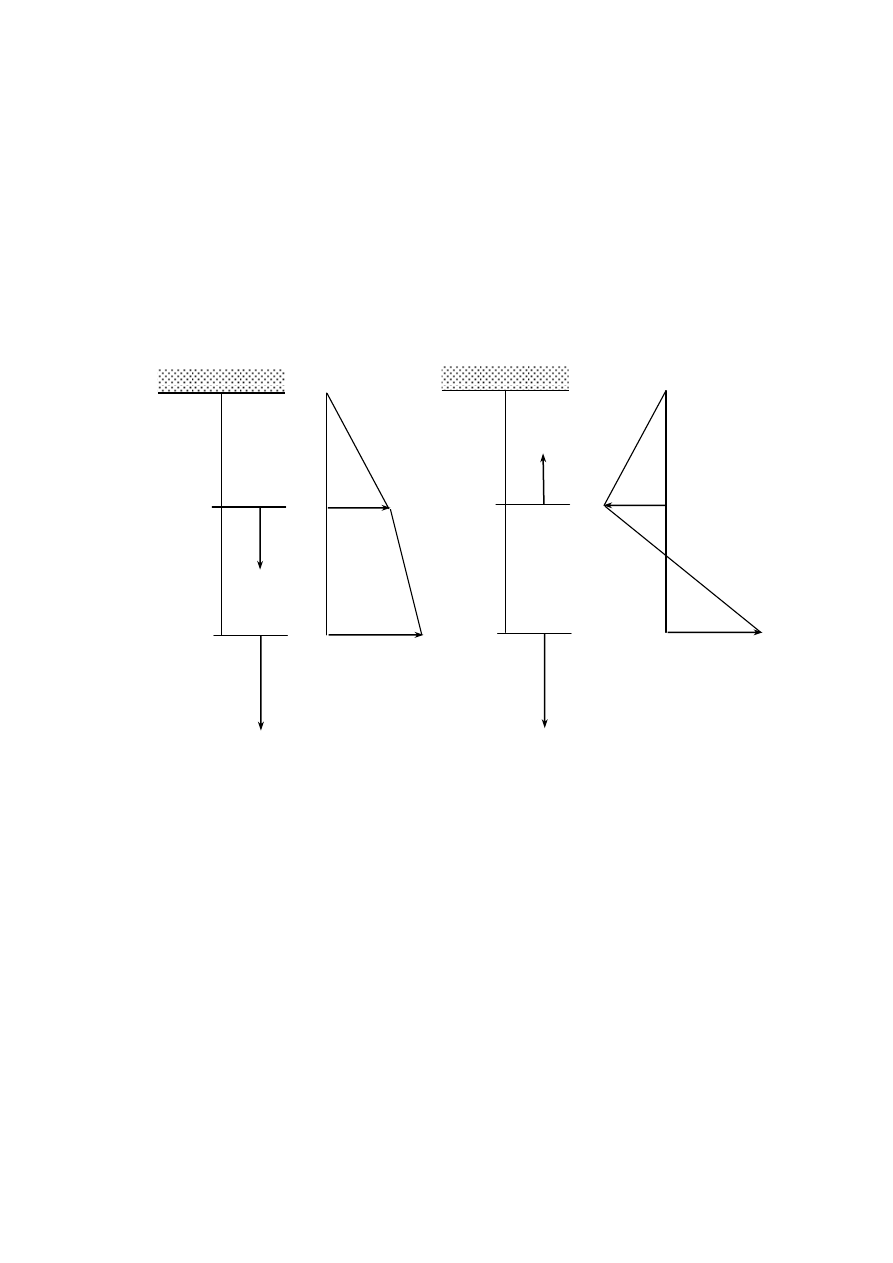
W przypadku pierwszej postaci drgań układu dwumasowego, drgania o najdłuższym okresie,

występuje współbieżny ruch mas, co odpowiada, w każdej chwili czasu, przemieszczaniu się ich w tym
samym kierunku poza chwilami, gdy równocześnie zatrzymują się. Stosunki chwilowych przemieszczeń
mas, odmierzanych względem położenia równowagi statycznej uwidoczniono na rys. 4.2a. Drugiej
postaci drgań odpowiada przeciwbieżne przemieszczanie się mas, rys. 4.2b, z prędkością kołową



o2

>



o1

.

Rys. 4.2. Postacie drgań własnych układu dwumasowego: a) pierwsza moda, b) druga moda

1.2. Ortogonalność postaci drgań własnych

Dla pierwszej i drugiej mody drgań, na podstawie równań (4.6) i (4.11) oraz (4.6) i (4.15) otrzymuje

się

 

 

 

 

0

1

1

2

1









a

K

a

M

o

,

(4.18)

 

 

 

 

0

2

2

2

2









a

K

a

M

o

,

(4.19)

Mnożąc równania (4.18) oraz (4.19) odpowiednio przez transponowane wektory własne

 

T

a

2

oraz

 

T

a

1

uzyskuje się

 

 

   

 

 

0

1

2

1

2

2

1









a

K

a

a

M

a

T

T

o

,

(4.20)

 

 

   

 

 

0

2

1

2

1

2

2









a

K

a

a

M

a

T

T

o

.

(4.21)

W dalszym ciągu zostanie transponowane człon po członie równanie (4.21), co daje

a)

b)

a

11

a

11

a

21

=1

a

21

=1

a

12

a

22

=1

a

22

=1

a

12

6

 

 

 





 

 

 

 

T

T

T

T

o

T

T

o

a

M

a

a

M

a

1

2

2

2

2

1

2

2











.

(4.22)

Ponieważ macierz mas jest symetryczna to zamiana wierszy na kolumny niczego nie zmieni, natomiast

transponowanie wektora transponowanego daje w wyniku wektor oryginalny, zatem prawa strona
równania

 

 

 

1

2

2

2

a

M

a

T

o







.

(4.23)

Podobnie, uzyskuje się po przekształceniach drugiego członu równania (4.21) wyrażenie w postaci

 

 

 

1

2

a

K

a

T

,

(4.24)

zatem transponowane równanie (4.21) jest następujące

 

 

   

 

 

0

1

2

1

2

2

2









a

K

a

a

M

a

T

T

o

.

(4.25)

Odejmując od równania (4.25) równanie (4.20) otrzymuje się





 

 

 

,

0

1

2

2

1

2

2









a

M

a

T

o

o

(4.26)

a ponieważ

2

1

o

o







to

 

 

 

,

0

1

2



a

M

a

T

(4.27)

oraz z zależności (4.25)

 

 

 

0

1

2



a

K

a

T

.

(4.28)

Ostatnie dwa równanie przedstawiają relacje ortogonalności wektorów własnych. Można to uogólnić

dla układów o wielu stopniach swobody, należy jedynie zastąpić indeksy 1 i 2 odpowiednio symbolami i
oraz j

 

 

 

,

0



i

T

j

a

M

a

j

i



,

(4.29)

 

 

 

0



i

T

j

a

K

a

.

(4.30)

Ponieważ w tym przypadku macierz modalna jest następująca

 

     

 

 





n

j

i

a

a

a

a

a

a

A

...

...

3

2

1



(4.31)

to dla układu o n – stopniach swobody warunek ortogonalności można zapisać

     



diag

A

M

A

T



,

(4.32)

oraz

     



diag

A

K

A

T



.

(4.33)

Po wykonaniu operacji skalowania wektorów postaci drgań własnych ma postać

      

E

A

M

A

sk

T

sk



,

(4.34)

oraz

      

E

A

K

A

sk

T

sk



.

(4.35)

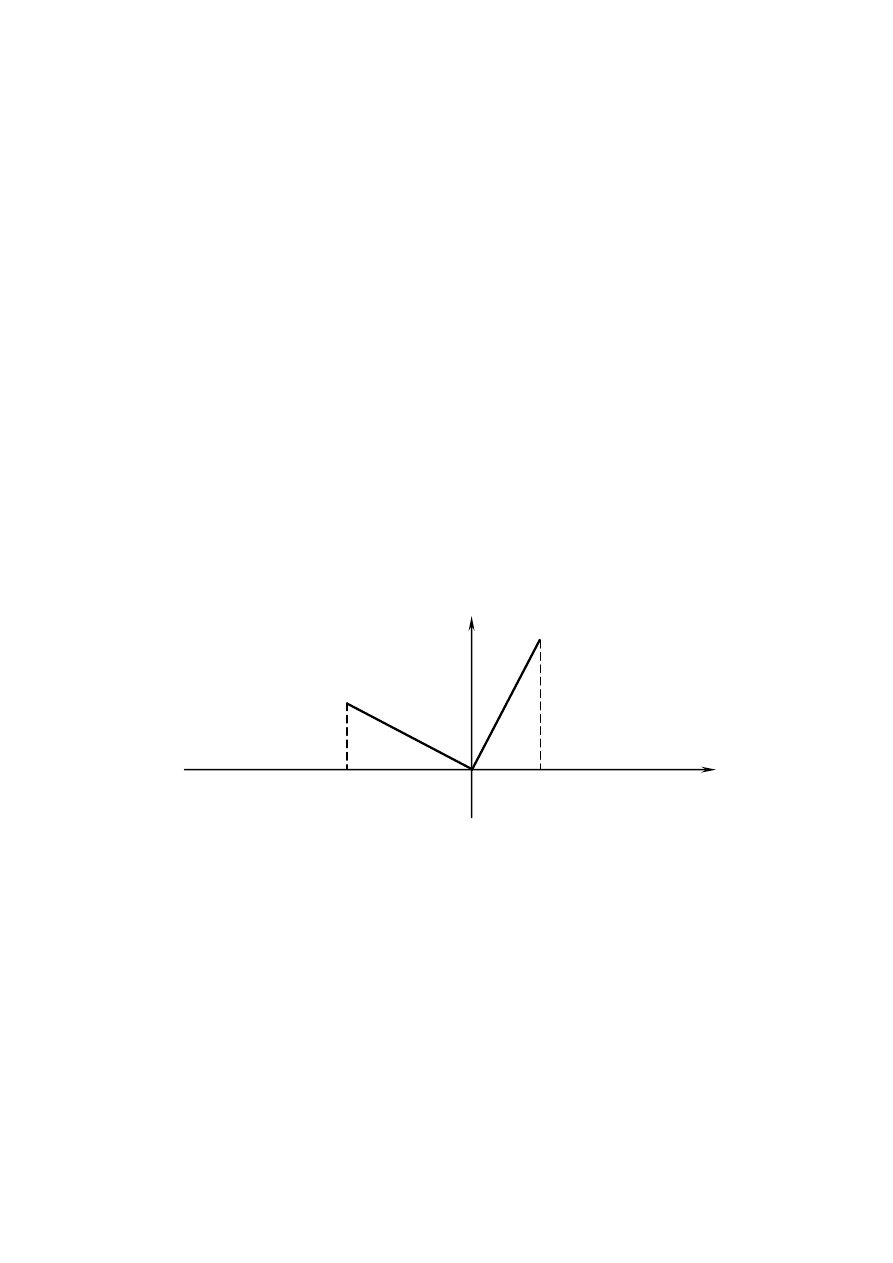
7

Skalowanie polega na pomnożeniu każdego wektora własnego przez skalar skalujący c

i

 

   

 

,

,

2

2

2

1

1

1

a

c

a

a

c

a

sk

sk





(4.36)

przy czym stałe c

1

oraz c

2

oblicza się z równań

{ }

[

]

{ }

{ }

[

]

{ }

.

1

=

,

1

=

2

2

2

2

1

1

2

1

a

M

a

c

a

M

a

c

T

T

(4.37)

Dla układu o dwóch stopniach swobody ortogonalność wektorów własnych można łatwo zilustrować,

co pokazano na rys. 4.3.

Równanie (4.2) w postaci zwartej jest następujące

 

 

 

   

,

0





X

K

X

M





(4.38)

a jego rozwiązanie zależy od warunków początkowych. Dla rozważanego układu o dwóch stopniach

swobody można to wyrazić jako





,

)

0

(

)

0

(

)

0

(

2

1















X

X

X

(4.39)

oraz

 

.

)

0

(

)

0

(

)

0

(

2

1















X

X

X







(4.40)

Rys. 4.3. Ortogonalność wektorów własnych

Różniczkowe równania ruchu drgającego mas są sprzężone (4.1, 4.38). Łatwo można, z uwagi na

wykazaną uprzednio ortogonalność, dokonać operacji ich rozprzężenia, wprowadzając tzw. współrzędne
modalne ξ będące przemieszczeniami, przy czym

 

 

 

.





sk

A

X

(4.41)

Podstawiając zależność (4.41) do (4.38) uzyskuje się

  

 

  

   

.

0









sk

sk

A

K

A

M





(4.42)

Mnożąc lewostronnie uzyskaną zależność przez transponowaną macierz modalną dochodzi się do

równania

    

 

    

   

.

0









sk

T

sk

sk

T

sk

A

K

A

A

M

A





(4.43)

Moda I

Moda II

b

a

a

b

8

Ze względu na ortogonalność obydwa człony równania (4.43) stojące przy współrzędnych modalnych

są macierzami diagonalnymi, co świadczy o rozprzęgnięciu równań ruchu drgającego przez
wprowadzenie nowych współrzędnych ξ, zatem

 

 

 

 

 

 

 

 

 

 

 

 

.

0

,

0

2

2

2

2

2

2

1

1

1

1

1

1

















sk

T

sk

sk

T

sk

sk

T

sk

sk

T

sk

a

K

a

a

M

a

a

K

a

a

M

a









(4.44)

Można te równania również przedstawić inaczej, mianowicie

 

 

 

 

 

 

 

 

 

 

 

 

.

0

,

0

2

2

2

2

2

2

1

1

1

1

1

1

















sk

T

sk

sk

T

sk

sk

T

sk

sk

T

sk

a

M

a

a

K

a

a

M

a

a

K

a









(4.45)

Współczynnik znajdujący się przy współrzędnej modalnej ξ

1

zwany jest współczynnikiem Rayleigha

i równa się kwadratowi naturalnej częstości pierwszej mody. Równania (4.45) uzyskują zatem postać

.

0

,

0

2

2
2

2

1

2

1

1





























(4.46)

Rozwiązaniem równań (4.46) jest

,

sin

cos

,

sin

cos

2

2

2

2

2

1

1

1

1

1

t

D

t

C

t

D

t

C





















(4.47)

przy czym stałe całkowania można obliczyć z warunków początkowych. Jeśli wektory własne zostały

unormowane, zależność (4.34), to mnożąc oczywisty związek





 

 

,

)

0

(

)

0

(





sk

A

X

(4.48)

lewostronnie przez

   

M

A

T

sk

otrzymuje się

    

 

   





)

0

(

)

0

(

X

M

A

A

M

A

T

sk

sk

T

sk





,

(4.49)

co odpowiada

 

 

   





,

)

0

(

)

0

(

X

M

A

E

T

sk





(4.50)

lub

 

   





)

0

(

)

0

(

X

M

A

T

sk





(4.51)

i podobnie

 

   

 

)

0

(

)

0

(

X

M

A

T

sk









.

(4.52)

Ponieważ dane są warunki początkowe (4.39) i (4.40) można wyznaczyć

 

)

0

(



oraz

 

)

0

(





a następnie stałe całkowania. Z kolei, ponieważ znane są wartości składowych wektora

 



, można

znaleźć rzeczywiste przemieszczenia mas z zależności (4.41).

9

Przedstawione rozważania można uogólnić dla układów o n – stopniach swobody, dokonując

stosownych działań macierzowych za pomocą dostępnych bibliotek profesjonalnego oprogramowania
matematycznego.

1.3. Wnioski z rozważań teoretycznych

Z przedstawionej w poprzednim podrozdziale teoretycznej analizy wynika, że masy układu o wielu

stopniach swobody można pobudzić do drgań z pojedynczą częstością naturalną tylko wówczas, gdy
każdej masie nadamy takie wychylenia początkowe, że ich stosunki odpowiadają ilorazom
odpowiadających im wartości składowych wektora modalnego dla danej częstości naturalnej.

Można łatwo stwierdzić, że w przypadku układu dwumasowego o masach m

1

= m

2

= m = 1, ze

sprężynami o jednakowych sztywnościach k

1

= k

2

= k = 1, wartości własne są równe

618034

,

0

0,381966,

2

5

3

1

2

1













o

o

,

oraz

618034

,

1

;

618034

,

2

2

5

3

2

2

2













o

o

.

Macierz modalna ma postać

 

















1

1

618034

,

1

618034

,

0

A

,

natomiast skalowana macierz modalna jest następująca

 

















525773

,

0

850650

,

0

850665

,

0

525730

,

0

sk

A

.

(4.53)

W wyniku obliczeń otrzymuje się

    













































1

0

0

1

00002

,

1

10

78

,

2

10

3

,

7

999997

,

0

6

6

sk

T

sk

A

M

A

,

oraz

    













































618034

,

2

0

0

381965

,

0

618034

,

2

10

78

,

2

10

78

,

2

381965

,

0

6

6

sk

T

sk

A

K

A

.

Rozprzężone równania ruchu, we współrzędnych modalnych, mają zatem postać

 

   

0

618034

,

2

0

0

381965

,

0

1

0

0

1





































.

Rozpatrzone będą teraz dwa różne przypadki wzbudzenia drgań analizowanego układu. Pierwszy

z nich odpowiada następującym początkowym wartościom składowych wektora

 

 





























0

0

)

0

(

,

1

1

)

0

(

x

x



.

10

W wyniku obliczeń otrzymuje się

 

   

 

,

C

C

850665

,

0

52573

,

0

)

0

(

)

0

(

)

0

(

)

0

(

2

1

2

1





















































x

M

A

T

sk

 

















































0

0

D

D

,

)

0

(

)

0

(

)

0

(

2

1

2

1







,

a następnie podstawiając uzyskane wartości do równania (4.48) można obliczyć

 

















































t

t

t

t

A

t

x

t

x

sk

618054

,

1

cos

447221

,

0

618033

,

0

cos

447212

,

0

618054

,

1

cos

728722

,

0

618033

,

0

cos

276392

,

0

)

0

(

)

0

(

)

(

)

(

2

1

2

1

.

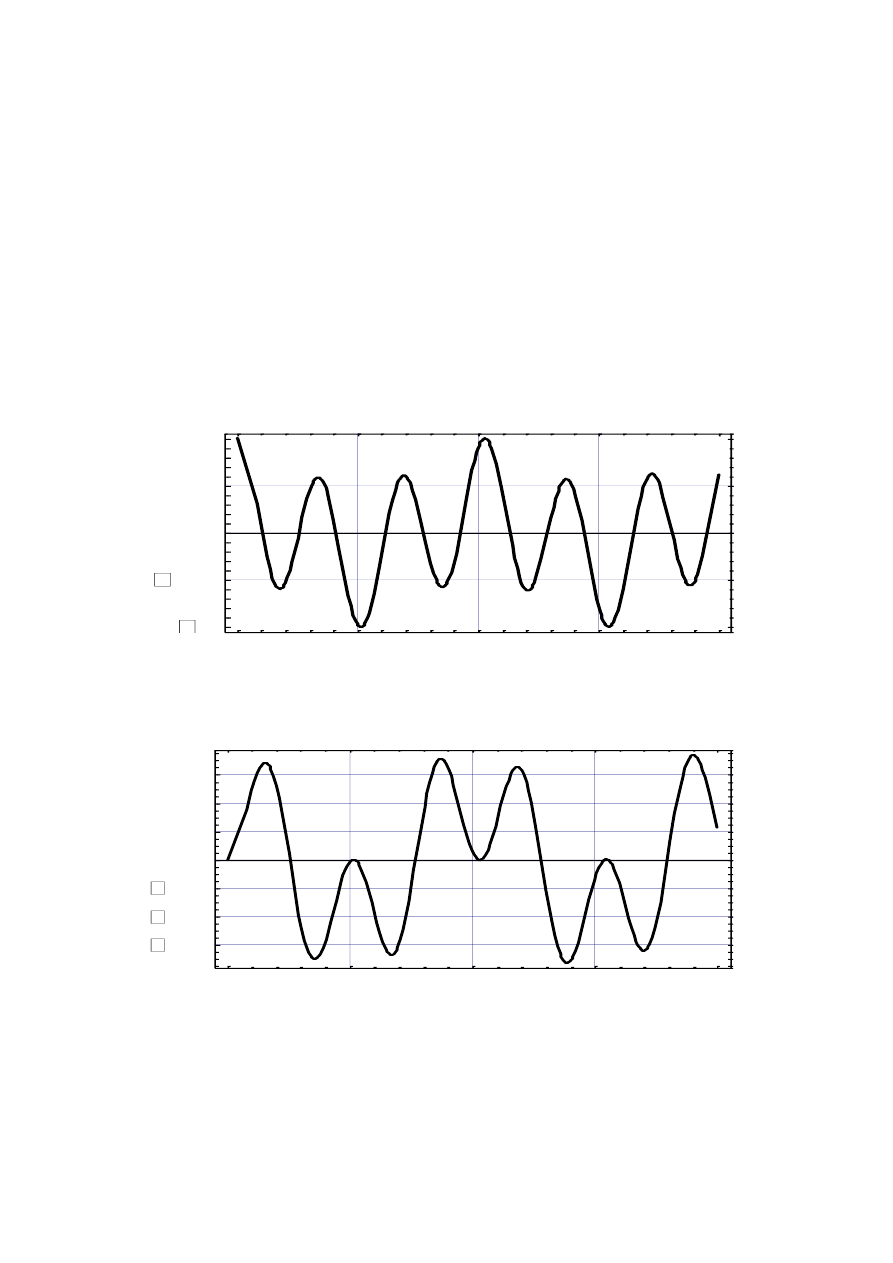
Przebieg czasowy masy pierwszej przedstawiono na rys. 4.4, natomiast drugiej na rys. 4.5.

Rys. 4.4. Przebieg czasowy drgań masy m

1

, dla x

1

(0) = x

2

(0) = 1

Rys. 4.5. Drgania masy m

1

, dla x

1

(0) = x

2

(0) = 1

W drugim przypadku masy układu wychylono z położenia równowagi o wartości równe wartościom

składowych pierwszego wektora modalnego skalowanego, które zgodnie z (4.53) są równe

 

 





























0

0

)

0

(

,

850650

,

0

525730

,

0

)

0

(

x

x



.

0

5

10

15

20

1

0.5

0

0.5

1

t

x

1

0

5

10

15

20

0.6

0.4

0.2

0

0.2

0.4

0.6

t

x

2

11

W wyniku obliczeń otrzymuje się

 

   

 

,

0

381965

,

0

C

C

10

42

,

1

381965

,

0

)

0

(

)

0

(

)

0

(

)

0

(

2

1

6

2

1







































































x

M

A

T

sk

a następnie

[ ]

618033

,

0

cos

324919

,

0

618033

,

0

cos

200810

,

0

=

)

0

(

)

0

(

=

)

(

)

(

2

1

2

1

t

t

ξ

ξ

A

t

x

t

x

sk

.

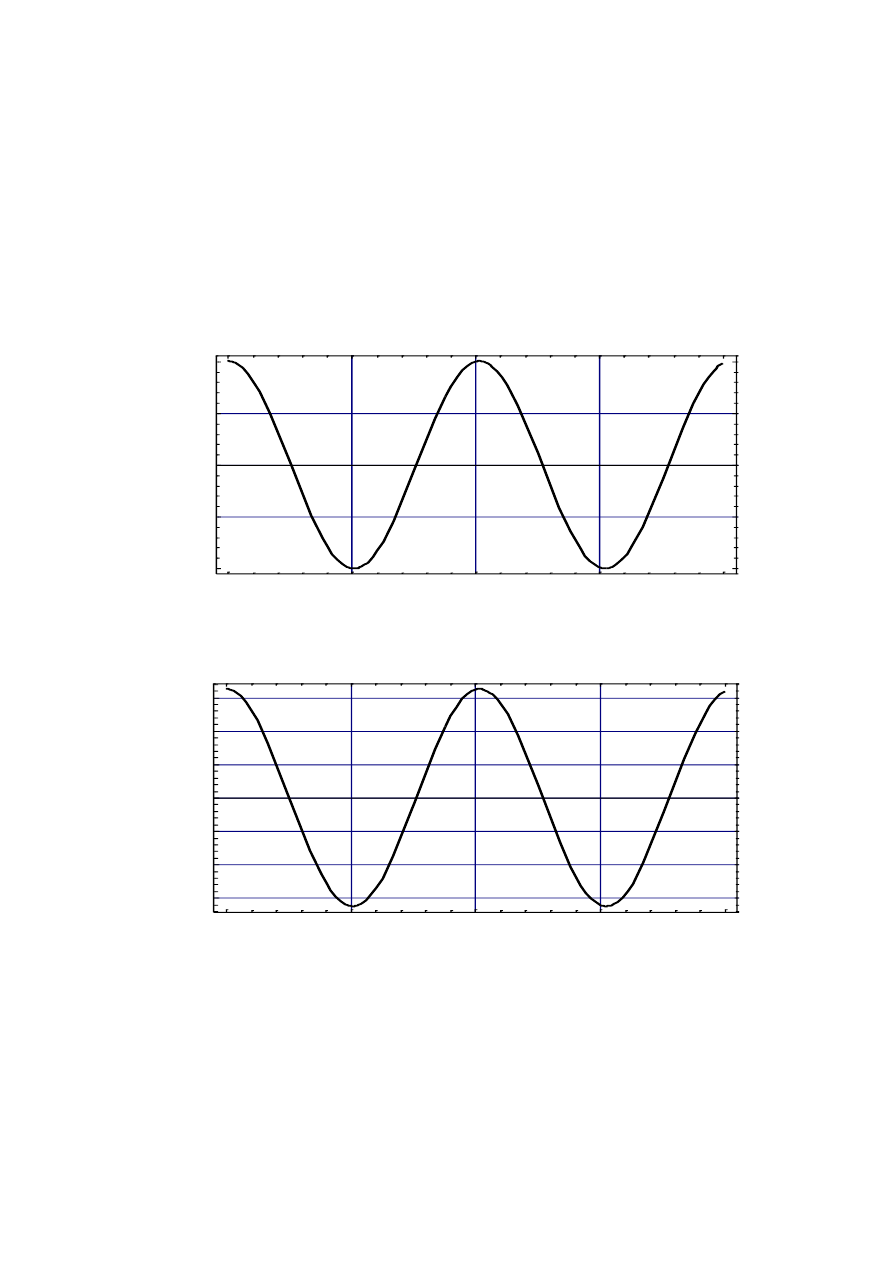
Otrzymane przebiegi czasowe mas przedstawiono odpowiednio na rys. 4.6 i rys. 4.7.

0

5

10

15

20

-

0.2

-

0.1

0

0.1

0.2

t

x

1

Rys. 4.6. Przebieg czasowy drgań masy m

1

, dla pierwszej mody

0

5

10

15

20

-

0.3

-

0.2

-

0.1

0

0.1

0.2

0.3

t

x

1

Rys. 2. Przebieg czasowy drgań masy m

2

, dla pierwszej mody

Przedstawione wyniki obliczeń wskazują wyraźnie, że w czasie wykonywania ćwiczenia należy się

liczyć z możliwością wystąpienia trudności przy wyznaczaniu okresów drgań naturalnych układu, które
będą tym większe, im iloraz początkowych wychyleń obu mas, mierzonych względem położenia
równowagi statycznej układu, będzie bardziej różnić się od ilorazu składowych wektorów modalnych
ujętych w macierzy modalnej wyznaczonej dla rzeczywistych parametrów mechanicznych badanego
układu drgającego.

12

1.4. Przebieg ćwiczenia

Stanowisko pomiarowe stanowi sztywna rama, do której podwieszane są na walcowych sprężynach

dwie masy o konfiguracji odpowiadającej rys. 4.1.

Przed rozpoczęciem właściwych pomiarów dotyczących wyznaczenia częstości naturalnych drgań

układu oraz postaci drgań swobodnych należy dokonać identyfikacji mas i sztywności modelu. W tym
celu wyznacza się kolejno masy poszczególnych obciążników dokonując pomiaru ich cech
geometrycznych, przyjmując, że obciążniki wykonane są ze stali St1, której gęstość

ρ

= 7.86

g/cm

3

.

Zarówno obciążniki jak i sprężyny należy wcześniej ponumerować. Następnie wyznacza się wydłużenia
statyczne pojedynczych sprężyn, zawieszając je kolejno na ramie i obciążając każdym ponumerowanym
obciążnikiem. Należy obliczyć średnią wartość sztywności każdej sprężyny.

Posługując się formułami (4.10) obliczyć należy naturalne częstości drgań własnych badanego układu

a następnie na podstawie zależności (4.14) i (4.15) wyznacza się macierz modalną, której składowymi
należy posłużyć się przy wzbudzaniu kolejno, odpowiednio pierwszej i drugiej mody drgań.

Zgodnie z rys. 4.2 można zauważyć, że pierwsza moda odpowiada drganiom współbieżnym, natomiast

druga drganiom przeciwbieżnym. W związku z tym należy wykonać obserwację drgań własnych
badanego układu, po wzbudzeniu kolejno drgań współ- i przeciwbieżnych w przypadku, gdy warunki
początkowe odpowiadające przemieszczeniom początkowym będą różnić się od obliczonych składowych
macierzy modalnej układu.

Po wzbudzeniu drgań układu odpowiadających kolejno pierwszej i drugiej modzie, należy zmierzyć

czas pełnych dwudziestu okresów drgań.

1.5. Zawartość sprawozdania

Sprawozdanie z przebiegu ćwiczenia winno zawierać:

 opis celu i zakresu badań,
 schemat stanowiska pomiarowego,
 wyniki pomiarów geometrycznych cech obciążników,
 wyniki pomiarów geometrycznych obciążonych i nieobciążonych sprężyn,
 obliczenia mas obciążników i współczynników sztywności sprężyn,
 podstawowe, niezbędne formuły zastosowane, w przyjętej konfiguracji ponumerowanych

obciążników i sprężyn, do obliczenia częstości naturalnych układu i macierzy modalnej,

 wyniki obliczeń wykonanych na podstawie zastosowanych formuł,



wyniki obliczeń okresu, częstotliwości i kołowej częstości naturalnych drgań

ω

o1

i

ω

o2

układu,



poglądowy rysunek postaci drgań własnych dyskretnych mas stanowiska pomiarowego użytego
w ćwiczeniu, wraz z opisem liczbowym wartości

a

ij

, podobnie jak to pokazano na rys. 4.2,



opis błędów pomiarów,



sformułowane wnioski dotyczące uzyskanych wyników, przebiegu ćwiczenia i znaczenia analizy
modalnej w praktyce inżynierskiej, w zakresie podstaw teoretycznych zamieszczonych w instrukcji
ćwiczenia.

1.6. Literatura

[1] Ewins D. J.: Modal Testing: Theory and Practice. Research Studies Press Ltd Taunton, Somerset,

England, John Willey & Sons Inc., New York 1995 (revised with new notation).

[2] Irvine H. M.: Structural Dynamics for the Practising Engineer. Allen & Unwin, London 1986.

[3] Uhl T.: Komputerowo wspomagana identyfikacja modeli konstrukcji mechanicznych. Wspomaganie

komputerowe CAD/CAM. WN-T, Warszawa 1997.

[4] Wojnarowski J.: Metodyczne ćwiczenia laboratoryjne z mechanicznej teorii maszyn. Skrypt

Uczelniany Pol. Śląskiej, nr 1162, wyd. IV, Gliwice 1993.