© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

TERMODYNAMIKA

PROCESOWA I TECHNICZNA

Wykład X

Wyznaczanie wielkości cząstkowych

Równania stanu dla roztworów

Fugatywność w roztworach

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

2

Komunikat

Egzamin z „Termodynamiki procesowej i technicznej”

w semestrze zimowym 2013/14 odbędzie się

w terminach:

PN 27.01.2014 10.15 – 12.15 s. B-1 F-4 termin „0”

PT 7.02.2014

8.00 – 10.00 s. 310 A-2 I termin

PN 17.02.2014 9.00 – 11.00 s. B-1 F-4 II termin

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY –

Wielkości cząstkowe cd.

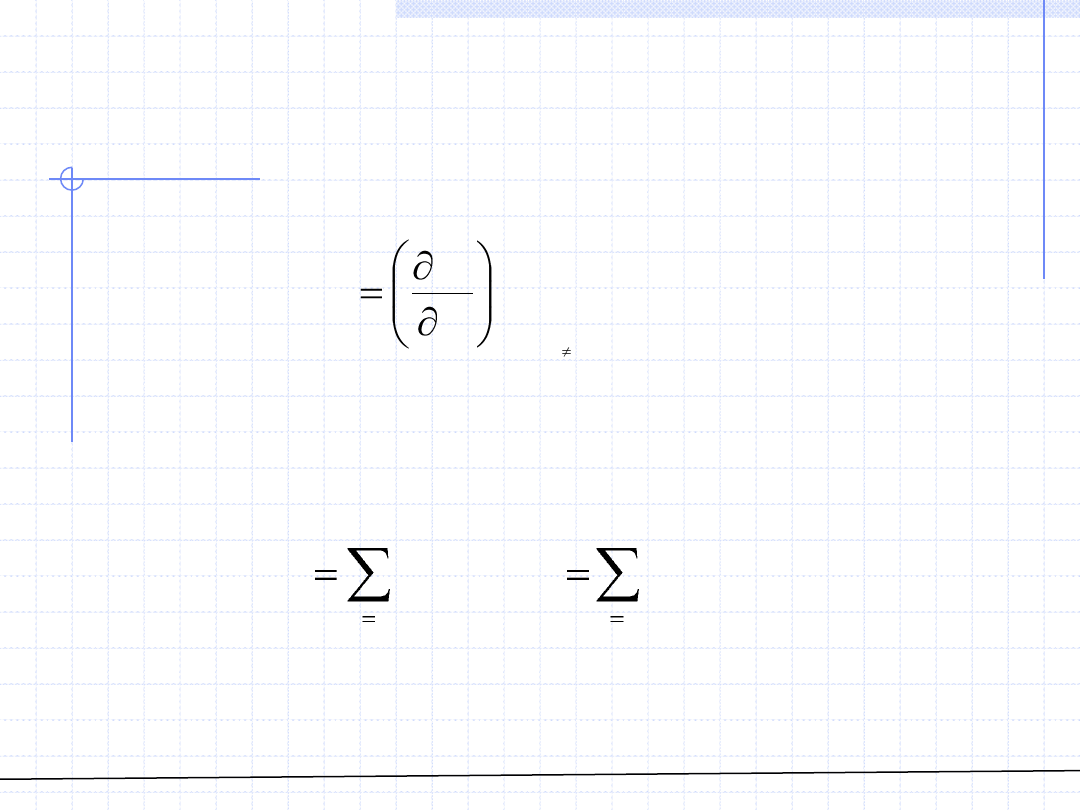
Przypomnijmy wzór definicyjny określający wielkości cząstkowe:

i

j

n

p

T

i

i

n

W

w

,

,

Znajomość wielkości cząstkowych i składu roztworu pozwala na obliczenie

danej wielkości ekstensywnej:

k

i

i

i

k

i

i

i

w

x

w

w

n

W

1

1

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY –

Wielkości cząstkowe cd.

Wielkości cząstkowe zależą od ciśnienia i temperatury a także od składu

danego roztworu. Są również ściśle związane z wielkościami właściwymi

czystych składników. Dla ustalonego ciśnienia i temperatury można napisać:

)

,...,

,...,

,

,

(

2

1

0

k

i

i

i

x

x

x

x

w

f

w

Funkcja powyższa musi spełniać własności graniczne:

i

i

x

i

i

x

w

w

w

w

i

i

)

(

)

(

lim

lim

0

0

1

Wartość „w

i

∞

” oznacza tzw. wielkość cząstkową w roztworze nieskończenie

rozcieńczonym.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY –

Wyznaczanie wielkości cząstkowych

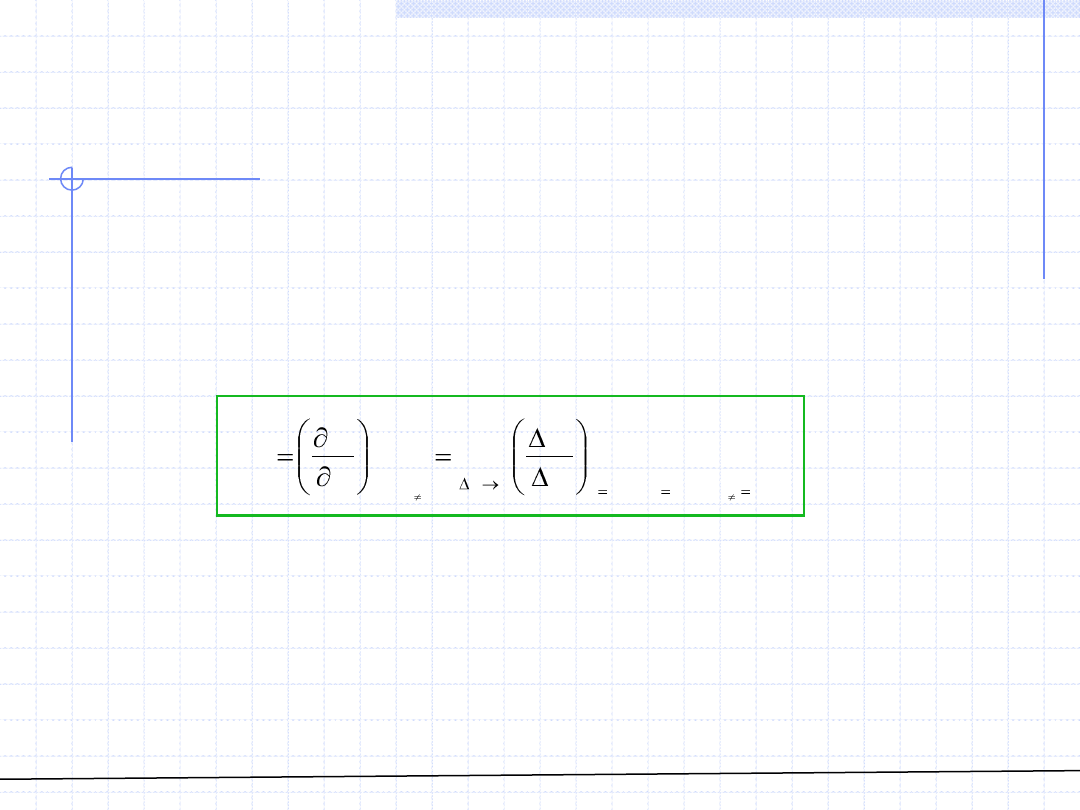
W przypadku gdy daną wielkość W można wyznaczyć eksperymentalnie, istnieje

możliwość określenia wielkości cząstkowych bezpośrednio za pomocą doświadczeń

oraz wzoru definicyjnego:

.

.,

.,

0

,

,

lim

const

n

const

p

const

T

i

n

n

p

T

i

i

i

j

i

i

j

n

W

n

W

w

gdzie ΔW oznacza zmierzony eksperymentalnie przyrost wartości W po dodaniu

do roztworu składnika „i” w ilości Δn

i

.

Metodę tę można stosować np. do wyznaczania objętości cząstkowych.

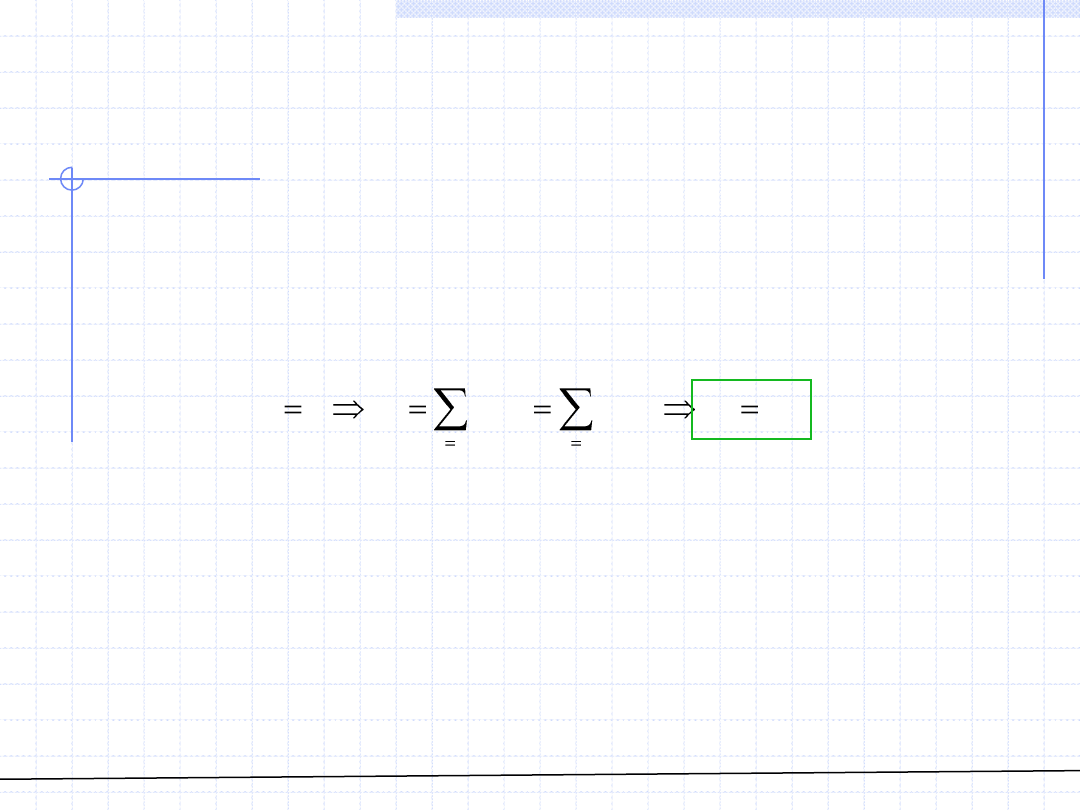
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY –

Wyznaczanie wielkości cząstkowych

W szczególnych sytuacjach gdy dana wielkość mieszania jest równa 0, wielkości

cząstkowe są równe wielkościom właściwym czystych składników i nie zależą

od składu roztworu:

0

0

1

1

0

k

k

M

i

i

i

i

i

i

i

i

W

W

n w

n w

w

w

Sytuacja taka ma miejsce w przypadku objętości, entalpii i energii wewnętrznej

roztworów idealnych.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY –

Wyznaczanie wielkości cząstkowych

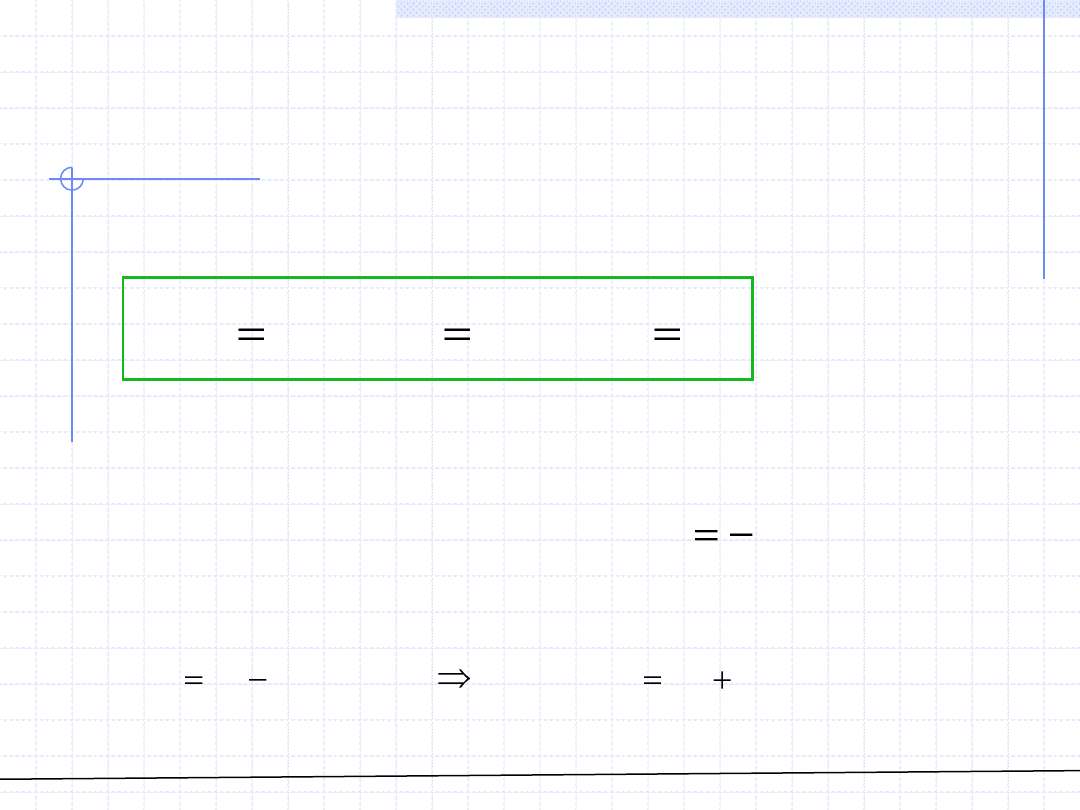
Dla roztworów idealnych wyznaczanie wielkości cząstkowych jest stosunkowo

proste. Mamy bowiem:

0

0

0

RI

RI

RI

i

i

i

i

i

i

v

v

h

h

u

u

W przypadku entropii, energii swobodnej i entalpii swobodnej należy

skorzystać ze wzorów określających entropię mieszania roztworów idealnych

podanych na poprzednim wykładzie:

,

ln( )

M RI

i

i

i

s

x R

x

Znajomość cząstkowej wielkości mieszania oraz wielkości właściwej czystego

składnika pozwala na obliczenie danej wielkości cząstkowej:

0

i

i

M

i

w

w

w

0

M

i

i

i

w

w

w

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY –

Wyznaczanie wielkości cząstkowych

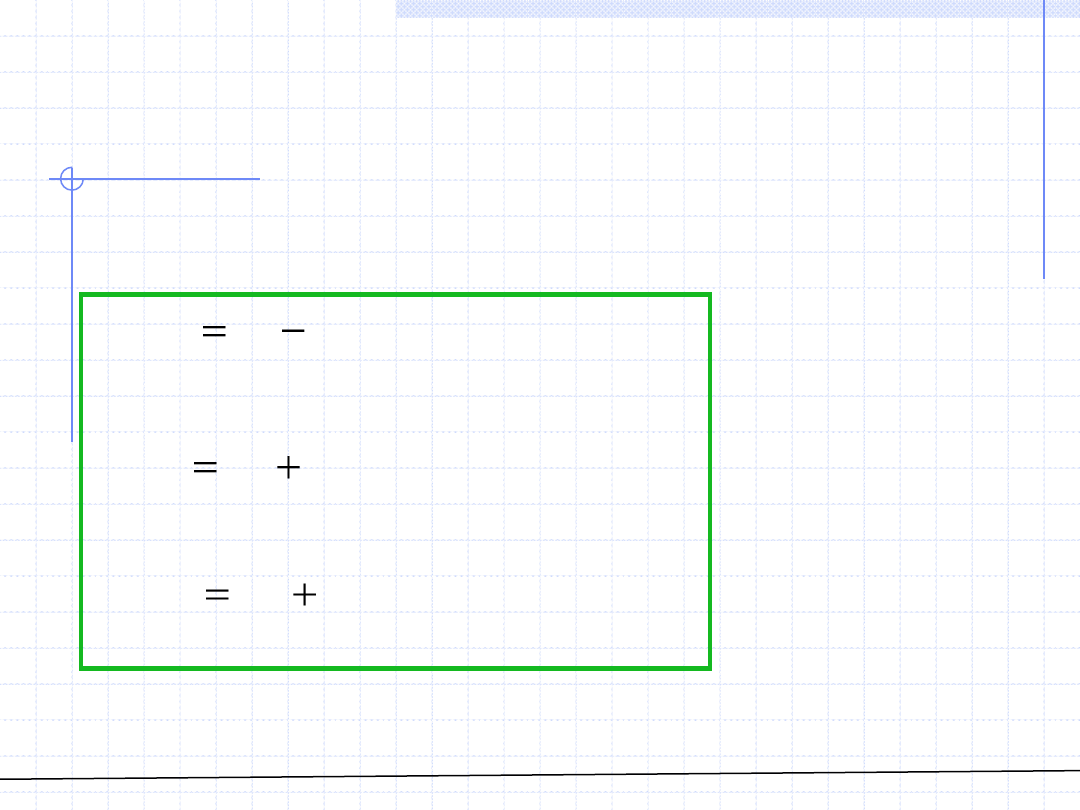
Mamy zatem wzory określające kolejne wielkości cząstkowe dla

roztworów idealnych:

0

ln( )

RI

i

i

i

i

s

s

x R

x

0

ln( )

RI

i

i

i

i

a

a

x RT

x

0

ln( )

RI

i

i

i

i

g

g

x RT

x

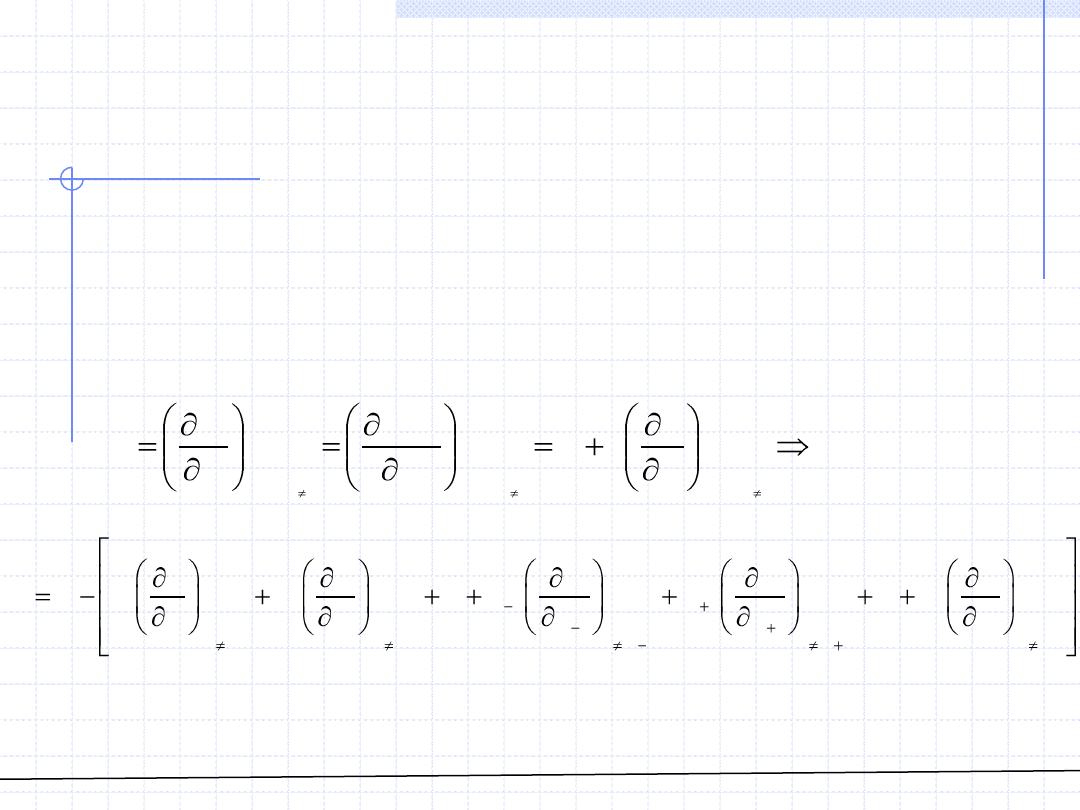
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY –

Wyznaczanie wielkości cząstkowych cd.

W przypadku roztworów rzeczywistych często wyznaczanie wielkości cząstkowych

za pomocą wzoru definicyjnego jest trudne. Można natomiast na ogół bez problemu

wyznaczać wielkości właściwe roztworu jako funkcje składu. Okazuje się, że

na podstawie znajomości wielkości właściwych roztworu można obliczyć wszystkie

wielkości cząstkowe. Wychodząc ze wzoru definicyjnego i stosując zasady

rachunku różniczkowego można otrzymać:

i

j

i

j

i

j

n

p

T

i

n

p

T

i

n

p

T

i

i

n

w

n

w

n

nw

n

W

w

,

,

,

,

,

,

)

(

1

2

1

1

, ,

, ,

, ,

, ,

, ,

1

2

1

1

,1

,2

, 1

, 1

,

...

...

j

j

j

j

j

i

i

i

k

p T x

p T x

p T x

p T x

p T x

i

i

k

j i

j i

j i i

j i i

j i k

w

w

w

w

w

w

w

x

x

x

x

x

x

x

x

x

x

Otrzymany wzór można zapisać w zwartej postaci:

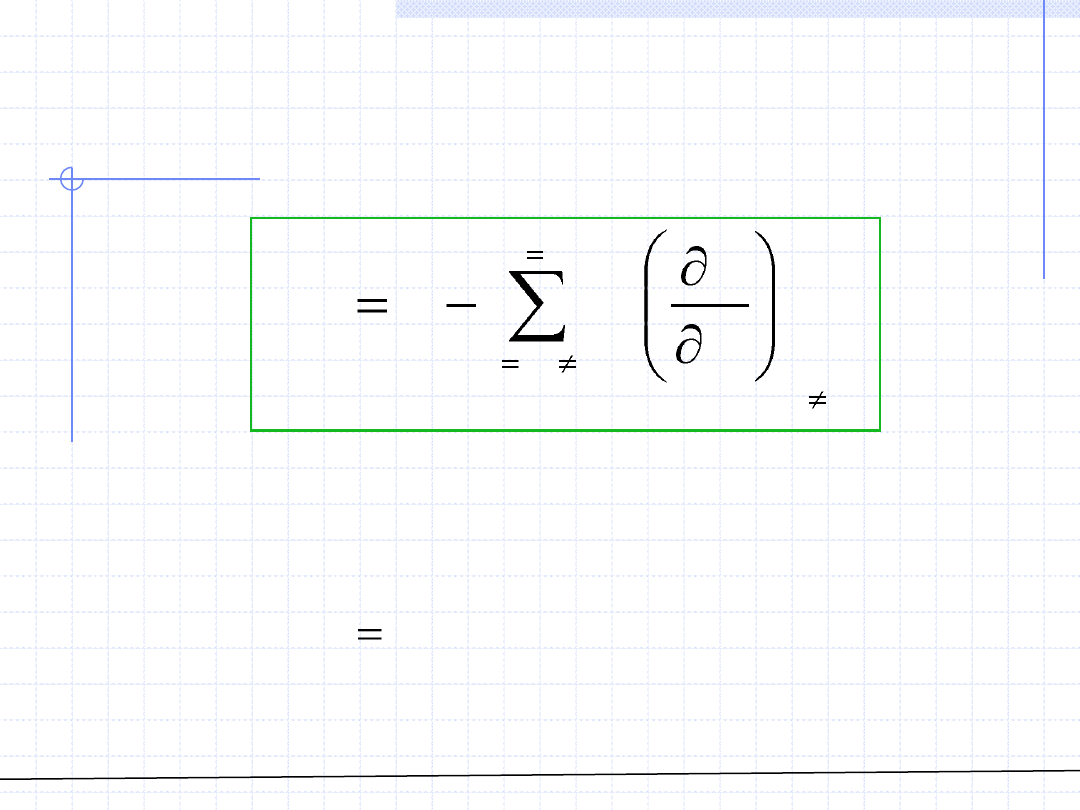
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY –

Wyznaczanie wielkości cząstkowych cd.

)

,...,

,...,

,

(

2

1

k

i

x

x

x

x

f

w

Aby skorzystać z powyższego wzoru należy dysponować zależnością wielkości

właściwej „w” od składu roztworu wyrażonego za pomocą ułamków molowych:

k

r

i

r

r

r

i

j

x

T

p

r

r

i

j

x

w

x

w

w

,

1

,

,

,

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY –

Wyznaczanie wielkości cząstkowych dla

roztworów 2 - składnikowych

)

(

'

)

1

(

)

(

)

1

(

1

1

1

1

1

1

2

2

,

2

2

1

x

w

x

x

w

dx

dw

x

w

dx

dw

x

w

x

w

x

w

w

i

T

p

)

(

'

)

(

2

1

1

1

1

1

1

1

,

1

1

2

x

w

x

x

w

dx

dw

x

w

dx

dw

x

w

x

w

x

w

w

i

T

p

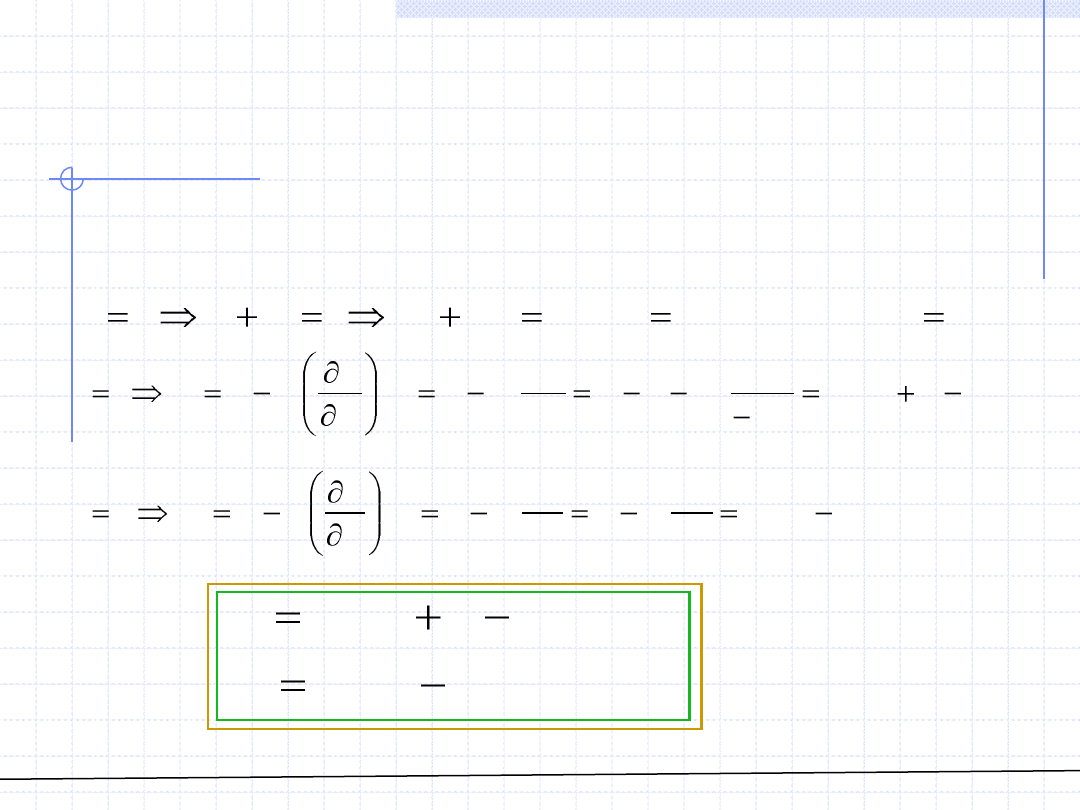
Otrzymany wzór znajduje często zastosowanie w przypadku roztworów

2 – składnikowych (binarnych), dla których k=2, i=1,2

'

/

)

(

0

1

2

1

1

2

1

2

1

w

dx

dw

x

f

w

dx

dx

x

x

k

)

(

'

)

(

)

(

'

)

1

(

)

(

1

1

1

2

1

1

1

1

x

w

x

x

w

w

x

w

x

x

w

w

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY –

Wyznaczanie wielkości cząstkowych dla

roztworów 2 - składnikowych

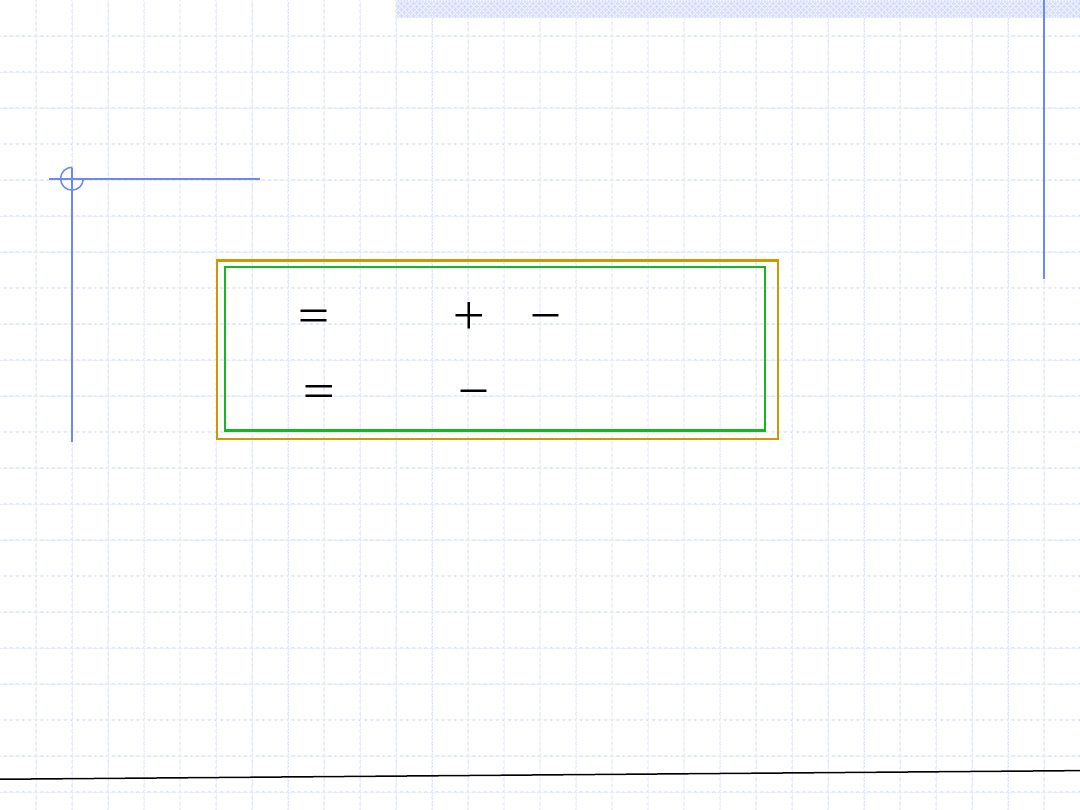
Zastosowanie powyższych wzorów wymaga znajomości funkcji danej wielkości

właściwej w zależności od składu w tym przypadku wyrażonego za pomocą

ułamka molowego składnika 1.

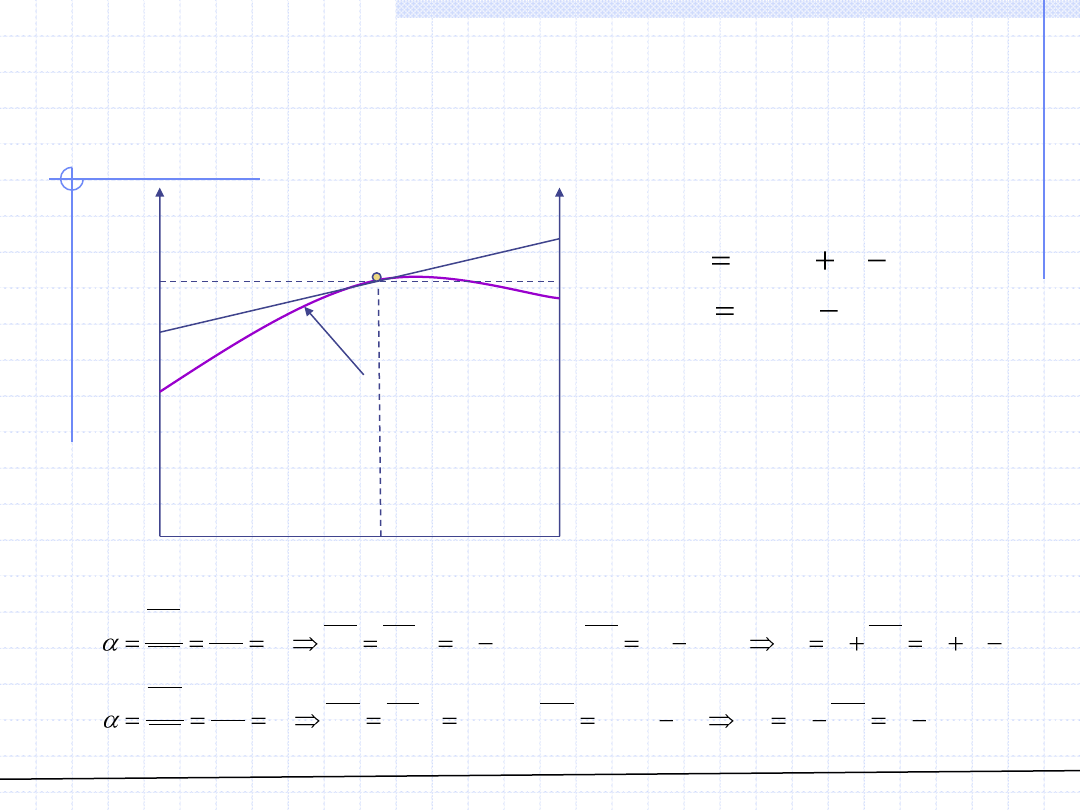
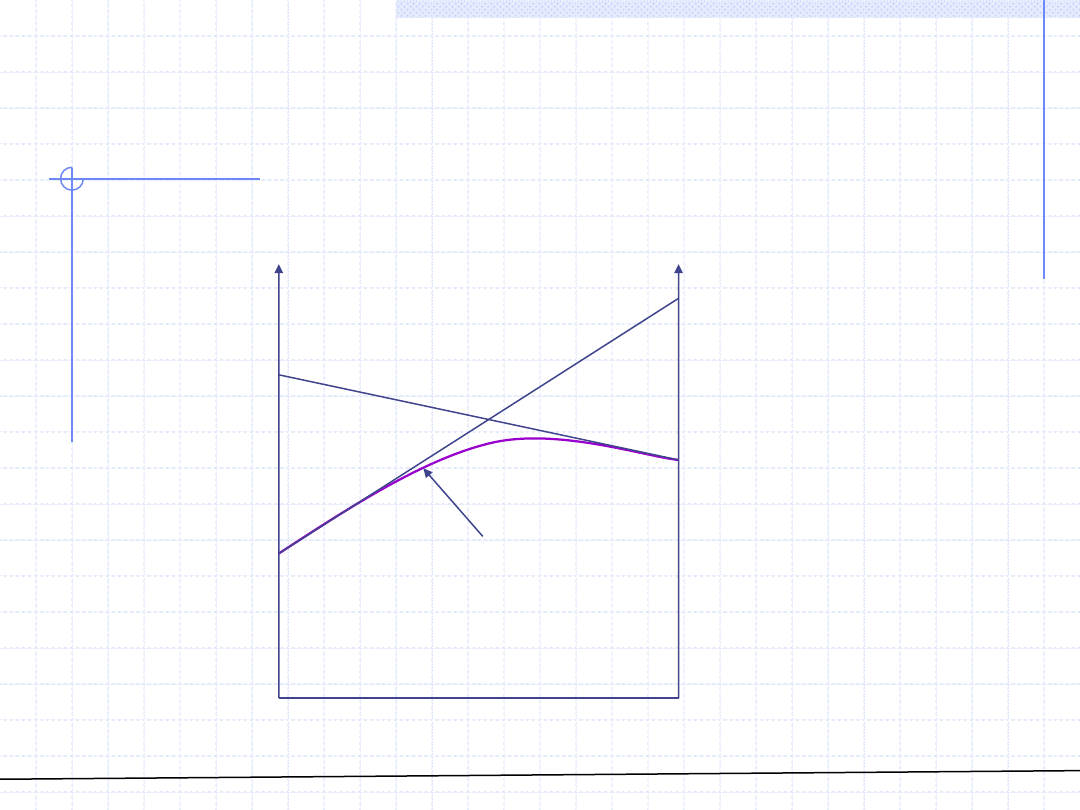
W przypadku gdy zależność ta jest podana w postaci graficznej istnieje

możliwość graficznego wyznaczenia wielkości cząstkowych.

)

(

'

)

(

)

(

'

)

1

(

)

(

1

1

1

2

1

1

1

1

x

w

x

x

w

w

x

w

x

x

w

w

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY –

Wyznaczanie wielkości cząstkowych dla

roztworów 2 – składnikowych cd.

'

)

1

(

)

(

'

)

1

(

'

'

tan

1

1

1

1

1

1

w

x

w

BC

w

w

x

w

w

BC

w

x

w

AB

BC

w

dx

dw

AB

BC

'

)

(

'

'

'

tan

1

2

2

1

1

1

w

x

w

DE

w

w

w

x

w

DE

w

x

w

DA

DE

w

dx

dw

DA

DE

x

1

=0

x

2

=1

x

2

=0

x

1

=1

x

1

->

w(x

1

)

w

w

1

0

w

1

w

2

0

w

2

A

B

C

D

E

w(x

1

)

α

)

(

'

)

(

)

(

'

)

1

(

)

(

1

1

1

2

1

1

1

1

x

w

x

x

w

w

x

w

x

x

w

w

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY –

Wyznaczanie wielkości cząstkowych dla

roztworów 2 – składnikowych cd.

x

1

=0

x

2

=1

x

2

=0

x

1

=1

x

1

->

w(x

1

)

w

1

0

w

1

∞

w

2

0

w

2

∞

Metodą wykreślną można również wyznaczyć wielkości cząstkowe w roztworach

nieskończenie rozcieńczonych w

1

∞

i w

2

∞

.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY – Równania stanu

0

)

,...,

,

,

,

,

(

2

1

k

n

n

n

V

T

p

F

Zależności między najważniejszymi parametrami układu będącego roztworem

opisuje równanie stanu roztworu, którego ogólna postać jest następująca:

Dla układów zamkniętych o ustalonym składzie wygodnie jest stosować

postać, w której występują objętość właściwa i ułamki molowe:

0

)

,...,

,

,

,

,

(

2

1

k

x

x

x

v

T

p

F

Jeżeli chodzi o konkretne postacie równań stanu dla roztworów, to na ogół

stosuje się takie same równania jak dla składników czystych. Podstawowym

problemem są tutaj metody wyznaczania parametrów. Parametry te najczęściej

wyznacza się na podstawie parametrów czystych składników za pomocą tzw.

reguł mieszania.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY – Równania stanu cd.

1

2

(

...

... )

i

k

pV

n

n

n

n RT

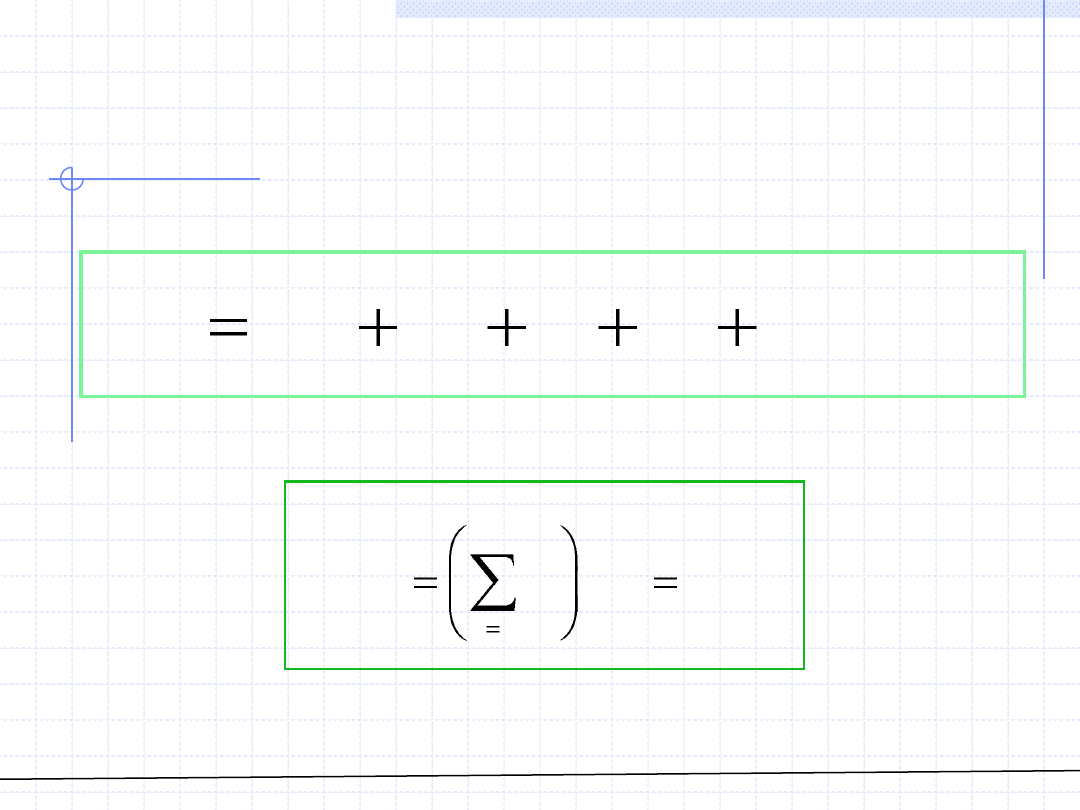
Dla roztworu gazów doskonałych oczywiście obowiązuje RSGD:

1

k

i

i

pV

n RT

nRT

Równanie to można zapisać w zwartej postaci:

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY – Równania stanu cd.

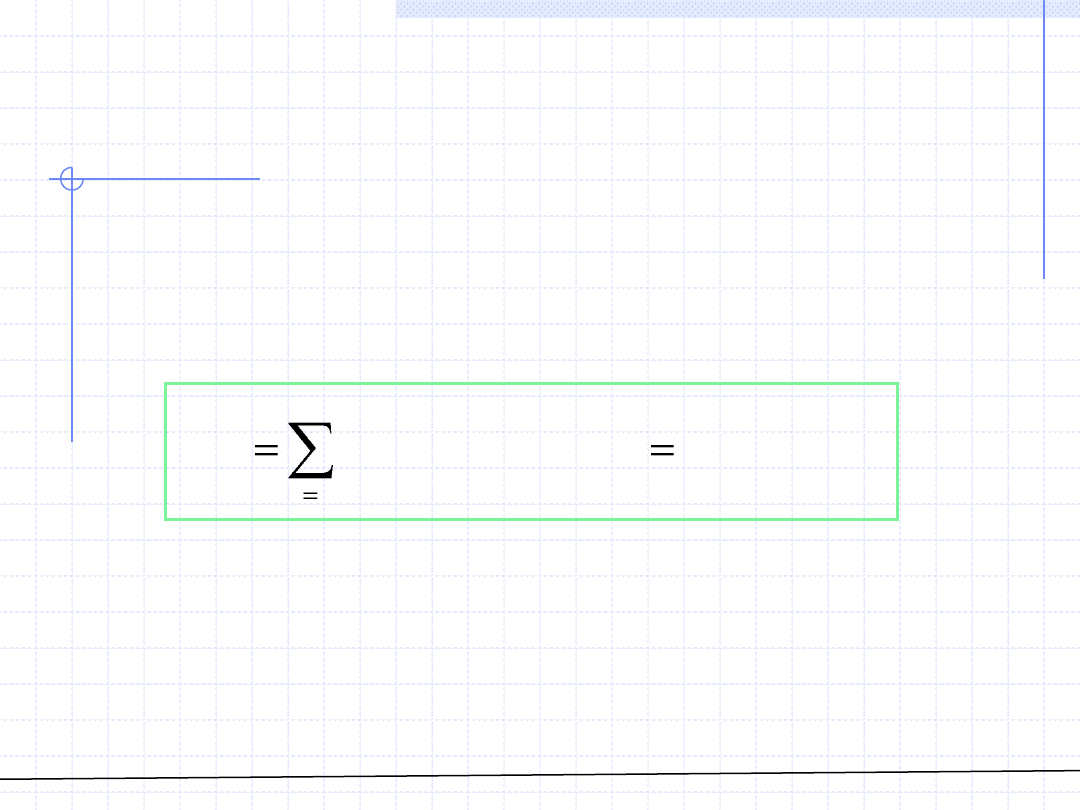
Dla roztworów spełniających prawo Amagata można w zasadzie zastosować

dowolne równanie stanu czystych składników, pod warunkiem, że równanie

to będzie rozwiązane względem objętości:

)

,

,

(

1

0

0

0

T

p

n

f

V

gdzie

V

V

i

k

i

i

i

i

Przykładem takiego postępowania może być zastosowanie równania

wirialnego obciętego po drugim wyrazie:

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY – Równania stanu cd.

)

(

0

1

0

0

T

B

n

p

RT

n

V

gdzie

V

V

i

i

i

k

i

i

i

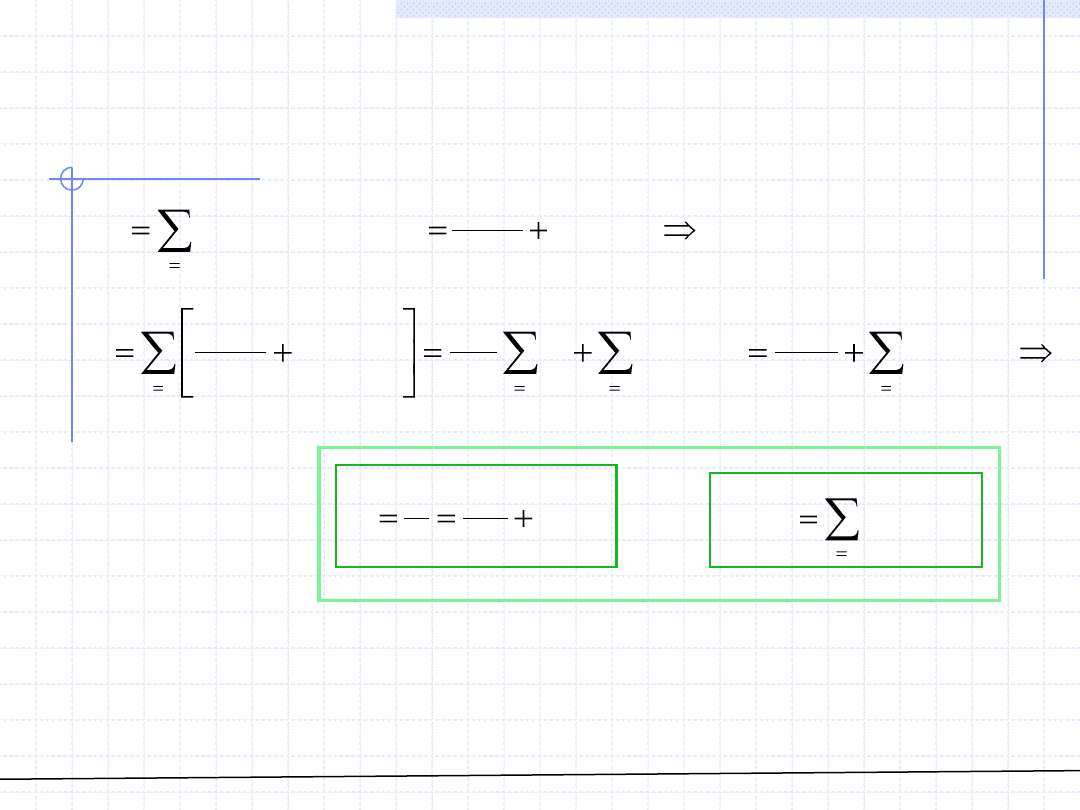
Wzór określający drugi współczynnik wirialu B(T) dla roztworu jest właśnie

przykładem prostej reguły mieszania. Niestety to proste rozwiązanie

ma dosyć ograniczone zastosowanie do obszarów w których można

stosować obcięte równania wirialne z dodatkowym założeniem stosowalności

prawa Amagata.

)

(

)

(

)

(

0

1

1

0

1

1

0

T

B

n

p

nRT

T

B

n

n

p

RT

T

B

n

p

RT

n

V

i

k

i

i

k

i

i

k

i

i

i

k

i

i

i

i

)

(T

B

p

RT

n

V

v

k

i

i

i

T

B

x

T

B

gdzie

1

0

)

(

)

(

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

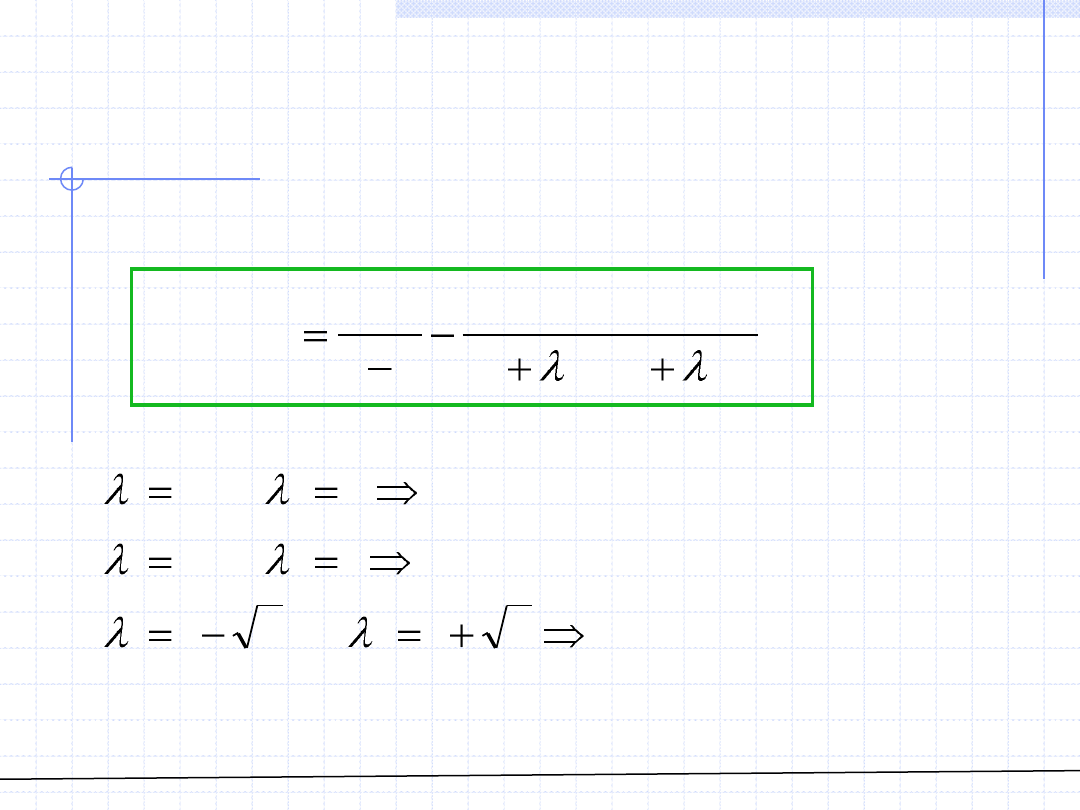
ROZTWORY – Równania stanu cd.

)

)(

(

)

(

)

,

(

2

1

b

v

b

v

T

a

b

v

RT

T

v

p

Równania 3 – go stopnia wywodzące się z równania van der Waalsa można

zapisać w ogólnej postaci:

gdzie λ

1

i λ

2

są to stałe bezwymiarowe liczby charakteryzujące dane równanie.

PR

równanie

SRK

i

RK

równanie

Waalsa

der

van

równanie

2

1

2

1

1

0

0

0

2

1

2

1

2

1

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY – Równania stanu cd.

)

,...,

,

,

,...,

,

(

)

,...,

,

,

,...,

,

(

)

(

2

1

0

0

2

0

1

2

1

0

0

2

0

1

k

k

k

k

x

x

x

b

b

b

f

b

x

x

x

a

a

a

f

T

a

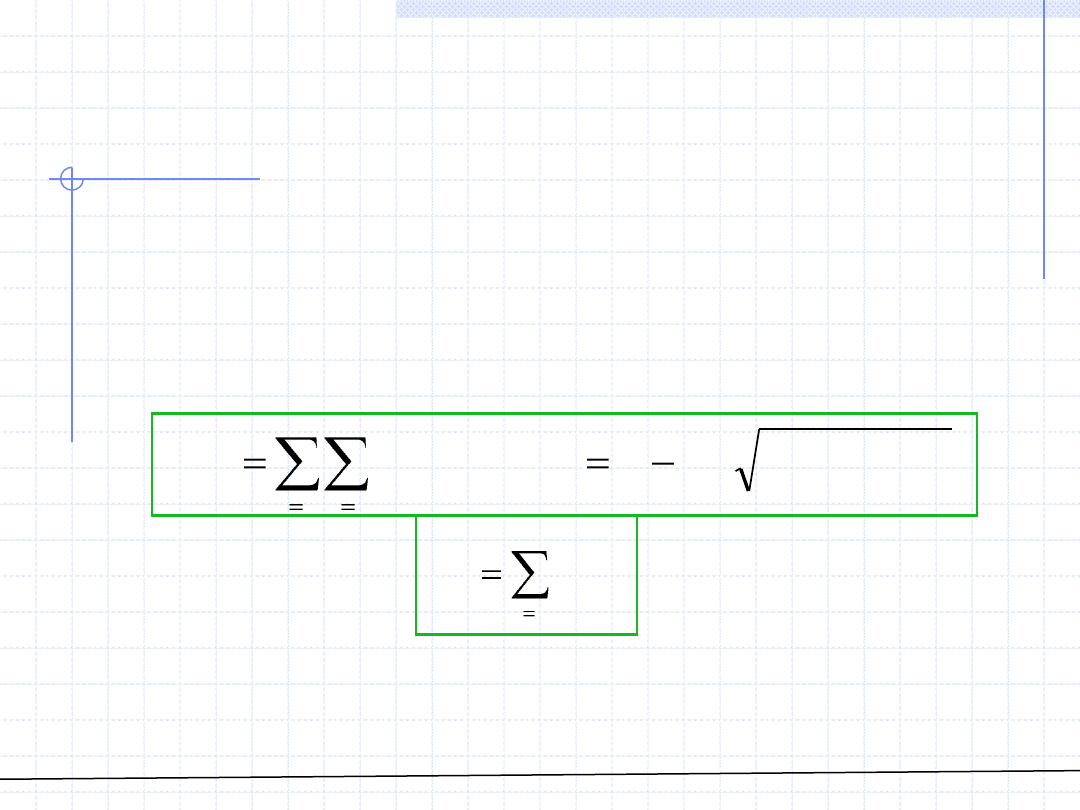
W przypadku roztworów kluczowym problemem jest określenie parametrów

a(T) i b. W ogólnej sytuacji parametry te zależą od odpowiednich parametrów

czystych substancji i składu roztworu:

Konkretne postacie tych zależności nazywamy regułami mieszania.

Zależności te powinny spełniać warunki graniczne:

0

0

1

1

lim

lim

i

i

i

i

i

i

x

x

a x

a

b x

b

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

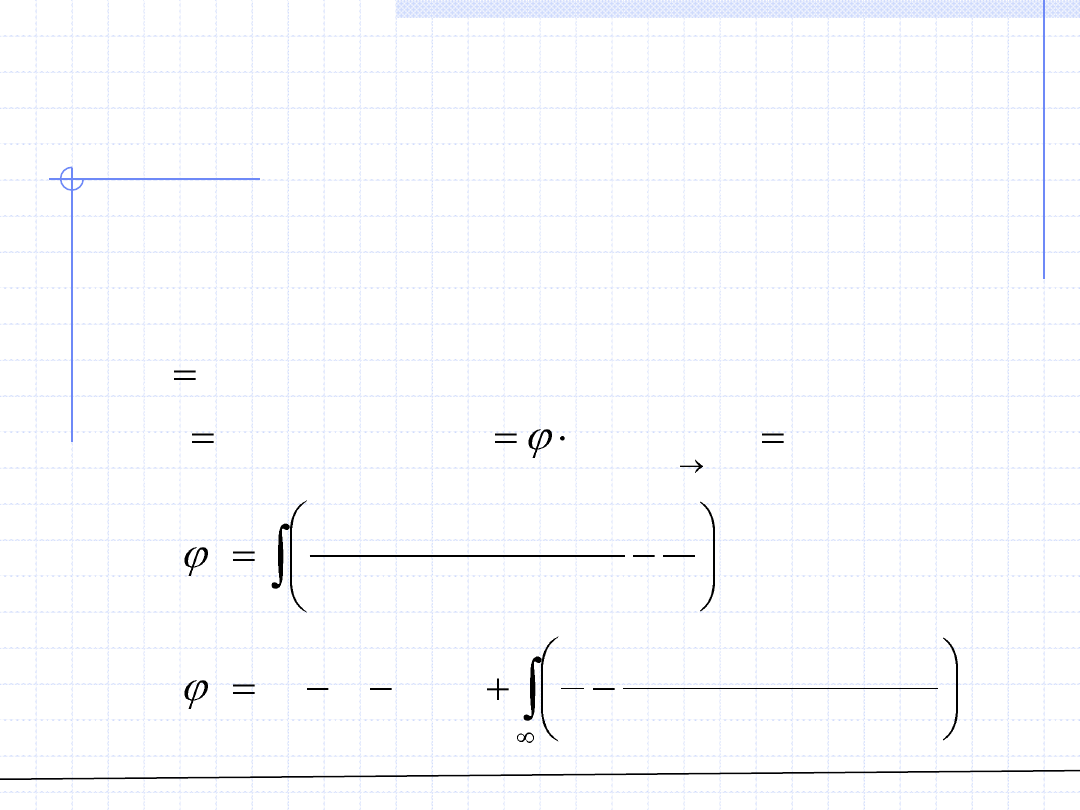
ROZTWORY – Równania stanu cd.

Najczęściej w przypadku równań 3 – go stopnia stosowane są tzw.

kwadratowe reguły mieszania nazywane też regułami van der Waalsa:

k

i

k

j

j

i

ij

ij

ij

j

i

T

a

T

a

k

a

a

x

x

T

a

1

1

0

0

)

(

)

(

)

1

(

)

(

k

i

i

i

b

x

b

1

0

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY – Fugatywność roztworu

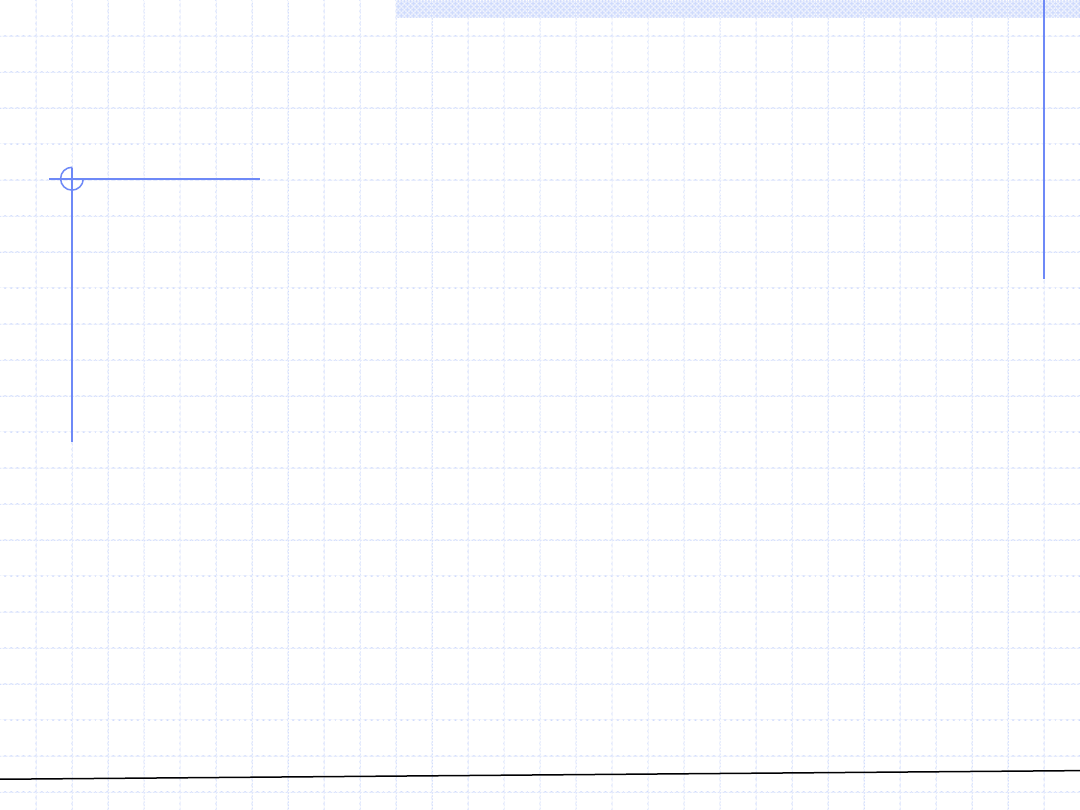
Pojęcie fugatywności odnosi się również do roztworów, gdzie definiuje się

dwie wielkości określane nazwą „fugatywność”. Pierwsza wielkość to

fugatywność całego roztworu, którą będziemy oznaczać jako „f”. Definicja

tej fugatywności jest analogiczna jak dla czystych substancji:

v

k

p

k

p

RT

x

x

x

T

v

p

v

z

z

dp

p

RT

x

x

x

T

p

v

p

f

p

f

f

RTd

dg

const

T

)

,...,

,

,

,

(

1

)

ln(

)

1

(

)

ln(

1

)

,...,

,

,

,

(

)

ln(

lim

)

ln(

.

2

1

0

2

1

0

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY – Fugatywność

składnika w roztworze

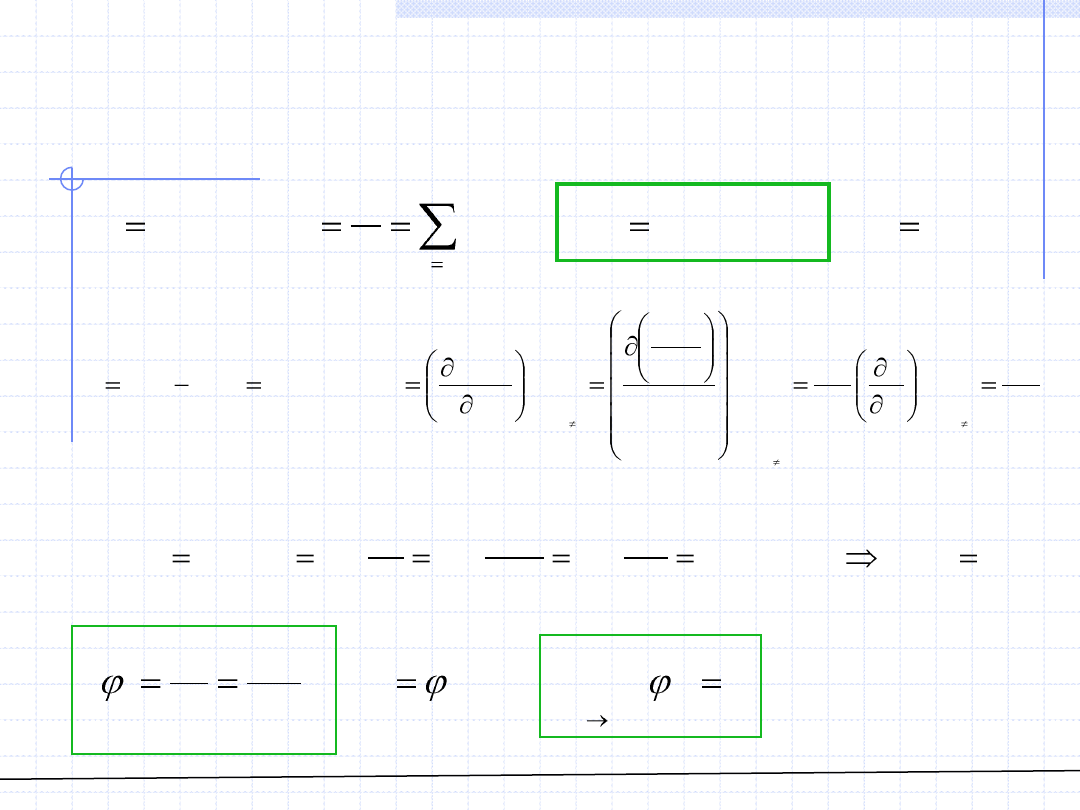
Znacznie ważniejszym pojęciem jest fugatywność składnika w

roztworze.

Wielkość ta odgrywa kluczową rolę w rozważaniach dotyczących

równowag fazowych. Definicja tej wielkości jest analogiczna do definicji

fugatywności roztworu, z tym że tutaj podstawą jest cząstkowa entalpia

swobodna składnika „i”.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY – Fugatywność

składnika w roztworze

.

)

ln(

.

1

const

x

f

RTd

dg

g

x

n

G

g

const

T

i

i

i

k

i

i

i

p

RT

n

n

p

RT

n

p

nRT

n

V

v

dp

v

dT

s

dp

v

dg

i

j

i

j

i

j

n

T

p

i

n

T

p

i

n

T

p

i

GD

GD

i

i

i

i

i

,

,

,

,

,

,

)

(

)

(

i

GD

i

i

i

i

i

i

GD

i

GD

i

p

f

p

RTd

p

dp

RT

py

dpy

RT

p

dp

RT

dp

v

dg

)

(

)

(

)

(

)

ln(

1

)

(

lim

0

i

p

i

i

i

i

i

i

i

i

p

x

f

p

x

f

p

f

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY – Fugatywność

składnika w roztworze cd.

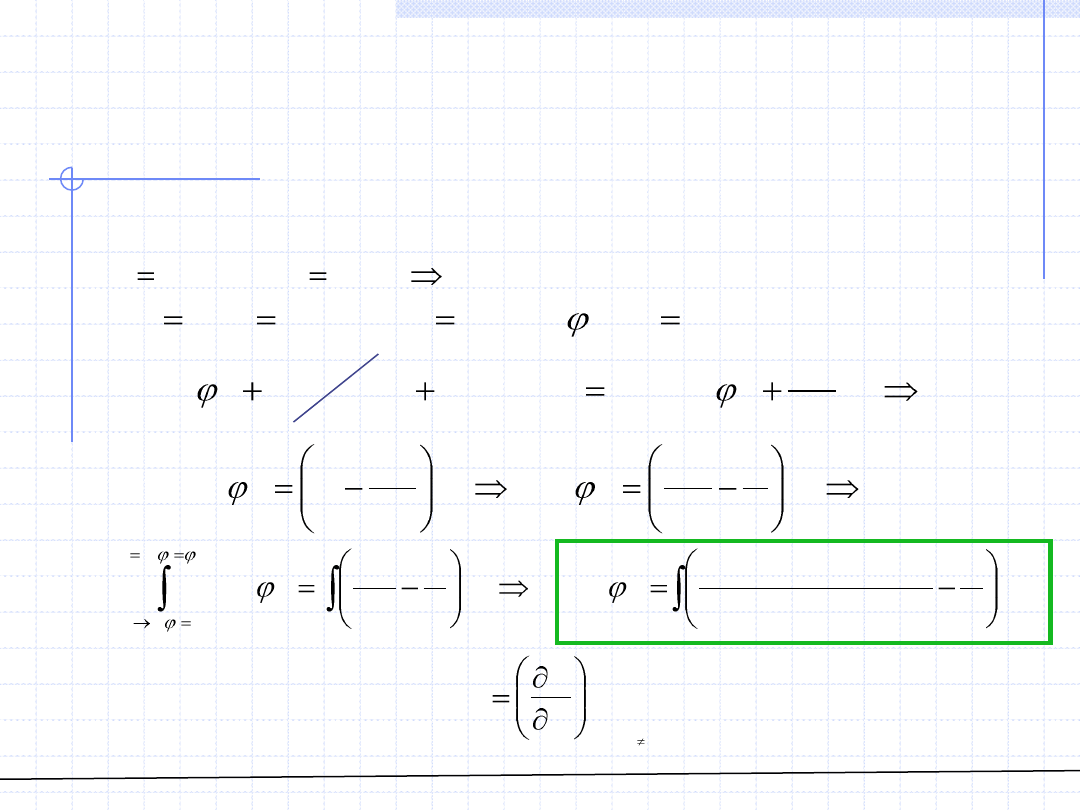
Wychodząc z definicji wyprowadzamy ważny wzór roboczy określający

współczynnik fugatywności składnika w roztworze:

.

.

const

x

const

T

i

)

ln(

)

ln(

p

x

RTd

f

RTd

dp

v

dg

i

i

i

i

i

dp

p

RT

RTd

p

RTd

x

RTd

RTd

i

i

i

)

ln(

)

ln(

)

ln(

)

ln(

dp

p

RT

v

d

dp

p

RT

v

RTd

i

i

i

i

1

)

ln(

)

ln(

p

k

i

p

p

p

p

i

i

i

dp

p

RT

x

x

x

T

p

v

dp

p

RT

v

d

i

i

i

0

2

1

,

1

,

0

0

1

)

,...,

,

,

,

(

)

ln(

1

)

ln(

i

j

n

T

p

i

k

i

n

V

x

x

x

T

p

v

gdzie

,

,

2

1

)

,...,

,

,

,

(

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY – Fugatywność

składnika w roztworze cd.

1

2

0

( , , ,

,...,

)

1

ln( )

p

i

k

i

v p T x x

x

dp

RT

p

i

j

n

T

p

i

k

i

n

V

x

x

x

T

p

v

gdzie

,

,

2

1

)

,...,

,

,

,

(

1

2

( , , ,

,..., ,...,

)

i

k

V

f p T n n

n

x

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ROZTWORY – Fugatywność

składnika w roztworze cd.

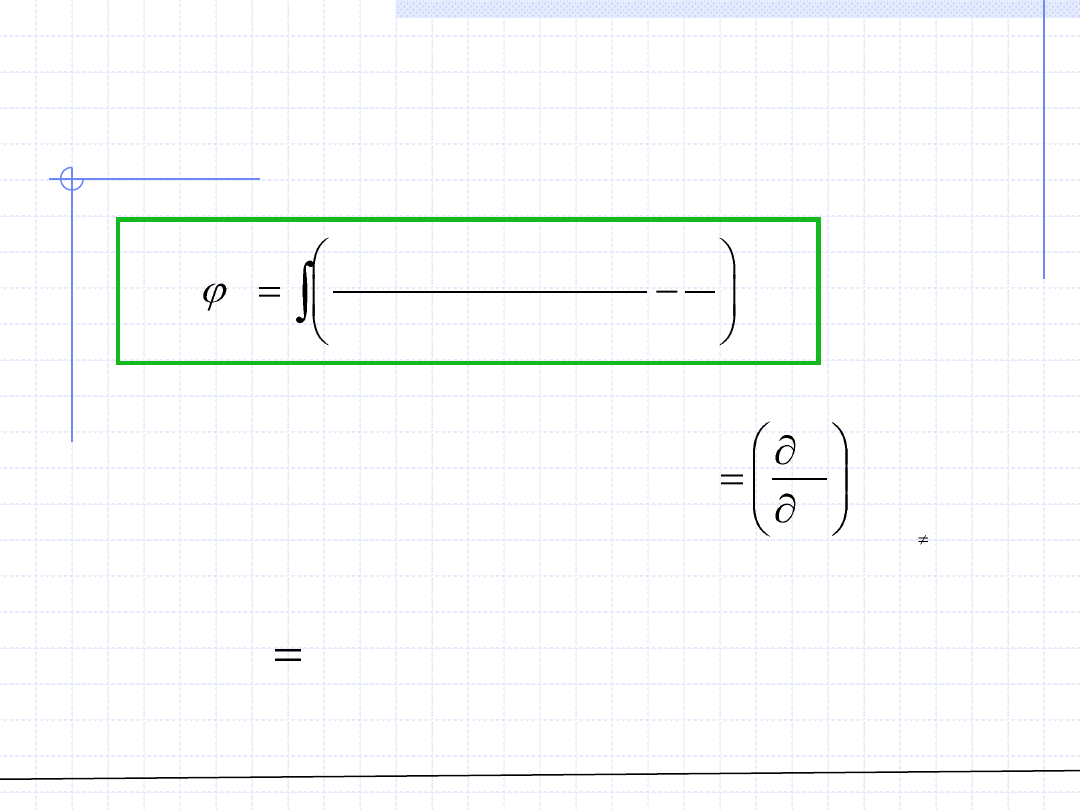
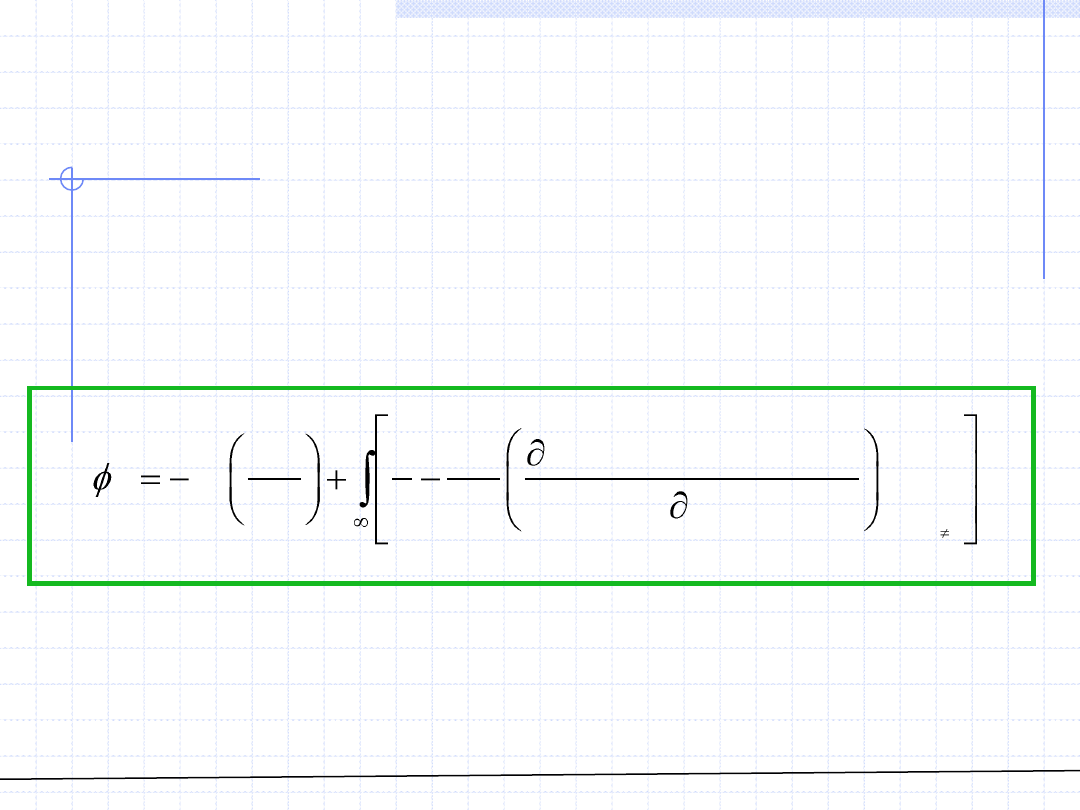
W przypadku gdy roztwór jest opisany za pomocą równania rozwiązanego

względem ciśnienia wzór całkowy określający współczynnik fugatywności

składnika w roztworze wymaga przekształcenia w celu zamiany zmiennych.

W rezultacie tego przekształcenia otrzymujemy:

1

2

, ,

( , , , ,

,...,

)

1

ln( )

ln

j i

v

k

i

i

T V n

p V n T n n

n

pv

n

dv

RT

v

RT

n

W celu zastosowania powyższego wzoru należy do równania stanu wprowadzić

objętość ogólną V oraz ułamki molowe zastąpić stosunkami liczności.

Następnie oblicza się pochodną cząstkową i z powrotem wprowadza się

objętość właściwą względem której wyznacza się całkę oznaczoną.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

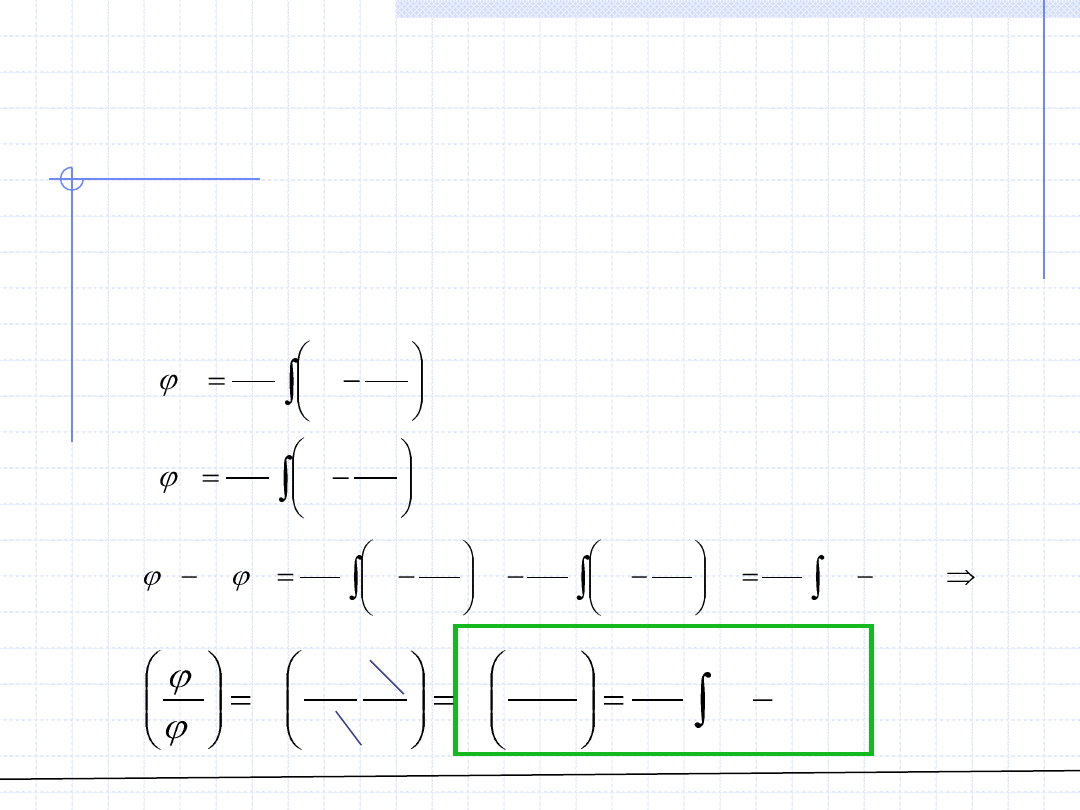
Zależność między fugatywnością składnika w

roztworze a fugatywnością czystego składnika

Fugatywność składnika w roztworze można powiązać z fugatywnością tego

samego składnika w stanie czystym pod tym samym ciśnieniem i w tej

samej temperaturze. Dla obydwu wielkości można napisać odpowiednie

wzory:

p

i

i

p

i

i

roztwór

dp

p

RT

v

RT

czysty

dp

p

RT

v

RT

0

0

0

0

1

)

ln(

1

)

ln(

p

i

i

p

i

p

i

i

i

dp

v

v

RT

dp

p

RT

v

RT

dp

p

RT

v

RT

0

0

0

0

0

0

)

(

1

1

1

)

ln(

)

ln(

p

i

i

i

i

i

i

i

i

i

i

dp

v

v

RT

f

x

f

f

p

p

x

f

0

0

0

0

0

)

(

1

ln

ln

ln

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

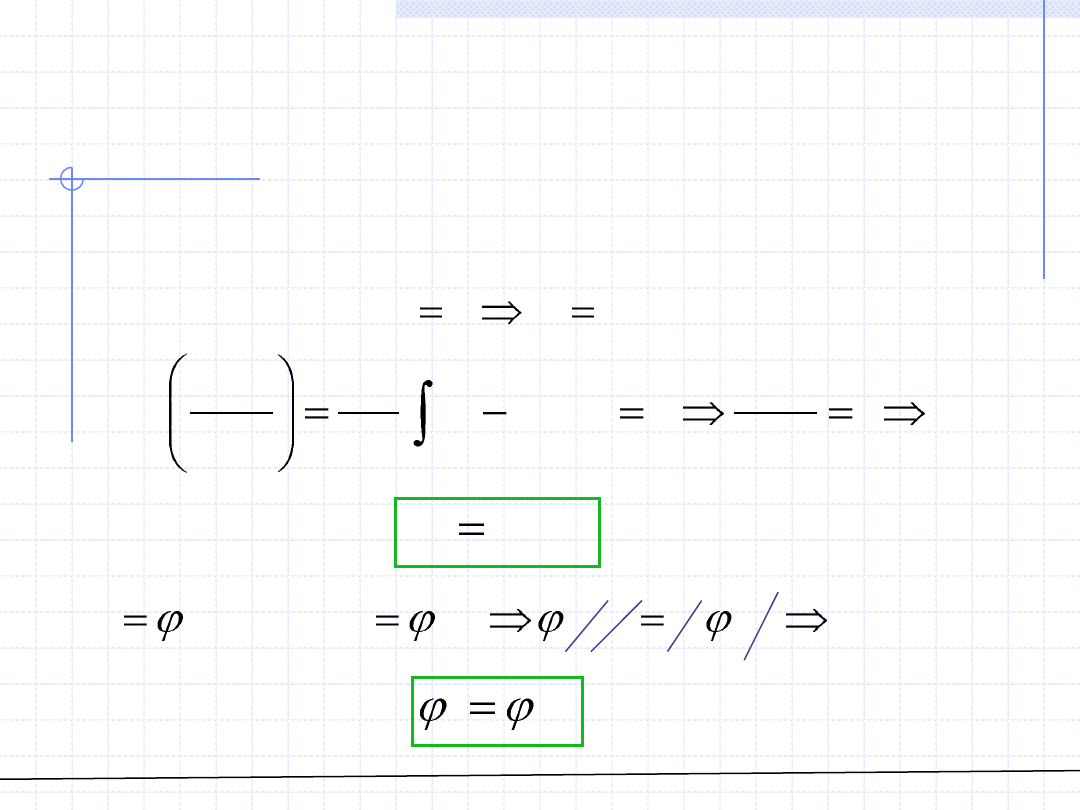
Reguła Lewisa - Randalla

Dla roztworu stosującego się do prawa Amagata obowiązuje bardzo prosta

zależność między obydwoma fugatywnościami znana jako tzw.

reguła Lewisa – Randalla:

0

0

i

i

M

v

v

V

1

0

)

(

1

ln

0

0

0

0

i

i

i

p

i

i

i

i

i

f

x

f

dp

v

v

RT

f

x

f

0

i

i

i

f

x

f

p

x

p

x

p

f

p

x

f

i

i

i

i

i

i

i

i

i

0

0

0

0

i

i

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

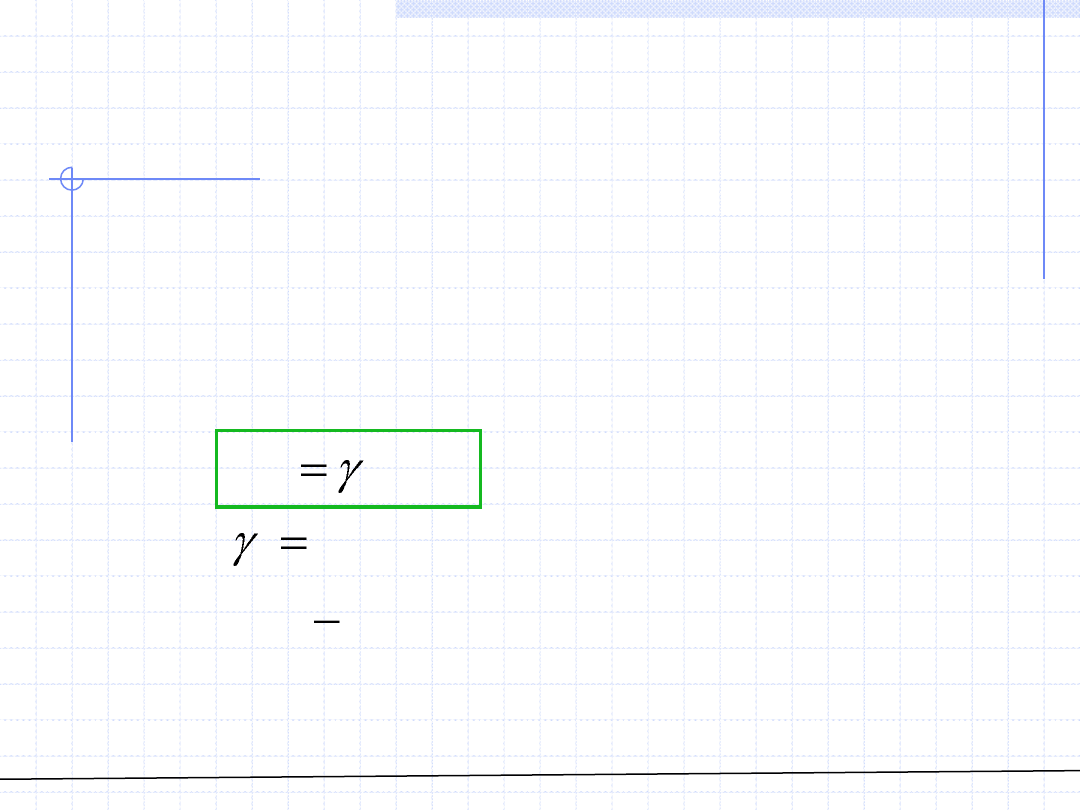
Fugatywność składnika w roztworach ciekłych

Jeżeli potrafimy opisać ciecz za pomocą równania stanu, wtedy w zasadzie

niezależnie od tego jaka to jest faza możemy korzystać z poprzednio

wyprowadzonych wzorów. Jednakże ze względu na duże trudności w takim

opisie rozwinęła się metoda opisu fugatywności w cieczy za pomocą

tzw. współczynników aktywności. Metoda ta jest powszechnie stosowana

przede wszystkim do opisu odstępstwa układów rzeczywistych od praw

opisujących roztwory idealne. Zgodnie z tą metodą fugatywność składnika

w roztworze ciekłym jest określona za pomocą wzoru:

L

i

k

i

i

L

i

i

i

L

i

f

x

x

x

T

p

f

gdzie

f

x

f

0

1

0

)

,...,

,...,

,

,

(

Współczynnik aktywności

składnika „i” w roztworze

Fugatywność czystego składnika „i” w fazie ciekłej pod tym

samym ciśnieniem i w tej samej temperaturze. Wzór

określający tą wielkość wyprowadziliśmy wcześniej.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

Fugatywność składnika w roztworach ciekłych

cd.

Poyntinga

czynnik

RT

p

p

v

Po

gdzie

Po

p

f

n

i

L

i

i

i

n

i

V

n

i

L

i

0

,

0

0

0

0

,

0

,

0

(

exp

)

(

)

(

Czynnik Poyntinga uwzględnia wpływ ciśnienia na fugatywność czystej cieczy.

Często przyjmuje się wartość tego czynnika równą 1.

Wartość z kolei współczynnika fugatywności pary nasyconej można albo

przyjmować równą 1 (dla niskich wartości p

n

) albo obliczać na postawie

równania wirialnego lub innych równań stanu.

Kluczową wielkością jest współczynnik aktywności, którego obliczanie jest

osobnym zagadnieniem. Porównując wzór definicyjny z regułą Lewisa – Randalla

możemy zauważyć, że w przypadku roztworów idealnych współczynniki aktywności

wszystkich składników muszą być równe 1.

k

i

RI

i

,...,

2

,

1

1

)

(

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

32

Na tym kończymy dzisiejszy

wykład

Dziękuję bardzo Państwu za

uwagę !

Z okazji zbliżających się Świąt

oraz Nowego 2014 Roku

składam Państwu serdeczne

życzenia wszystkiego najlepszego

!!!