© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

1

TERMODYNAMIKA

PROCESOWA I TECHNICZNA

Wykład XIII

Równowaga ciecz – para w układach

dwuskładnikowych

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

2

Równowaga fazowa w układach

dwuskładnikowych

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

3

Uwagi ogólne

Stosunkowo prosto równowagę fazową można opisać w przypadku układów

dwuskładnikowych (binarnych). W układach takich liczba stopni swobody wynosi

zgodnie z regułą faz:

s=k-f+2=2-2+2=2.

Równowaga w układzie jest zatem w pełni określona po ustaleniu dwu parametrów.

Parametrami tymi mogą być:

-ciśnienie – p

- temperatura – T

-skład fazy ciekłej – x

1

lub x

2

-skład fazy parowej – y

1

lub y

2

.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

4

Uwagi ogólne

W praktyce często rozpatrywane są sytuacje procesów izotermiczych (T=const.)

lub izobarycznych (p=const.).

Równowaga fazowa w układach binarnych jest chętnie rozpatrywana na

wykresach

zależności różnych parametrów od składu wyrażonego za pomocą ułamków

molowych. Skład taki w bardzo prosty sposób jest interpretowany za pomocą

przedziału liczb rzeczywistych [0,1].

Wartość x jest przyjmowana jako ułamek molowy składnika 1 czyli x=x

1

.

Ułamek molowy drugiego składnika x

2

=1-x

1

=1-x jest odległością danego punktu

od punktu x=1. W takiej interpretacji odcięta x=0 reprezentuje czysty składnik 1

a odcięta x=0 czysty składnik 2.

Oś odciętych może reprezentować skład fazy ciekłej, skład fazy parowej

lub jednocześnie obydwa składy.

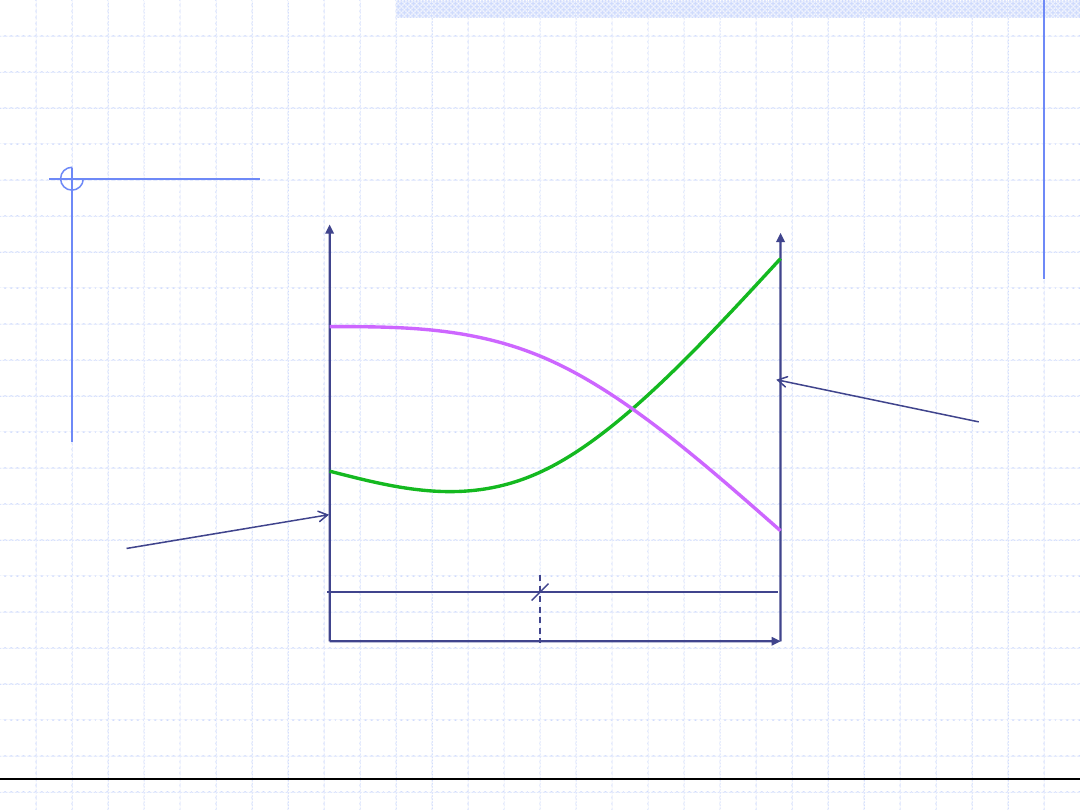
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

5

Wykresy dla układów binarnych

x=x

1

=0

y=y

1

=0

1-x=1-x

1

=x

2

=1

1-y=1-y

1

=y

2

=1

x=x

1

=1

y=y

1

=1

1-x=1-x

1

=x

2

=0

1-y=1-y

1

=y

2

=0

Dowolny parametr Y

Y(y)

Y(x)

Y

1

0V

Y

1

0L

Y

2

0L

Y

2

0V

x

1

=x

x

2

=1-x

Czysty składnik 2

Czysty składnik 1

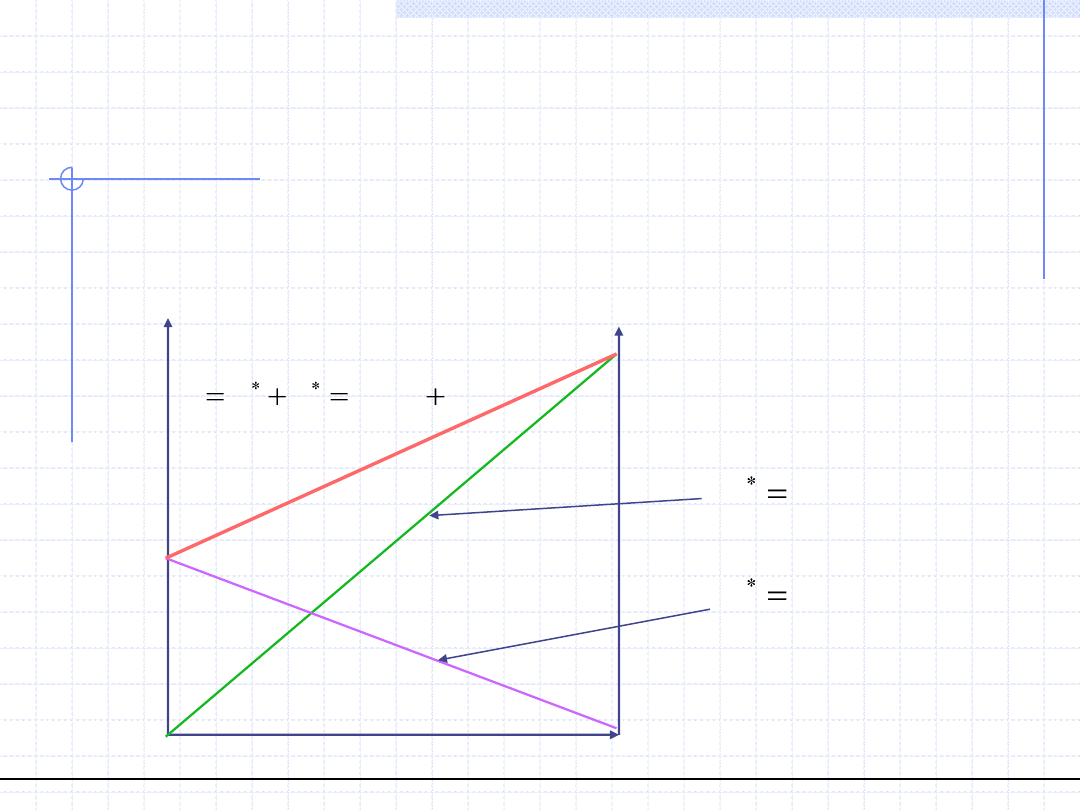
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

6

Wykresy równowagowe dla binarnych

układów izotermicznych (T=const.)

0

,

2 n

p

0

,

1 n

p

1

0

,

1

1

x

p

p

n

x=x

1

=0

x=x

1

=1

Ciśnienie cząstkowe p

1

,p

2

i ogólne p

Zakładając, że układ stosuje się do prawa Raoulta wykres równowagowy

ma szczególnie prostą postać:

2

0

,

2

1

0

,

1

2

1

x

p

x

p

p

p

p

n

n

2

0

,

2

2

x

p

p

n

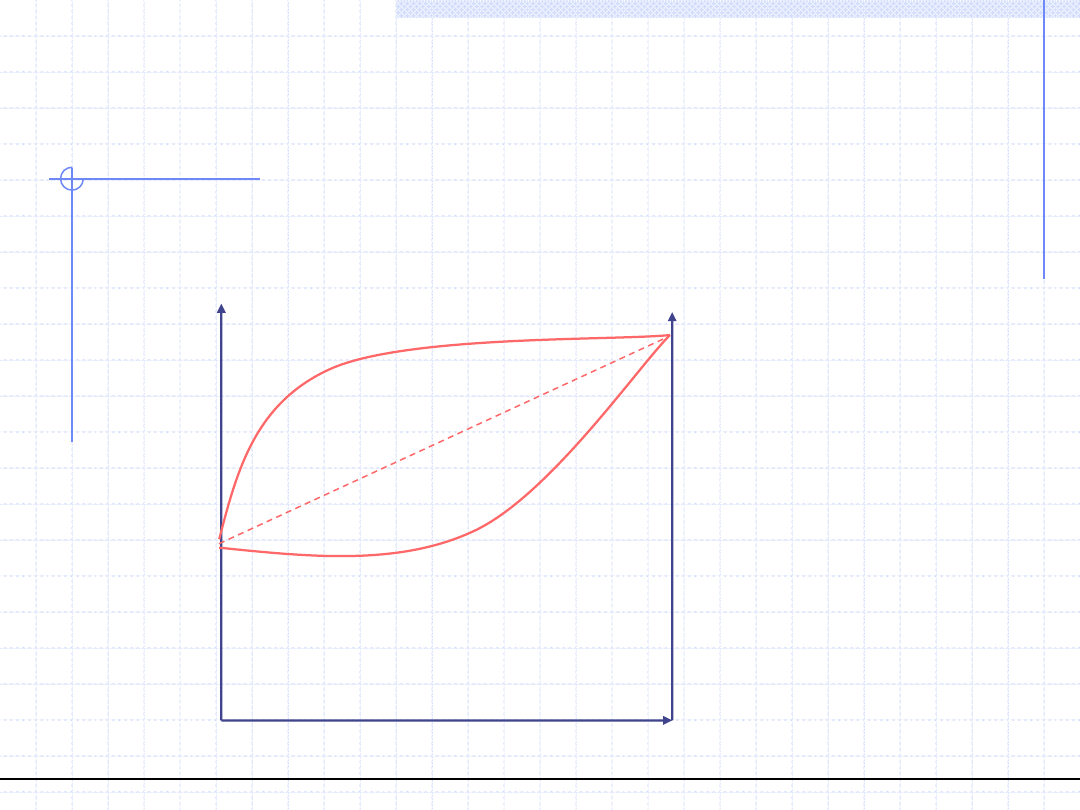
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

7

Wykresy równowagowe dla binarnych

układów izotermicznych (T=const.)

0

,

2 n

p

0

,

1 n

p

x=x

1

=0

x=x

1

=1

Na ogół rzeczywiste układy nie stosują się do prawa Raoulta.

Generalnie układy rzeczywiste mają dodatnie lub ujemne odchylenia od

prawa Raoulta. Odchylenia dodatnie są w przypadkach gdy rzeczywiste

ciśnienie w układzie jest wyższe niż ciśnienie wynikające z prawa Raoulta.

Ujemne odchylenia mamy w przypadku gdy rzeczywiste ciśnienie jest

niższe niż wynikające z prawa Raoulta. Na wykresie p – x wygląda to tak:

Odchylenia dodatnie

Odchylenia ujemne

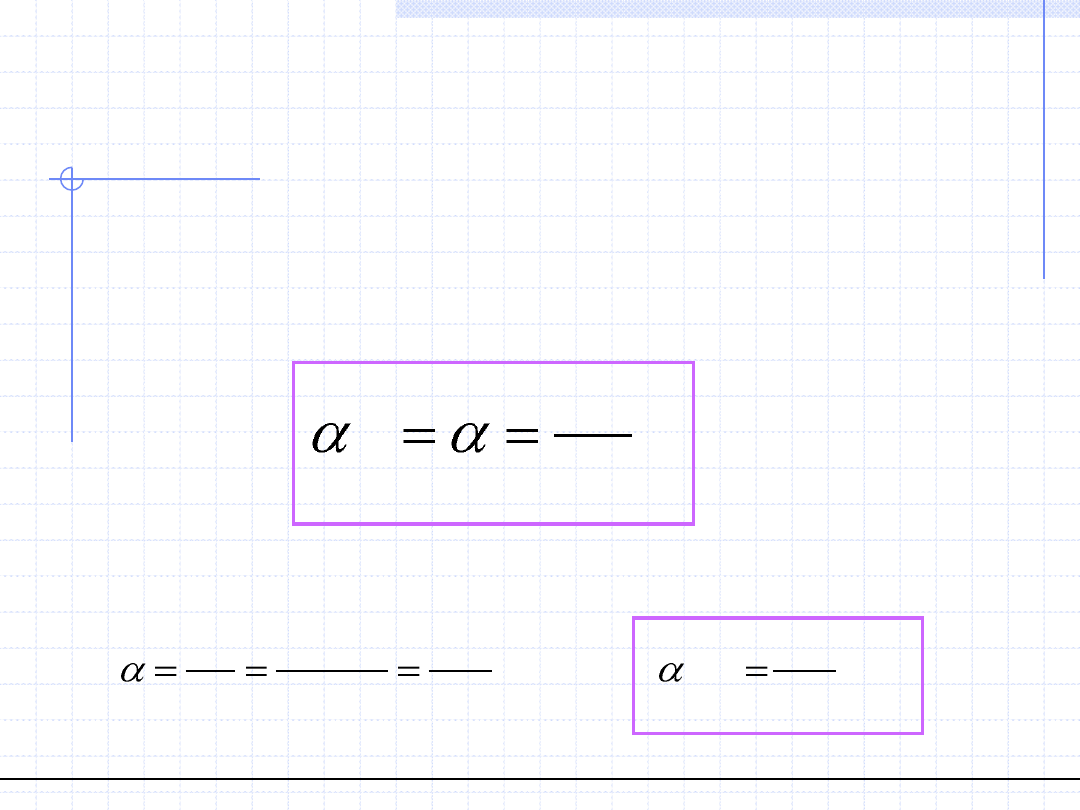
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

8

Współczynnik względnej lotności

2

1

12

K

K

W destylacyjnych układach dwuskładnikowych przy opisie stanów równowagi

stosowany jest tzw. współczynnik względnej lotności α. Definicja tego
współczynnika wymaga wyboru jednego ze składników jako punktu odniesienia.

Najczęściej wybierany jest składnik 2 mniej lotny tzn. posiadający wyższą

temperaturę wrzenia.

Współczynnik względnej lotności jest to stosunek stałej równowagi danego

składnika do stałej równowagi wybranego wzorca. Dla składnika 1 mamy:

W przypadku układów stosujących się do prawa Raoulta wartość współczynnika

względnej lotności zależy tylko od temperatury i wynosi:

0

,

2

0

,

1

)

(

0

,

2

0

,

1

0

,

2

0

,

1

2

1

/

/

n

n

PR

n

n

n

n

p

p

p

p

p

p

p

p

K

K

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

9

Współczynnik względnej lotności cd.

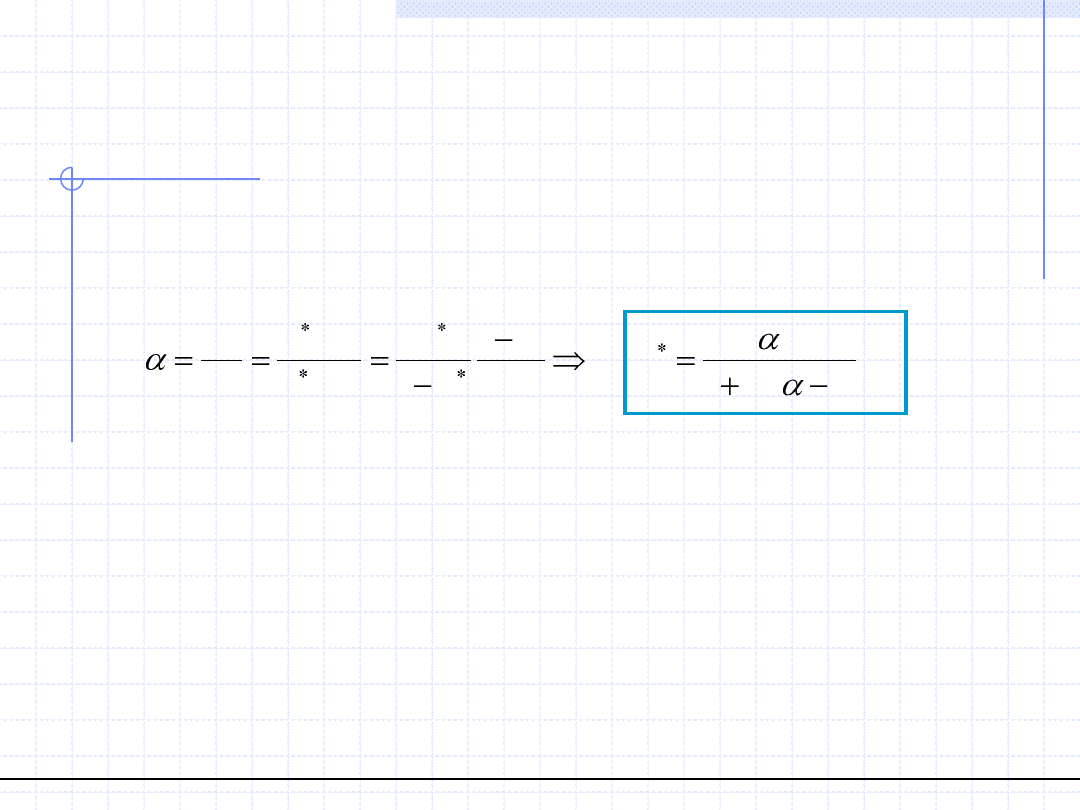
Znajomość współczynnika względnej lotności dla układu binarnego pozwala

na wyznaczenie linii równowagi w całym zakresie stężeń:

)

1

(

1

1

1

/

/

1

1

1

1

1

1

1

2

2

1

1

2

1

x

x

y

x

x

y

y

x

y

x

y

K

K

Otrzymane równanie przedstawia linię równowagi w binarnym układzie

destylacyjnym i nosi nazwę równania Fenskego. Parametrem w tym równaniu

jest wsp. α.
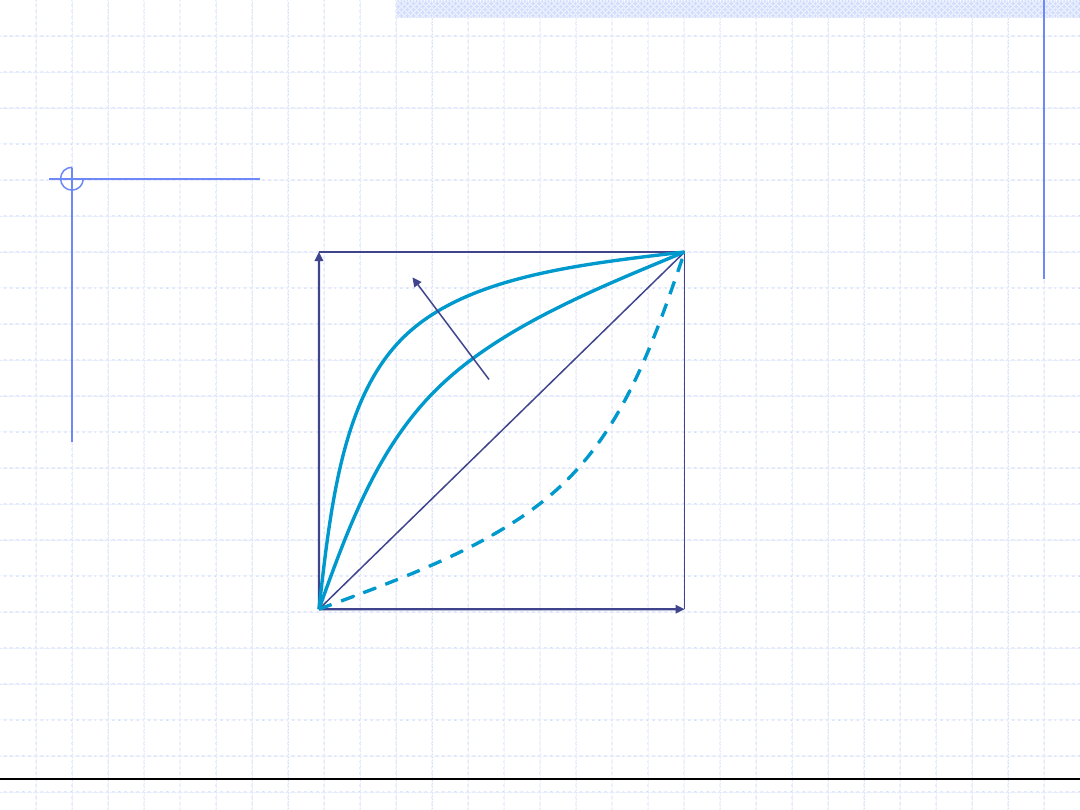
Linię równowagi w układach destylacyjnych tzn. funkcję y

*

=f(x) często rysuje

się w kwadracie jednostkowym:

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

10

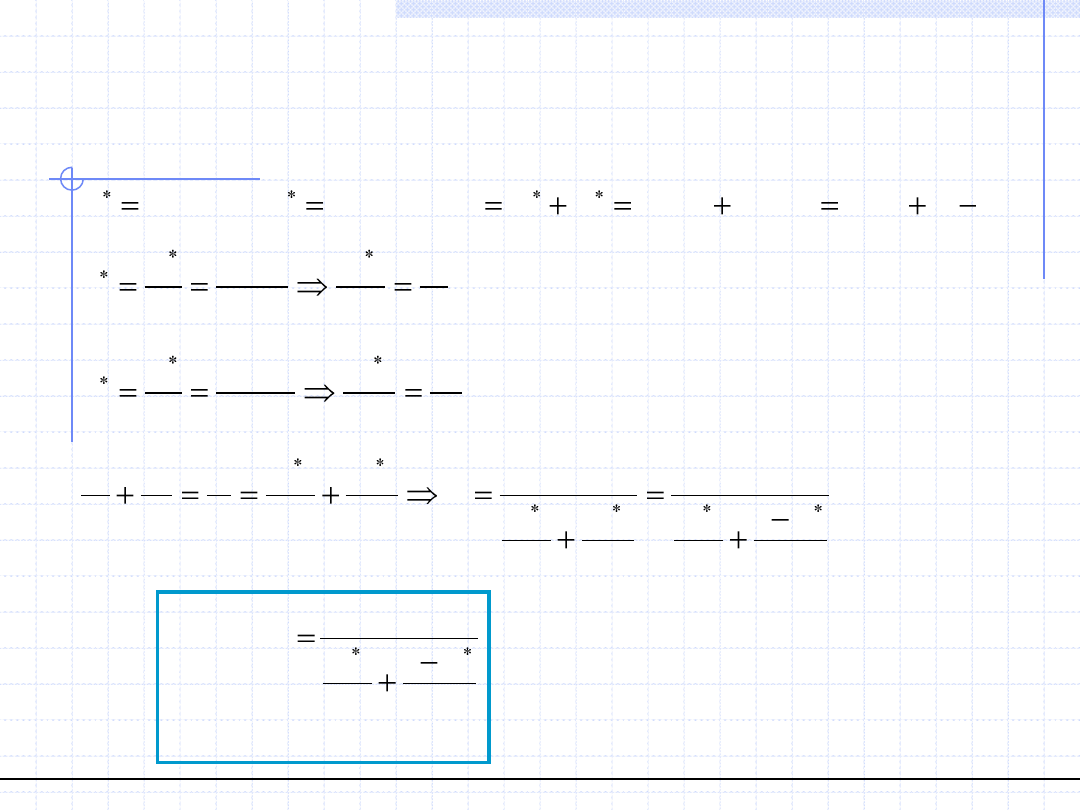
Linia równowagi w binarnym układzie

destylacyjnym x - y

x

1

=x

y

1

*

=y

α>1

α<1

T=const., prawo Raoulta => α=const.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

11

Zależność ciśnienia od składu fazy

parowej dla układów stosujących się do

prawa Raoulta

0

0

0

0

0

0

1

1

1,

2

2

2,

1

2

1

1,

2

2,

1,

2,

0

1

1,

1

1

1

1

0

1,

0

2

2,

2

2

2

2

0

2,

1

2

1

2

0

0

1

2

1,

2,

0

0

0

0

1,

2,

1,

2,

*

(1

)

1

1

1

1

1

(

)

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

p

x p

p

x p

p

p

p

x p

x p

xp

x p

x p

p

y

x

y

p

p

p

p

x p

p

y

x

y

p

p

p

p

x

x

y

y

p

y

y

y

y

p

p

p

p

p

p

p

p

p

p y

0

0

1,

2,

1

n

n

y

y

p

p

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

12

Wykresy równowagowe p – (x,y)

dla T=const.

0

,

2 n

p

0

,

1 n

p

x=x

1

=0

y=y

1

=0

x=x

1

=1

y=y

1

=1

p=x

1

p

1

0

+x

2

p

2

0

(prawo Raoulta)

p=f(x

1

), (dodatnie

odchylenie od pr. R.)

p=1/(y

1

/p

1

0

+y

2

/p

2

0

)

(prawo Raoulta)

p=f(y

1

), (dodatnie

odchylenie od pr. R.)

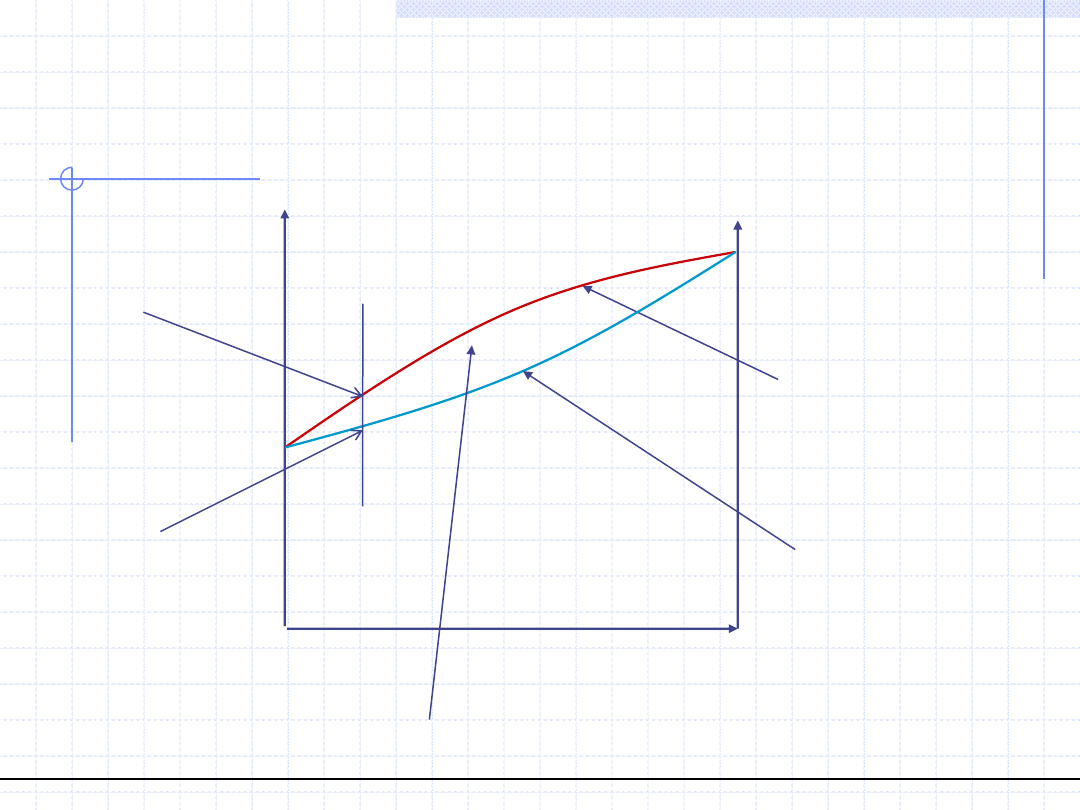
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

13

Wykresy równowagowe p – (x,y)

dla T=const.

0

,

2 n

p

0

,

1 n

p

x=x

1

=0

y=y

1

=0

x=x

1

=1

y=y

1

=1

Ciecz przechłodzona

Para przegrzana

p=f(x

1

), (dodatnie

odchylenie od pr. R.)

p=f(y

1

), (dodatnie

odchylenie od pr. R.)

Obszar dwufazowy (ciecz nasycona + para nasycona)

Ciśnienie, przy którym

skrapla się para o składzie y

Ciśnienie, przy którym wrze

ciecz o składzie x=y

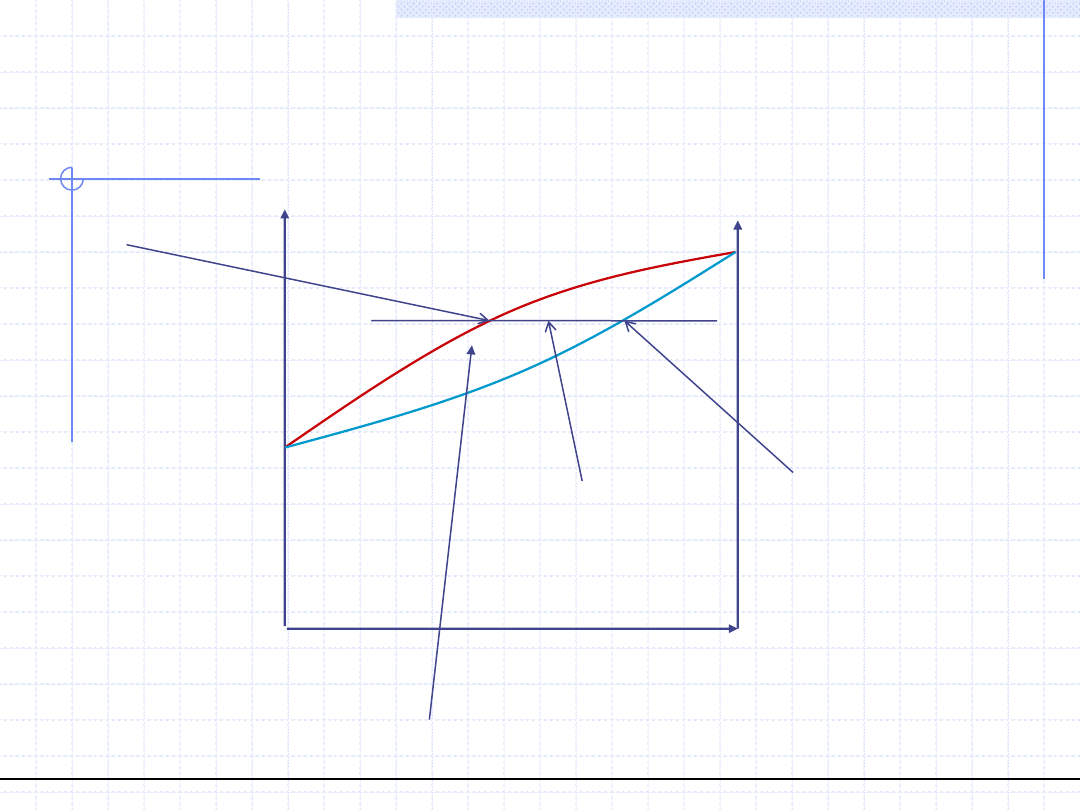
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

14

Wykresy równowagowe p – (x,y)

dla T=const.

0

,

2 n

p

0

,

1 n

p

x=x

1

=0

y=y

1

=0

x=x

1

=1

y=y

1

=1

Ciecz przechłodzona

Para przegrzana

Obszar dwufazowy (ciecz nasycona + para nasycona)

Punkt skraplania

pary przy ciśnieniu p

Punkt wrzenia cieczy przy

ciśnieniu p

y

*

>x, K>1, α>1

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

15

Układy azeotropowe

Krzywa p(x) dla układów z odchyleniami od prawa Raoulta może przebiegać

w różny sposób. W szczególności może ona wykazywać ekstrema:

maksimum dla odchyleń dodatnich i minimum dla odchyleń ujemnych.

Układ, w którym występuje ekstremum nazywamy układem azeotropowym

a konkretny skład roztworu, w którym mamy ekstremum składem

azeotropowym. Zgodnie z rodzajem odchyleń od prawa Raoulta mamy

azeotropy dodatnie i ujemne.

Fundamentalna o ogromnym znaczeniu własność roztworów azeotropowych

dotyczy stałej równowagi w punkcie azeotropowym.

Można wykazać że w punkcie azeotropowym układu dwuskładnikowego

stała równowagi obydwu składników wynosi 1 co oznacza że skład

równowagowy fazy parowej jest taki sam jak skład cieczy.

Z powyższego faktu wynika, że roztworu o składzie azeotropowym nie można

rozdzielić za pomocą destylacji.

)

(

1

1

)

(

0

2

2

2

1

1

1

1

1

a

a

a

x

y

x

y

K

x

y

K

x

x

dx

dp

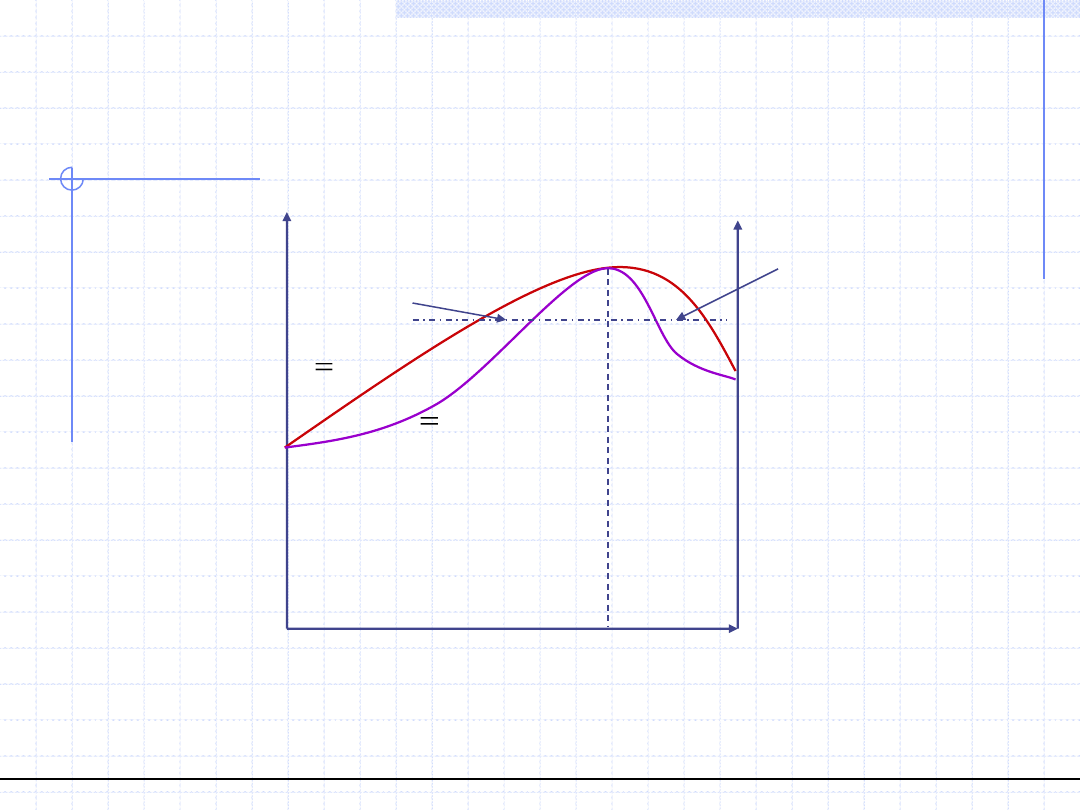
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

16

Wykresy równowagowe p – (x,y) dla

układów azeotropowych (T=const.)

)

(x

f

p

0

,

2 n

p

0

,

1 n

p

x=x

1

=0

y=y

1

=0

x=x

1

=1

y=y

1

=1

x

1

=x

a

)

( y

f

p

y

*

>x, K>1

y*<x, K<1

Dodatnie odchylenia od prawa Raoulta

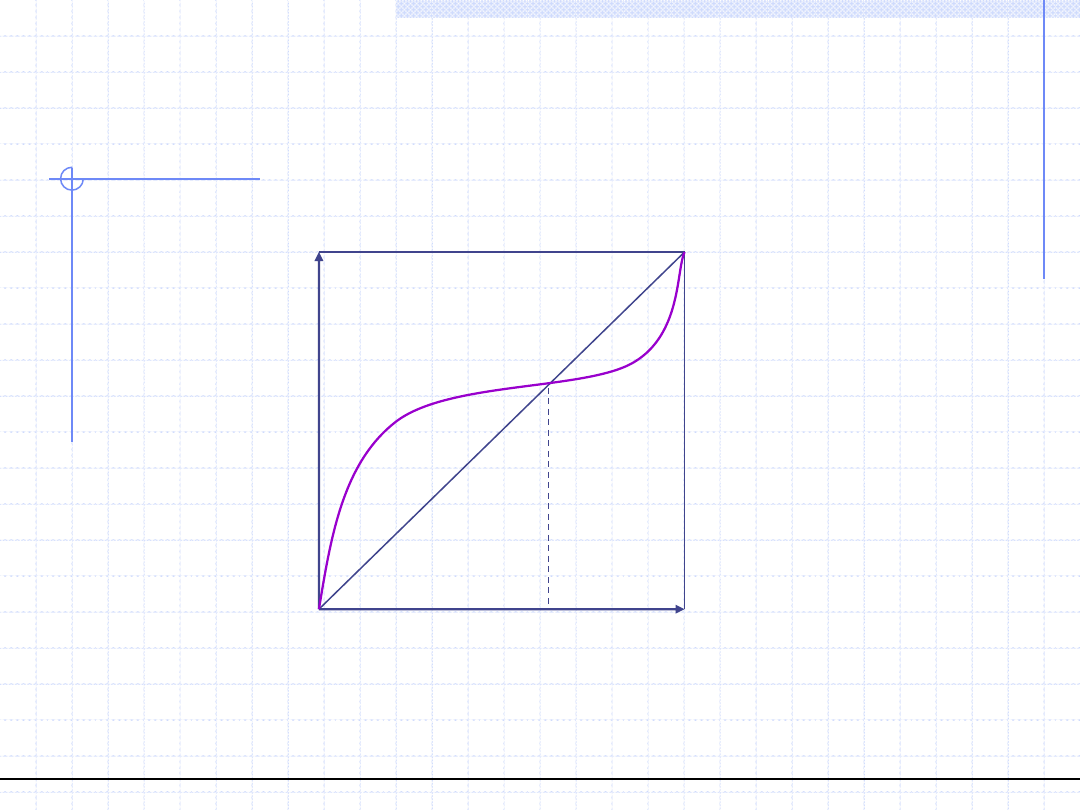
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

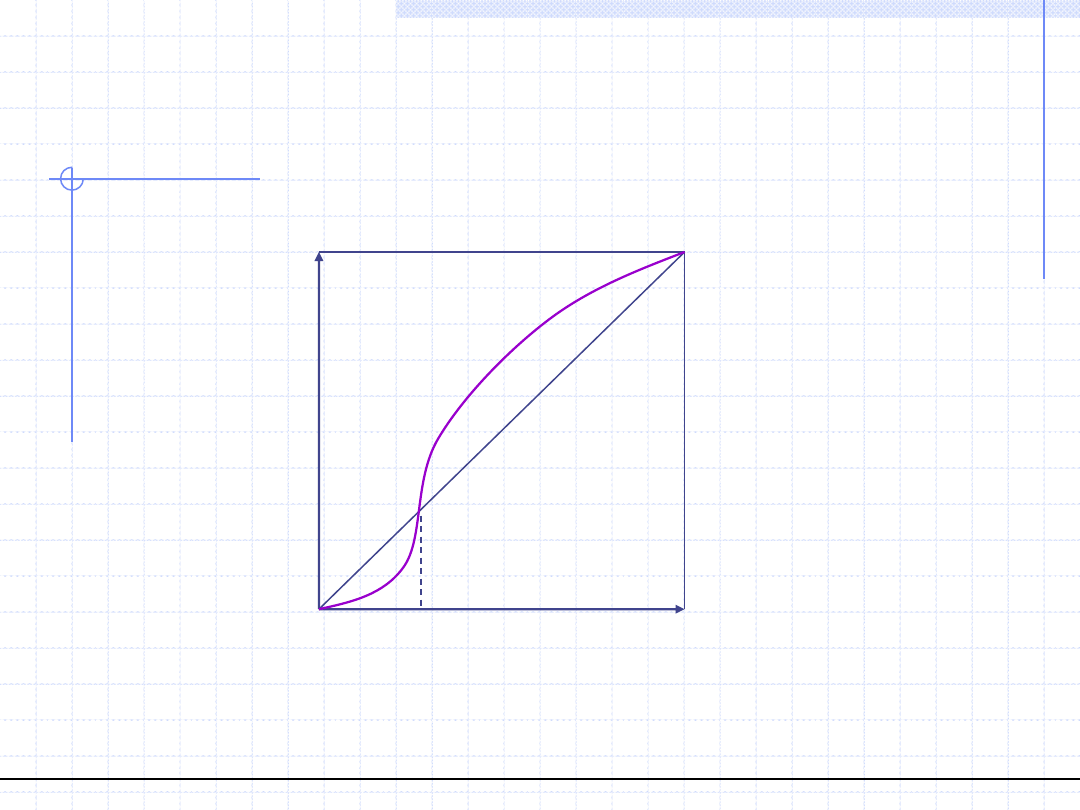
17

Wykres równowagowy y – x dla

układów azeotropowych (T=const.)

x

1

=x

y

1

*

=y

x

1

=x

a

=y

a

Azeotrop dodatni

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

18

Wykresy równowagowe p – (x,y) dla

układów azeotropowych (T=const.)

)

(x

f

p

0

,

2 n

p

0

,

1 n

p

x=x

1

=0

y=y

1

=0

x=x

1

=1

y=y

1

=1

x

1

=x

a

)

( y

f

p

y

*

<x, K<1

y*>x, K>1

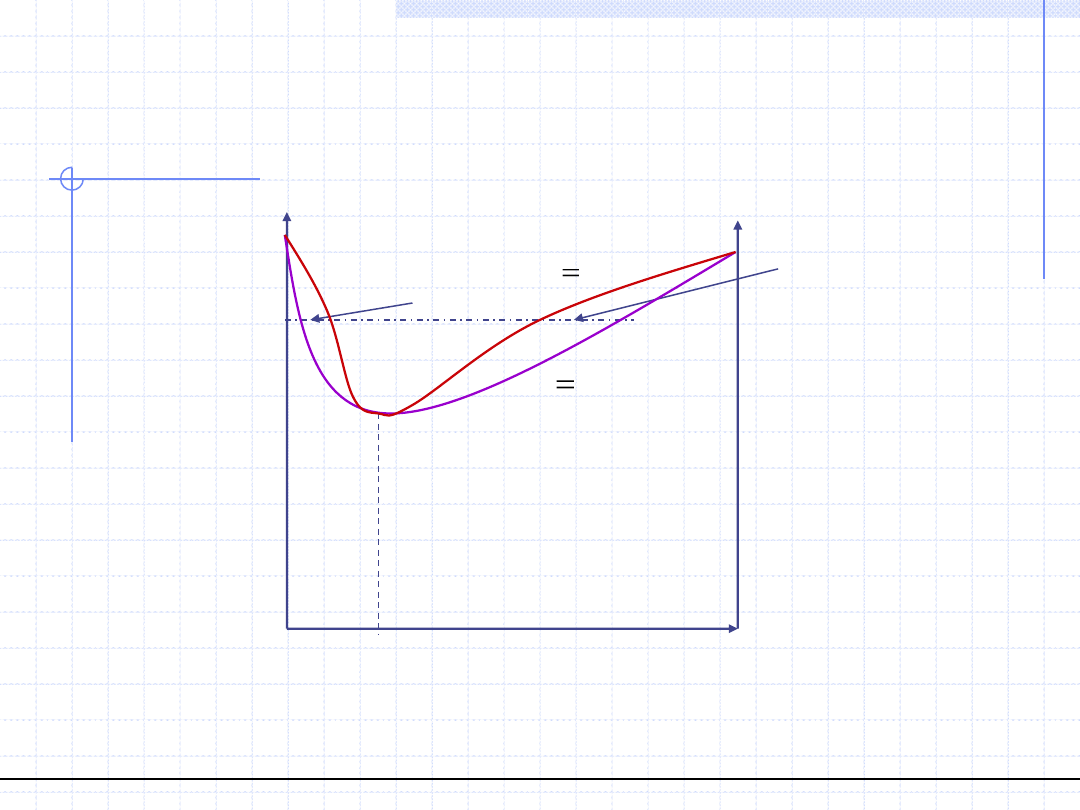
Ujemne odchylenia od prawa Raoulta

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

19

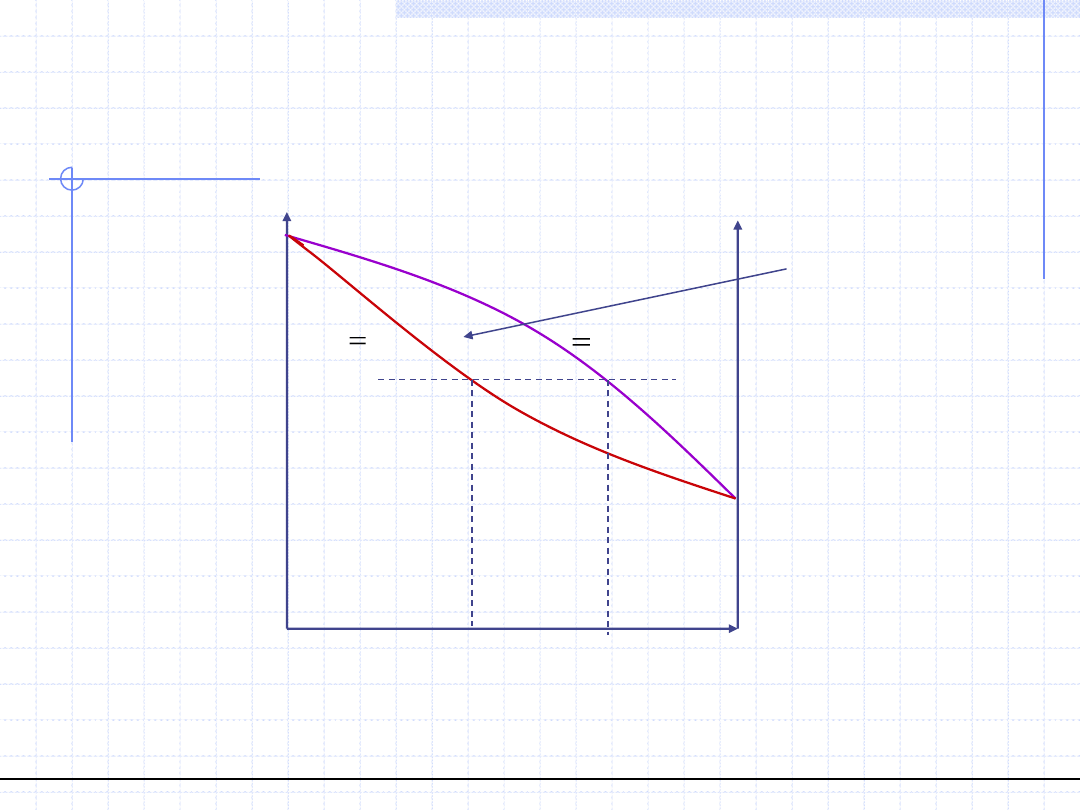
Wykres równowagowy y – x dla

układów azeotropowych (T=const.)

x

1

=x

y

1

*

=y

x

1

=x

a

=y

a

Azeotrop ujemny

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

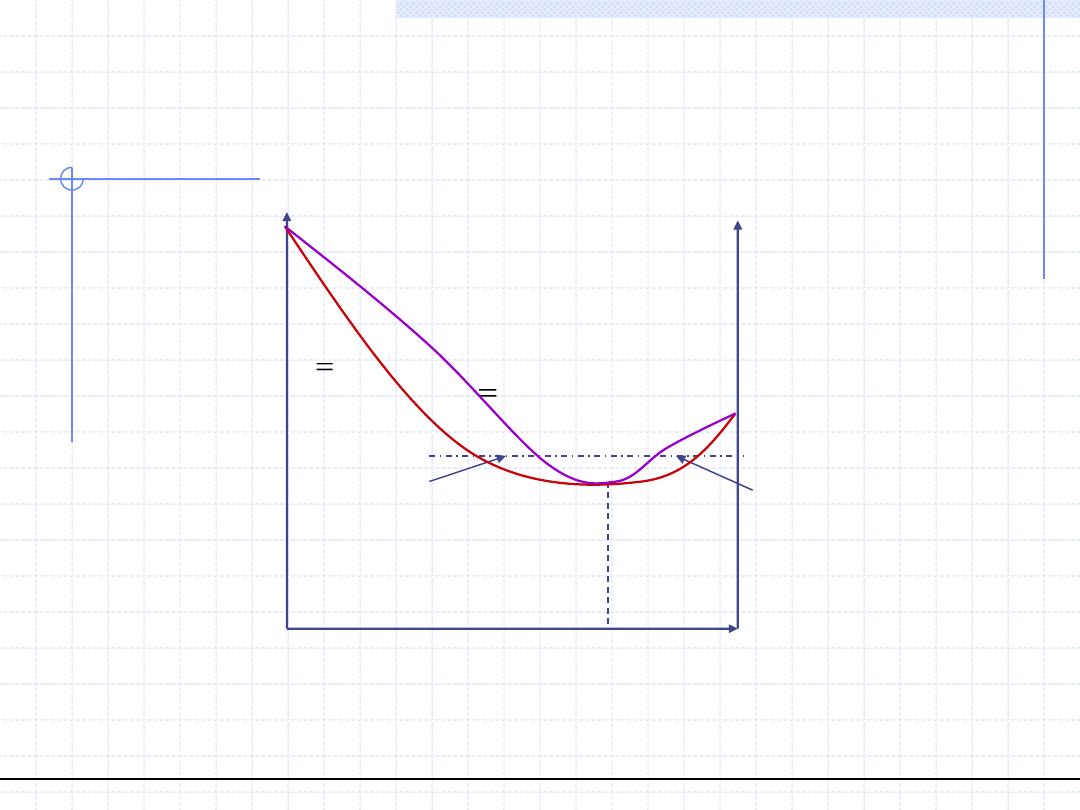
20

Wykresy równowagowe T – (x,y)

(p=const.)

)

(x

f

T

0

.

,

2 wrz

T

0

.

,

1 wrz

T

x=x

1

=0

y=y

1

=0

x=x

1

=1

y=y

1

=1

)

( y

f

T

x

1

=x

y

*

Ciecz przechłodzona

Para przegrzana

Ciecz nasycona +

para nasycona

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

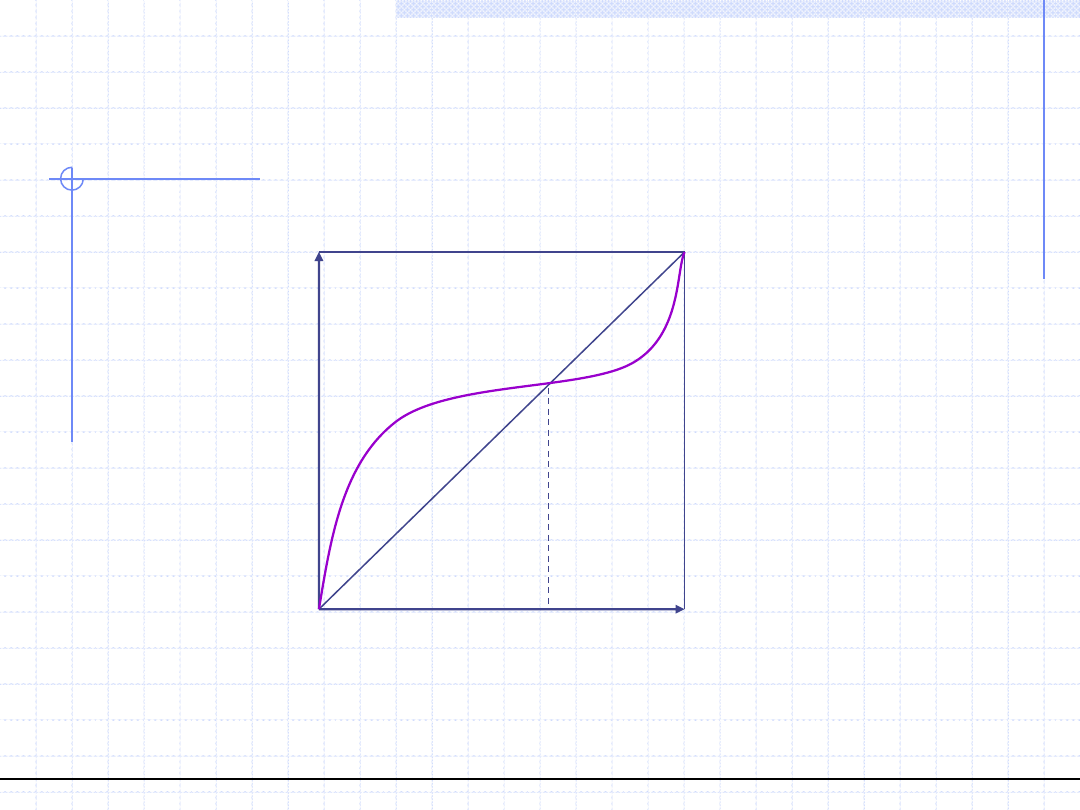
21

Wykresy równowagowe T – (x,y) dla

układów azeotropowych (p=const.)

)

(x

f

T

0

.

,

2 wrz

T

0

.

,

1 wrz

T

x=x

1

=0

y=y

1

=0

x=x

1

=1

y=y

1

=1

x

1

=x

a

)

( y

f

T

y

*

>x, K>1, α>1

y*<x, K<1, α<1

Dodatnie odchylenia od prawa Raoulta

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

22

Wykres równowagowy y – x dla

układów azeotropowych (p=const.)

x

1

=x

y

1

*

=y

x

1

=x

a

=y

a

Azeotrop dodatni

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

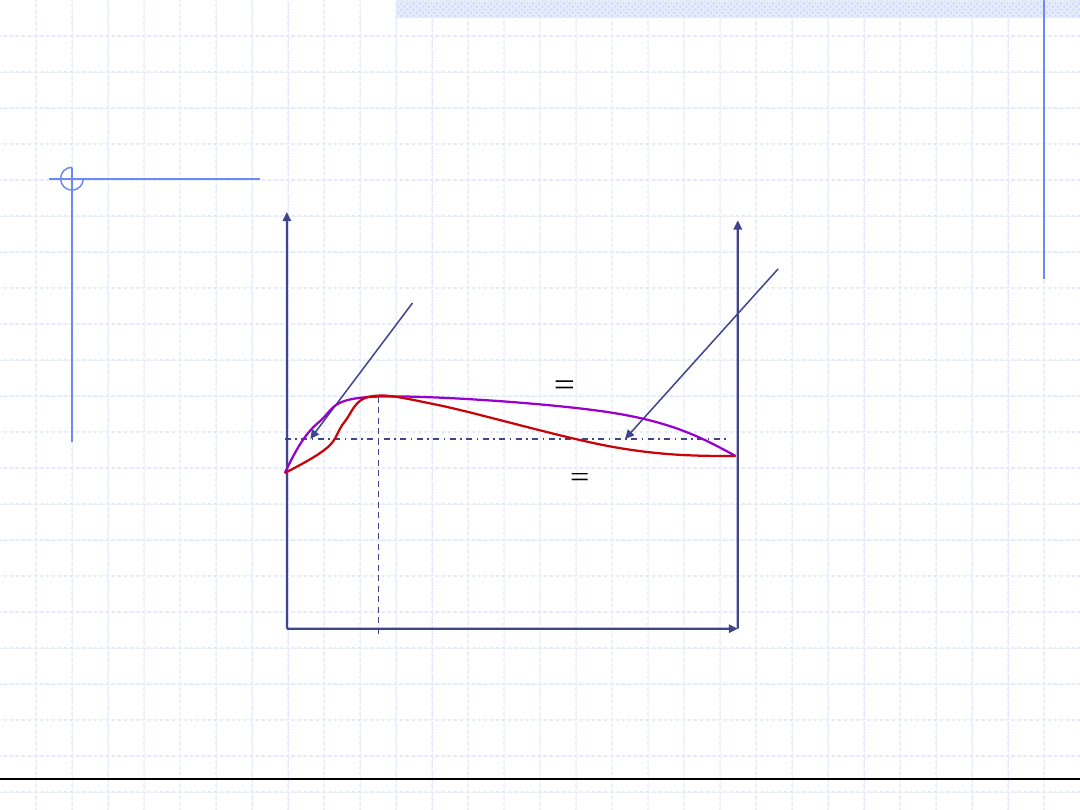
23

Wykresy równowagowe T – (x,y) dla

układów azeotropowych (p=const.)

)

(x

f

T

0

.

,

2 wrz

T

0

.

,

1 wrz

T

x=x

1

=0

y=y

1

=0

x=x

1

=1

y=y

1

=1

x

1

=x

a

)

( y

f

T

y

*

<x, K<1, α<1

y*>x, K>1, α>1

Ujemne odchylenia od prawa Raoulta

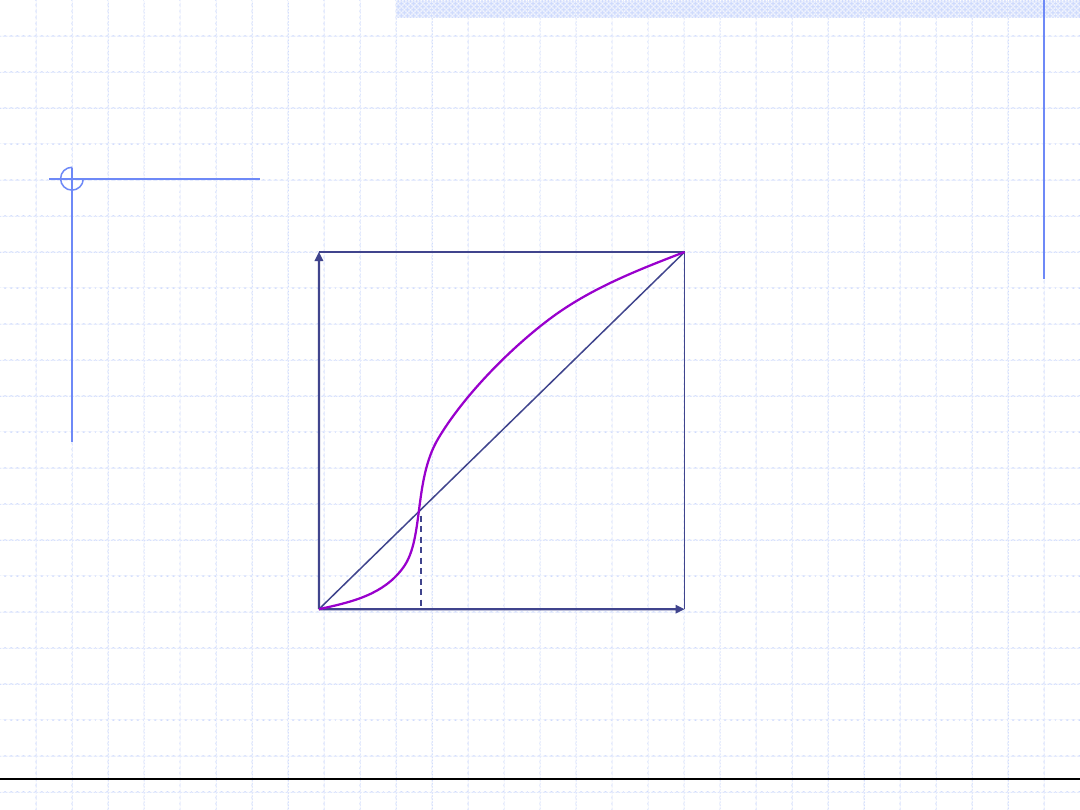
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

24

Wykres równowagowy y – x dla

układów azeotropowych (p=const.)

x

1

=x

y

1

*

=y

x

1

=x

a

=y

a

Azeotrop ujemny

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

25

Na tym kończymy wykłady z „Termodynamiki

procesowej i technicznej”. Dziękuję bardzo Państwu

za uwagę i życzę powodzenia na egzaminie,

który odbędzie się:

27.01.2014 godz. 10.15 – 12.00 s. B1 F4 termin „0”

07.02.2014 godz. 8.00 - 10.00 s. 310 A2 I termin

17.02.2014 godz. 9.00 – 11.00 s. B1 F4 II termin